影响不对称支撑圆形钢天线风致疲劳寿命的因素

王钦华,顾 明

(1.同济大学土木工程防灾国家重点实验室,上海 200092;2.汕头大学 土木工程系,广东 汕头 515063）

对于轻质、柔性结构,风荷载是其主要的控制荷载,结构在风荷载的作用下产生较大幅度的振动,而结构在经历了大量的应力循环后,易发生风振疲劳破坏。风振疲劳破坏的例子较多[1-7],但是对于风振疲劳研究的文献较少。Gu等[8]对上海地区的气象资料进行统计分析得到了该地区风速风向联合分布函数,并对杨浦大桥进行抖振响应分析,得到每个风向角各个风速下钢箱梁关键点处的应力功率谱密度函数,用蒙特卡洛方法模拟了关键点处的应力时程,然后用雨流计数法对应力时程进行计数得到应力范围的分布函数,在此基础上对杨浦大桥进行风振疲劳分析。M.Dionne和A.G.Davenport[9]建立了阵风响应因子和风振疲劳之间的关系,其文献将结构的响应分为背景响应和共振响应两部分,用Miner累积损伤理论计算结构的疲劳寿命,这个方法只能用于由顺风向力引起的疲劳问题。M.P.Repetto和G.Solari[10]将结构的应力响应分为背景响应和共振响应,用累积损伤理论对结构进行顺风向疲劳寿命分析。此后,M.P.Repetto和 G.Solari[11-13]考虑了顺风向力、横风向力以及涡激共振的影响对圆形线状结构进行风振疲劳寿命分析,但其文献中没有详细讨论风向、结构表面粗糙度以及平均风速对疲劳寿命的影响。文献[14-15]基于一钢质天线气动弹性模型风洞试验结果,分别用频域和时域的方法研究了其风致疲劳。

该文在求得结构不同风向、风速下风致响应以及结构所在位置处的风速风向联合分布函数的基础上,基于经典的疲劳累积损伤理论,对不对称支撑圆形截面钢结构进行风致疲劳寿命估计,通过实例分析的结果,详细讨论了风向、结构表面粗糙度、涡激共振以及平均风速等重要因素结构风致疲劳寿命的影响。

1 结构风致疲劳寿命分析理论

结构风致疲劳寿命的分析方法可以分为3类:第1类是时域法,其目的是从用于疲劳分析的应力时程响应中,通过雨流计数法计数得到应力范围或者应力幅值的概率密度分布函数,第2类是基于随机振动和概率论的频域方法,其目的是由应力功率谱响应通过穿越分析得到应力范围或者应力幅值的概率分布密度函数。第3类主要针对考虑背景响应不可忽略的结构风致疲劳问题,为了缩减计算量,提高计算效率,先根据随机振动理论求得用于疲劳分析的应力响应谱,再用Monte Carlo法模拟应力时程,计数后求得应力范围或者幅值的概率密度函数,Gu等[8]定义这种方法为频-时域方法。以上3类方法是基于线性疲劳累积损伤理论,其主要不足在于:损伤与荷载状态无关;累积损伤与荷载次序无关;不能考虑荷载间的相互作用。

1.1 风致疲劳寿命时域分析方法

由于结构的疲劳累积损伤与风向角和风速有关,首先要定义工况,假设每一个风向角范围[θi,θi+1]下风速范围[vj,vj+1]是第[i,j]个工况,每个工况出现的概率为pij,可以由风速风向分布联合函数求得;第[i,j]个工况下,单位时间内应力范围出现次数的数学期望为,应力范围的概率密度函数;单位时间内,第k级应力范围出现的次数为:

式中,应力范围的概率密度函数 fSij是采用雨流计数法对应力时程进行计数,根据计数结果拟合得到;单位时间内应力范围出现次数的数学期望为:

式中,nij为用雨流法计数第[i,j]个工况下的应力时程得到的应力范围的总次数;tij为第[i,j]个工况下应力时程的时间。

第[i,j]个工况下的累积损伤为:

结构在时间T内总的累积损伤为:

1.2 风致疲劳寿命频域分析方法[15-16]

对于随机平稳应力过程s(t),假设其应力幅值和峰值总数为相互独立的随机变量。如果该应力过程的应力范围分布用连续的概率密度函数表示,根据S-N曲线和疲劳累积损伤准则,疲劳累积损伤可以改成下列的连续形式:

式中,dn是在区间dS内应力范围的循环次数,它等于该区间内应力范围出现的概率 fS(S)dS和应力幅值总次数mp的乘积;m、A是与材料性质有关的常数。

第[i,j]工况下,单位时间内造成的疲劳累积损伤D0ij为:

式中,flij为第[i,j]工况下单位时间内应力范围总数的数学期望;fSLij(s)为应力范围概率密度函数。以上2个参数可以通过疲劳分析关键点处的应力功率谱密度函数而求得[13]。

T时间内由第[i,j]工况下内造成的累积损伤为:

1.3 结构风致疲劳寿命分析流程

以上简单介绍了风致疲劳寿命分析方法,该节给出进行结构风致疲劳寿命分析流程:

1)根据结构附近气象站处的风速风向实测资料,得到结构处的风速风向联合分布函数,计算每个风向风速区间出现的概率以及每个风向角下不同重现期对应的最大风速。由于在计算结构的风致疲劳寿命时,需要计算每个风速风向区间造成的疲劳累计损伤,每个风向区间下风速的最大值须根据疲劳寿命作为重现期来确定。

2)假设结构的风致疲劳寿命,根据假设的疲劳寿命计算每个风向区间要考虑的最大风速。

3)计算每个风向风速区间下,用于疲劳分析的应力响应。

4)基于疲劳累计损伤理论用时域方法或者频域方法计算结构的疲劳寿命。

5)判断假设的疲劳寿命与计算得到的疲劳寿命的差值是否满足要求,如果是,结束;如果否,返回到第2)步后循环计算,直到假设的疲劳寿命与计算得到的疲劳寿命的差值满足要求为止。

为了使结构风致疲劳寿命分析流程表述更加直观,图1给出了流程图。

图1 风振疲劳寿命分析流程图

2 实例分析

以某一位于上海的超高层建筑上的天线为实例进行分析,该高层建筑主楼高度为245 m,主楼上部天线高为87 m。天线顶端离地高度为333m。天线由下往上分段等截面,每段高度依次为34m、27 m、26 m,其直径分别为2.4m、1.75 m、1 m,壁厚各为3 cm、2.5 cm、2 cm。在距离底部34m处有一个斜支撑其直径为1 m,见图2所示。

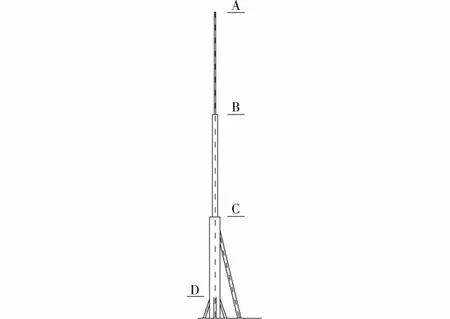
图2 天线结构图

文献[14]中给出了天线结构位置处的风速风向联合分布函数,文献[17]介绍了求解不同风向角、风速下用于疲劳寿命分析的结构响应的方法。该文用文献[17]中的方法对天线结构疲劳关键点处进行应力响应分析,结构关键点的位置见文献[14]。此外,为了考虑结构表面粗糙度对结构风致疲劳寿命的影响,根据文献[18]结构表面粗糙度ε分别选用0.002、0.0012、0.0004。以22.5度风向间隔,将0 ～ 360度风向划分为16个风向区间。不考虑斜撑对结构风场影响时,结构关于X、Y轴对称,所以只计算0～90度风向下的响应即可,有关风向角的定义如图3所示 。风速范围间隔 Δ vj=vj+1-vj为1 m/s,v00,在分析过程中以。计算了0～90度风向角、所有风速下,结构关键点处的名义应力响应,由于篇幅的限制这里只给出几个典型工况下的名义应力响应。图4给出了不同风向、风速以及结构表面粗糙度下结构的名义应力响应谱。

图3 风向角的定义

图4 不同风向、风速以及结构表面粗糙度下结构的名义应力响应谱

由图4(1)可知,在90度风向角4.5 m/s风速下,应力功率谱在0.475 Hz处出现唯一峰值,这是因为在该风向角和风速下结构发生一阶涡激共振。(2)图表明,在0度风向角6.5 m/s风速下结构发生二阶涡激共振。由(3)图可知,应力功率谱出现几个峰值,但在0.475 Hz和0.675 Hz处峰值最大,这表明在此风向角下结构的一阶和二阶阵型对结构响应的贡献较大。图4中所有的图表明在相同的风向角和风速下,结构表面粗糙度ε越大结构的响应就越大。

图5给出了不同表面粗糙度下结构的应力根方差随风速的变化规律。图5中(1)-(4)图表明不考虑涡激共振时结构的应力响应随着风速的增大而增大;结构的粗糙度ε对结构的应力响应影响较大。在相同风速条件下,粗糙度ε越大,结构的应力响应也越大。

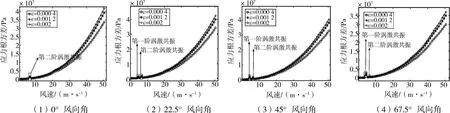
图5 不同风速风向角风速下应力根方差

在求得不同风向角、风速下结构应力响应的基础上,对结构进行风致疲劳寿命估计。在计算结构的风振疲劳寿命时,根据《钢结构设计规范》(GB50017-2003)规定,构件连接类别选为8类,其S-N曲线参数为m=3,A=4.1×1011。以下讨论了风向、结构表面粗糙度、涡激共振以及平均风速等重要因素对结构风致疲劳寿命的影响。

2.1 平均风速对疲劳寿命的影响

根据应力响应功率谱,用Monte Carlo方法模拟了应力时程响应,并用雨流法对应力时程响应进行计数,用Goodman法则考虑了平均风荷载引起的平均应力的影响,得到了应力范围出现的概率,对天线进行风致疲劳寿命估计。

当表面粗糙度为0.0012时,考虑平均风速的影响,用时域法计算得到的结构的风致疲劳寿命为116.37 a;不考虑平均风速影响,用时域方法计算得到的风致疲劳寿命为117.95 a。从中可以看出平均风速对结构风振疲劳寿命影响较小。图6-图7给出了2个典型风向角和风速下,模拟的应力时程响应,用雨流法计数应力时程并考虑平均应力影响的应力范围及其出现的次数以及应力范围在结构疲劳寿命期内的累积损伤。图6中(1)图表明90度风向角4.5 m/s风速下,结构发生一阶涡激共振的应力幅值为4 MPa左右,所以(2)图中用雨流计数法得到的接近8 MPa的应力范围(应力幅值的2倍)出现的次数最多,(3)图说明以某一阶振型振动产生的应力时程,产生疲劳累积损伤的应力范围为应力幅值的2倍。图7是考虑前5阶振型后得到的应力时程,其(3)图表明出现次数最多的小应力范围产生的疲劳累积损伤较小,而出现次数相对较少的大应力范围造成的累积损伤较大。

图6 图90度风向角4.5 m/s风速下雨流计数结果和累积损伤

图7 图45度风向角19.5 m/s风速下雨流计数结果和累积损伤

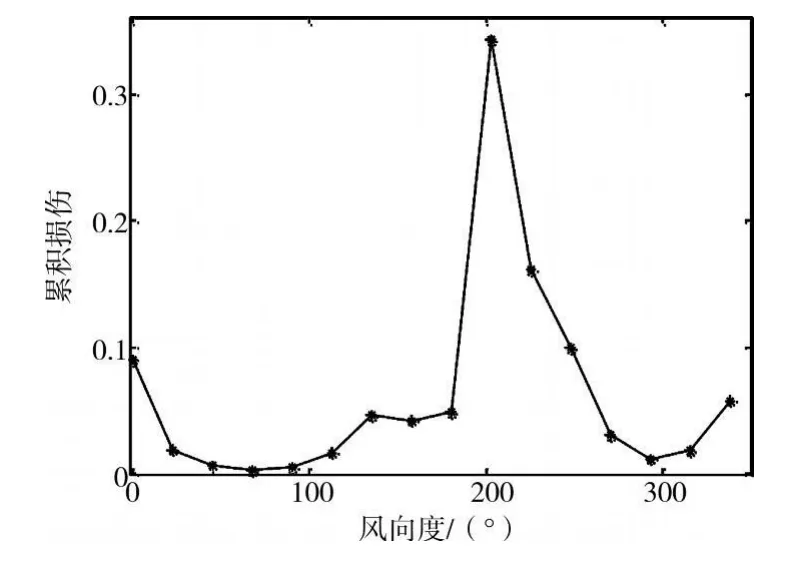
图8 考虑涡激共振时累积损伤随风向角的变化

图9 考虑涡激共振时累积损伤随风速的变化

图8和图9给出了疲劳累积损伤随风向角和风速的变化规律,从图8中可以看出风向角对疲劳累计损伤的影响较大。从图9中可以看出4.5 m/s、6.5 m/s以及20～30 m/s风速下产生的疲劳累计损伤较大,这是因为:在4.5和6.5 m/s风速下结构产生涡激共振,20～30 m/s风速下引起结构较大的应力。

2.2 结构表面粗糙度对疲劳寿命的影响

表面粗糙度分别为0.0004、0.0012以及0.002时,用频域法计算得到的结构风致寿命分别为142.57 a、101.54 a以及 91.62 a。由此可见,结构表面粗糙度对圆形单体结构的风致疲劳寿命影响很大,结构的疲劳寿命随着表面粗糙度的增加而减小。这是因为当雷诺数大于4×104时,结构表面粗糙度对结构的阻力系数影响很大,阻力系数随着结构表面粗糙度的增加而增大,因此结构的应力响应随着结构表面粗糙度的增加而增大。图10给出了风速风向区间出现的概率。图11给出了结构表面粗糙度参数为0.0004、0.0012以及0.002时,各个风速风向工况下的风致疲劳累积损伤。

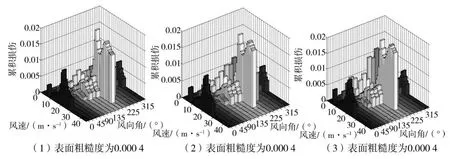
图11 每个工况下不同结构表面粗糙度对应的累积损伤

从图11中可以看出0～25°以及150～270°风向角工况造成的风致疲劳累积损伤较大。50～120°风向角以及280～300°风向角下的疲劳累积损伤较小,这和图10表示的结构位置处风速风向区间出现的概率一致。这说明,风向对结构的风致疲劳累积损伤影响较大,在出现概率大的风向区间内造成的风致疲劳累积损伤较大。

图11表明:在所有风向角下,风速为 25～30 m/s区间内的累计损伤较大;风速4.5 m/s,6.5 m/s时,结构发生涡激共振,此时的累积损伤也较大;大于38 m/s的风速产生的疲劳累积损伤为零,这是因为以结构风致疲劳寿命为重现期计算得到的每个风向区间下的最大风速都小于38 m/s;不同表面粗糙度结构在各个风速风向区间内疲劳累积损伤的趋势一致。

2.3 涡激共振对疲劳寿命的影响

该节分别用频域和时域的方法计算了不考虑以及考虑涡激共振影响的3种表面粗糙度下结构的风致疲劳寿命,其结果如表1所示。从表1中可知结构的涡激共振对结构风致疲劳寿命有一定程度的影响,是不可忽略的。图12给出了不同结构表面粗糙度下不考虑涡激共振时用频域方法计算的累计损伤随风速和风向的变化曲线。从(2)图中可以看出:当不考虑涡激共振影响时,小于10 m/s风速造成的疲劳累计损伤很小。

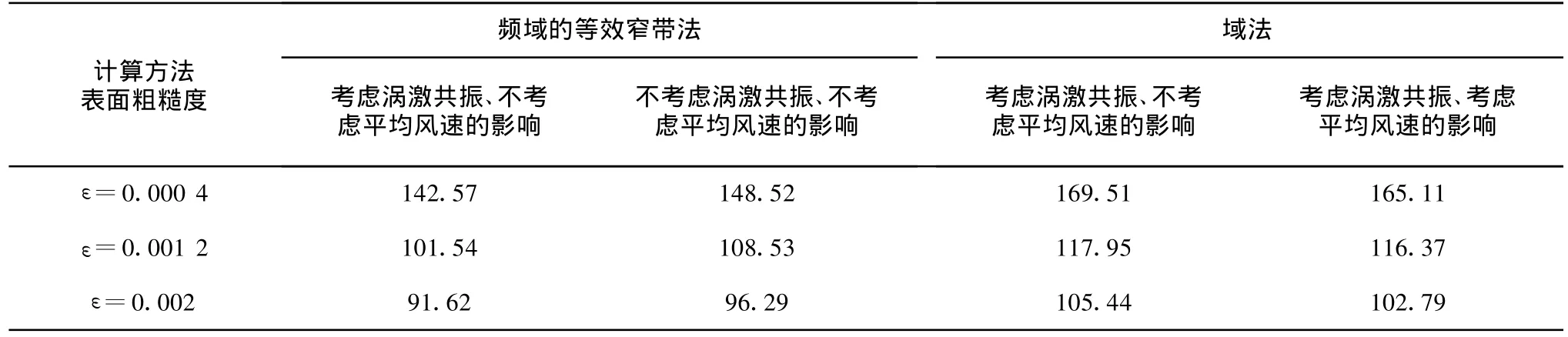
表1 考虑与不考虑涡激共振时得到的风致疲劳寿命的比较 a

图12 不考虑涡激共振时累计损伤随风速和风向的变化

3 结论

在求得结构不同风向、风速下风致响应以及结构所在位置处的风速风向联合分布函数的基础上,基于经典的疲劳累积损伤理论,对单体结构进行风致疲劳寿命估计。得到的几个重要结论为:风向对结构的风致疲劳累积损伤影响较大,在出现概率大的风向区间内造成的风致疲劳累积损伤较大,因此在进行风致疲劳寿命分析时,需根据气象资料得到建筑物位置处的风速风向联合分布函数;结构表面粗糙度对圆形柱状结构的风致疲劳寿命影响很大,结构的疲劳寿命随着表面粗糙度的增加而减小;涡激共振对结构的疲劳寿命有一定的影响,在计算圆形柱状结构的风致疲劳寿命时,不应该忽略涡激共振的影响;平均风荷载对结构的风致疲劳寿命影响较小。

[1]B N Pritchard.Steel chimney oscillations:a comparative study of their reported performence versus predictions using existing design techniques[J].Engineering Structres,1984,6(4):315-323.

[2]C VERWIEBE,A GLOCKNER.Failure of steel chimneys due to vortex excited vibration in the second mode[C]//Proceeding of 11th international conference on wind engineering.2003.Lubbok,Tex.

[3]邓洪洲,屠海明,王肇民.桅杆结构随机风振疲劳研究[J].土木工程学报,2003,36(4):19-23.DENG HONG-ZHOU,TU HAI-MING,WANG ZHAO-MIN.Study on stochastic fatigue of guyed masts under wind load[J].China Civil Engineering Journal,2003,36(4):19-23.

[4]张其林,U PEIL.欧美塔桅钢结构现状研究[J].特种结构,1996,13(2):58-63.ZHANG QI-LIN,U PEIL.Study about the current situation ofguyed maststructure in Europe and American[J].Special Structure,1996,13(2):58-63.

[5]P T RANVIK,G ALPSTEN.Dynamic behaviour under wind loading of a 90 m steel chimney[R].Alstom Power Sweden,2002.

[6]王世村,杨晓强.高耸结构风振疲劳的随机裂纹扩展分析[J].钢结构,2007.8(22):43-47.WANG SHI-CUN,YANG XIAO-QIANG.Stochastic analysis of fatigue crack growth for high-rise structures under wind loading[J].Steel Construction,2007,8(22):43-47.

[7]邓洪州,王肈民,马星.桅杆结构风振响应及疲劳研究进展[J].特种结构,2006,23(3):14-18.DENG HONG-ZHOU,WANG ZHAO-MIN,M A XING.State of the art paper about wind-induced response and fatigue of guyed masts[J].Special Structures,2006,23(3):14-18.

[8]GU M,XU Y L,CHEN L Z,et al.Fatigue life estimation of steel girder of yangpu cable-stayed bridge due to buffeting[J].Journal of Wind Engineering and Industrial Aerodynamics,1999,80:383-400.

[9]M CORAZAO,AG DAVENPORT.Asimple relationship between the gust response factorand fatigue damage[J].Journal of Wind Engineering and Industrial Aerodynamics,1988,30:45-54.

[10]M P REPETTO,G SOLARY.Dynamic alongwind fatigue of slender vertical structure[J].Engineering Structure,2001,23:1622-1633.

[11]M P REPETTO,G SOLARY.Dynamic crosswind fatigue of slender vertical structures[J].Wind and Structures,2002,5(6):527-542.

[12]M P REPETTO.Wind-induced response and fatigue of slender vertical structures[D].Genova The University of Genova,2003

[13]M PREPETTO,G SOLARY.Directional windinduced fatigue of slender vertical structure[J].Journal of Structural Engineering,2004,130(7):1032-1040.

[14]王钦华,顾明.钢天线风振疲劳研究[J].同济大学学报,2008.36(8):1040-1044.WANG QIN-HUA,GU MING.Directional windinduced fatigue of a real steel antenna[J].Journal of Tongji Unversity,2008,36(8):1040-1044.

[15]王钦华,顾明.钢质天线结构风振疲劳寿命估算方法比较研究[J].振动与冲击,2008,27(2):78-81.WANG QIN-HUA,GU M ING.Comparison between methods of structural fatigue life estimation[J].Journal of Vibration and Shock,2008,27(2):78-81.

[16]胡毓仁,陈伯真.船舶及海洋工程结构疲劳可靠性分析[M].北京:人民交通出版社,1996.

[17]王钦华,顾明.圆形线状结构风致响应的分析方法[J].振动工程学报,2010,23(2):151-157.WANG QIN-HUA,GU MING.Wind-induced response analysis for circular section structure[J].Journal of Vibration Engineering,2010,23(2):151-157.

[18]ESDU.Mean force,pressures and flow velocities for circular cylindrical structures:finite-length cylinders in uniform and shear flow[R].ESDU International.1981,London.