改进AHP-灰色关联分析的给水厂排泥水处理工艺优选模型

张 勤,华 佩,张 晋

(重庆大学 a.城市建设与环境工程学院;b.三峡库区生态环境教育部重点实验室,重庆400045)

给水厂在生产洁净水的同时,也产生了大量的生产废水,其主要来自沉淀池或澄清池排泥水及滤池反冲洗排泥水,水量约占水厂总净水量的3～7%[1]。在当前水环境污染日益恶化,水资源紧缺日益严重的情况下,有必要对排泥废水实施处理,并回收利用这部分水资源,从而减少水源污染、并在一定程度上缓解水资源紧缺的矛盾。因此,根据工程实际确定一个合理、高效的排泥水处理工艺流程就显得尤为重要。工艺流程的确定涉及到社会、经济、环境等诸因素的影响,即多因素决策问题。灰色关联分析是一种多因素统计分析方法,它是以各因素的样本数据为依据,用灰色关联度来描述因素间关系的强弱、大小和次序,已在社会、经济、农业等复杂系统多因素决策和工程技术综合评价中得到应用。然而,目前国内排泥水处理工艺的确定是以经济技术分析为主的单因素评价方法,缺乏多因素地、全面地评价体系,使得选定的待选方案难以实现全局最优。

针对上述排泥水处理工艺流程在甑选过程中存在的问题,运用灰色关联分析理论,以“重庆某电厂零排放项目”为工程背景,建立排泥水处理工艺优选模型。并引用最优传递矩阵对传统层次分析法进行改进,进而采用改进的层次分析法确定模型中各因素权重分配集合,实现改进层次分析与灰色关联分析法的结合,并以此模型对几种排泥水处理组合工艺流程进行系统地、定量地、全面地评价,确定适合该电厂净水站排泥水处理的最优工艺。

1 改进层次分析法

层次分析法(Analytic Hierarchy Process)[2-3],是一种应用于复杂系统综合评价中确定权重的重要方法。然而传统的层次分析法采用1～9比例标度法则构建判断矩阵,存在判断差异不明显,判断标度不易确定的问题,使得判断矩阵的不一致性极易发生。由此衍生出判断矩阵一致性检验、修正,以及修正不当所导致的权重集合分配的不稳定性、失真性等问题。

该文采用基于拟优传递矩阵的改进AHP,在构造判断矩阵时,采用3标度比例法则,并在构造判断矩阵的过程中引入最优传递矩阵[4-5],使得判断矩阵能自然满足一致性要求。省略传统层次分析法一致性检验及对传统判断矩阵的反复调整,克服了传统AHP的弊端。

1.1 建立递阶层次分析结构模型

给水厂排泥水工艺流程的设计优选是一个复杂的系统工程,它涉及社会、经济、环境等多个领域,而每个领域又受到多个子项因素的影响。为使整个系统条理化、层次化,将系统涉及的诸因素按照相互支配及隶属关系,构造层次结构模型。

首先,确定系统的目标层是排泥水处理工艺综合最优方案。其次,分析综合最优方案实现所涉及的各种经济,环境,管理因素,确定系统的准则层(指标层)。并按照各因素间互相支配或隶属关系分成若干子层。

1.2 构造判断矩阵

根据层次结构模型,运用成对比较法和3标度比例法则(见表1),构造各层对上1层每一因素的成对比较判断矩阵A:

表1 元素重要程度的比较值

1.3 建立最优传递矩阵

1.4 建立拟优传递矩阵

矩阵R为矩阵A的最优传递矩阵,则称矩阵D=eR是矩阵A的一个拟优化传递矩阵,且满足:。矩阵D为一致阵,自然满足一致性要求。通过拟优化传递矩阵D,可直接求得各因素的权重分配集合W,而无需进行一致性检验。

2 灰色关联分析数学模型

将灰色关联分析法引入到给水厂排泥水处理工艺优选中,通过分析判断待选方案与设定的理想方案的关联度的大小,来判断待选方案的优劣程度。

2.1 确定待选方案和理想方案

设初步设计的排泥水处理工艺待选方案为m个,每个方案包含n个评价指标,即:待选工艺方案为m个,每个方案包括n个指标：在对待选方案进行关联分析时,我们需要引入能够反映工艺流程优劣特征的理想方案,即:X通过待选方案与理想方案的关联度分析来判断待选方案的性能。

2.2 初始数据无量纲化处理

由于系统中各评价指标的物理意义不同,导致数据的量纲也不一定相同,不便于比较,或在比较时难以得到正确的结论。因此在进行灰色关联度分析时,一般都要进行无量纲化的数据处理。

对于成本型指标,令:

对于效益型指标,令:

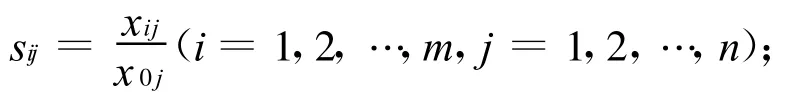
式中,xij为第i个待选方案的第j个指标的实际评价值,x0j为理想方案的第j个指标的评价值。

2.3 灰色关联系数的确定

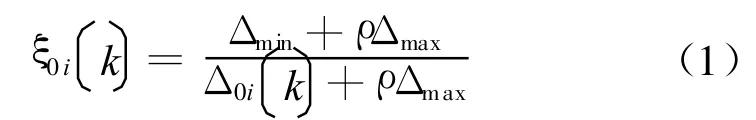
2.4 构建灰色关联系数矩阵

2.5 综合关联度的确定

待选方案与理想方案的关联度R可由下式计算:

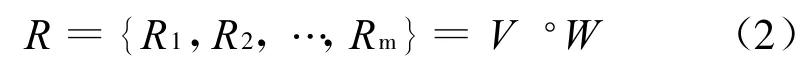
3 工程实例

重庆某电厂净水站,以渠江为水源,一期工程设计规模2万m3/d,供电厂生产及生活用水。净水站采取净水工艺如图1所示。

图1 净水站工艺流程图

目前该净水站排泥废水处理系统由于种种原因无法正常运转,致使澄清池排泥水及滤池反冲洗废水得不到有效处理而直接排入附近水体。为了有效减轻对周边环境及水体的污染,针对现有工艺存在的问题,以“重庆某电厂水系统零排放项目”为依托,经过设计研究,提出符合出水水质要求的几种排泥废水处理工艺流程,并对其进行综合评价,从而确定符合该净水站的最优工艺。

3.1 确定比较数列

考虑到原水水质较好,浊度很低,因此所选方案应能较好的改善污泥的浓缩及脱水性能。在传统“合流制”和“分流制”的基础上,充分考虑不同形式预处理对出水和污泥处理效果的影响。跟据国内外实验研究经验,经过设计分析,初步拟定以下几种方案[8-11],详见方案流程图2-5。

图2 x1方案流程图1

图3 x2方案流程图2

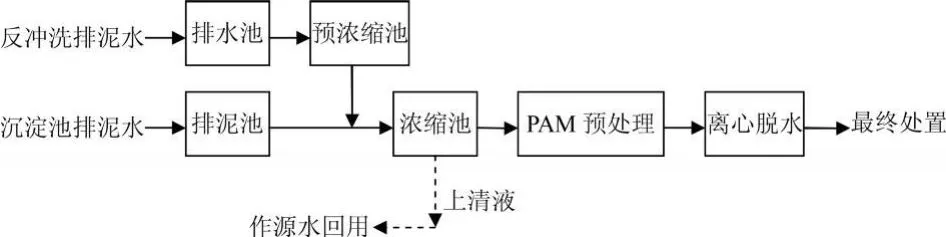
图4 x3方案流程图3

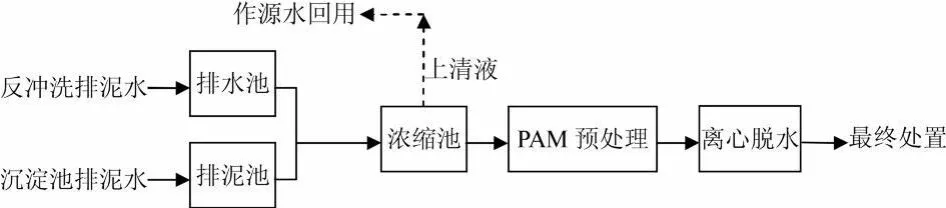
图5 x4方案流程图4

3.2 确定权重集合

3.2.1 建立递阶层次分析结构模型

选择较优的排泥水处理方案,既要考虑排泥水处理效果又要兼顾社会效益、经济效益、环境效益。经过对目标多样性的逐级解析,确定具有3个层次的结构模型,如图6所示。

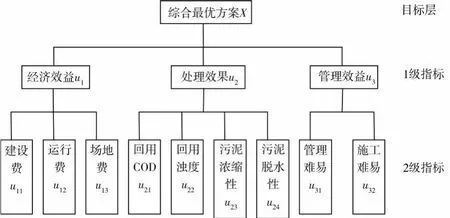
图6 层次的结构模型

3.2.2 构造判断矩阵

通过咨询相关专家意见[12-13],运用成对比较法和3标度比例法则,分别构造第1级指标、第2级指标对其相应上1层每一因素的成对比较阵,详见表2-5。

表 2 X-ui成对比较阵

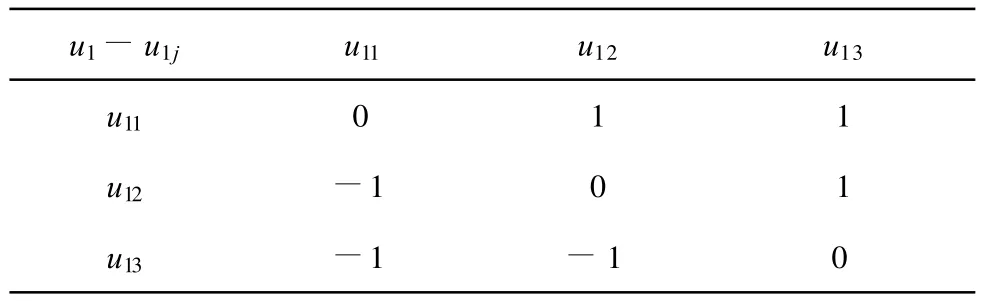
表3 u1-u1j成对比较阵

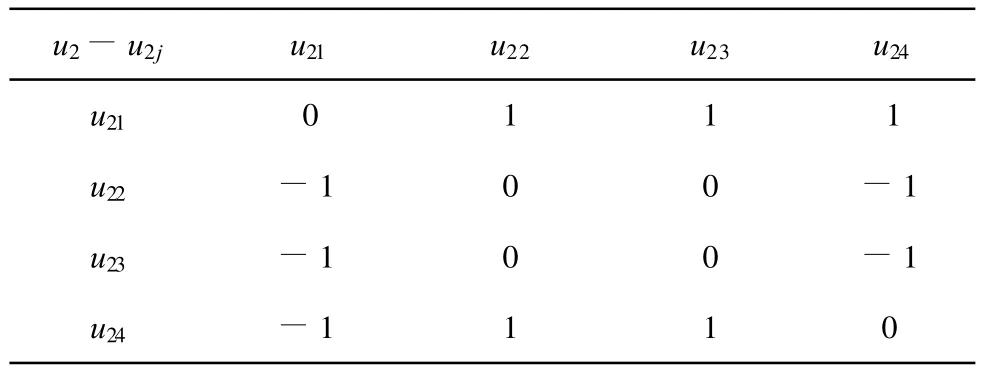
表4 u2-u2j成对比较阵

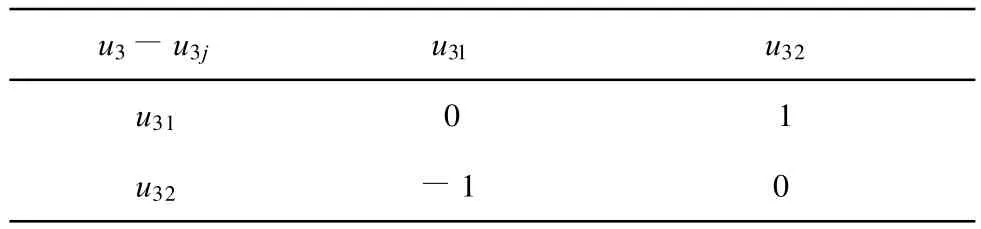
表5 u3-u3j成对比较阵

3.2.3 确定权重分配集合

以判断矩阵X-ui为例,建立判断矩阵X-ui的最优传递矩阵:

再建立矩阵R的拟优化传递矩阵D:

利用MATLAB仿真程序计算拟优化传递矩阵D的特征向量wi,即权重分配向量:

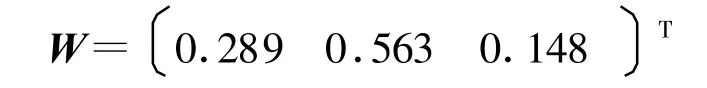
同理,依次计算各判断矩阵的权重并进行层次总排序,结果见表6。

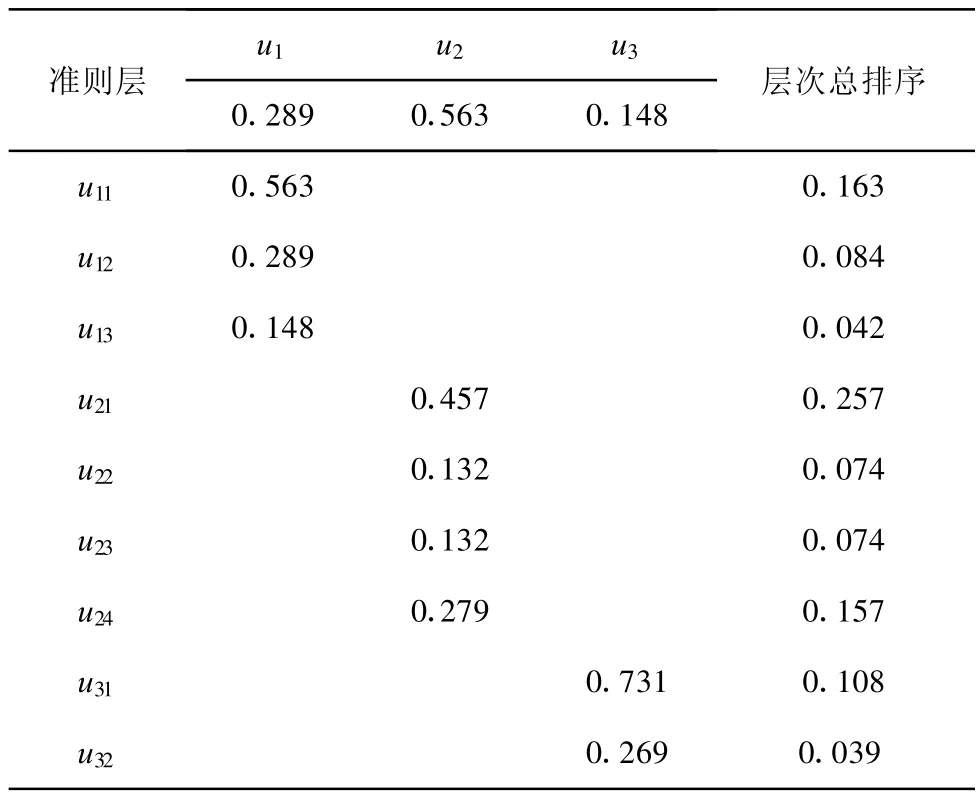
表6 层次总排序

3.3 构建灰色关联矩阵

以国内外给水厂排泥水处理工艺的试验研究及成功运行经验为基础,并结合专家的意见[14-15]。采用模糊数学5级划分法,构造待选方案与理想方案灰色关联排序矩阵,见表7。

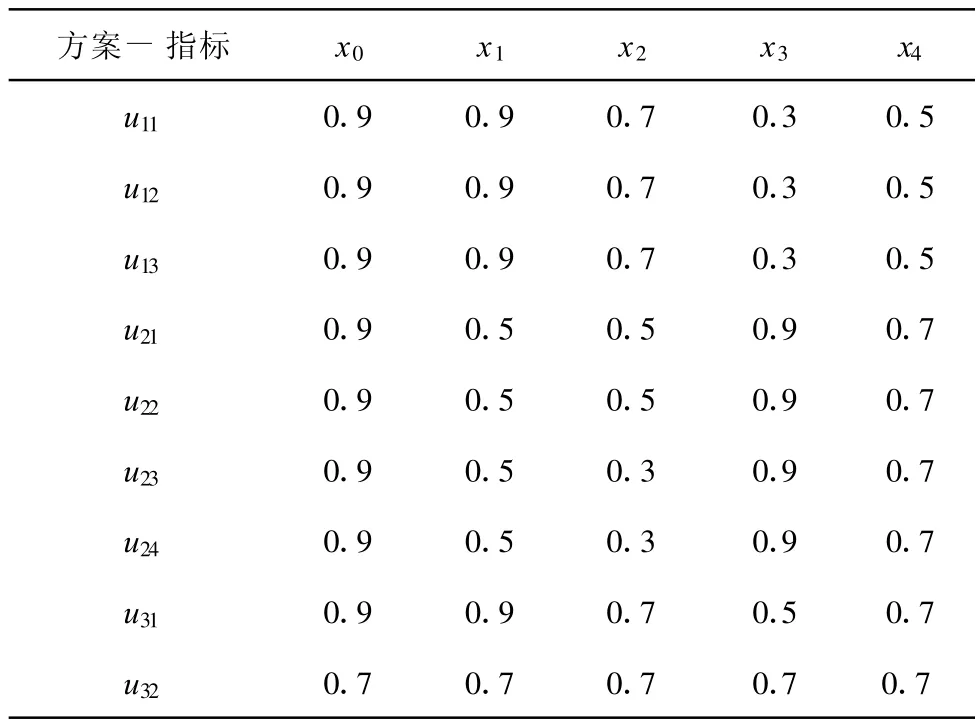
表7 灰色关联排序矩阵

对关联排序矩阵进行无量纲化处理,并根据式(1)得到灰色关联系数矩阵:

3.4 综合关联度的确定

通过对待选方案进行社会、经济、环境等因素的综合分析,由式(2)确定综合关联度:

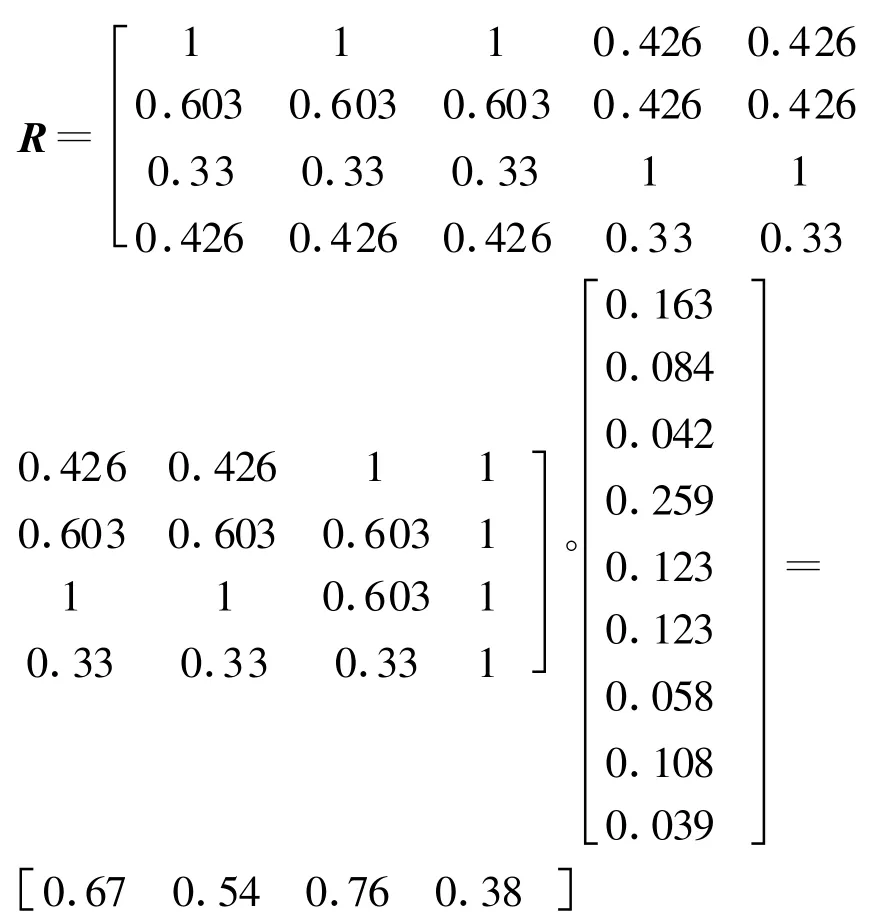
结果表明,按照关联度最大原则待选方案 x3综合评判为最优方案。由此,该水厂应采用工艺流程x3,如图7所示。

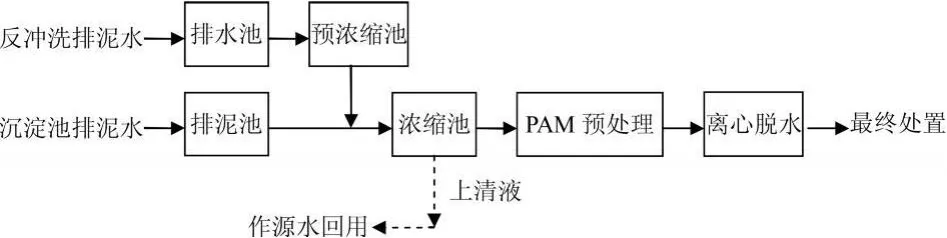
图7 最优方案

4 结论

1)应用模糊数学灰色关联分析理论和改进层次分析法,将对象视作系统,按照分解、比较、判断、综合的思维方式进行系统分析,建立了给水厂排泥水处理工艺优选模型。该模型计算简便、结果明确,便于决策者直接了解和掌握。

2)该文采用改进层次分析法确定评价因素的权重值,所需判断信息简单、直观、易为专家和决策者接受与掌握,所得的判断矩阵自然满足一致性要求,不需要进行一致性检验。

3)模型中整个运算过程,均可以利用MATLAB仿真程序得以实现。使得计算过程更加快捷,计算结果更加精确。

4)模型与现行的方案评价体系相比,克服了其存在的个别性、局限性等弊端,使选定的工艺流程较好的兼顾社会、经济、环境等诸因素的影响,为工程实践提供了全面的技术分析和定量的理论支持。

[1]向平,蒋绍阶.给水厂排泥水处理回用的若干问题[J].重庆建筑大学学报,2004,26(4):70-72.XIANG PING,JIANG SHAO-JIE.Some Issues about the Recycling Liquid Sludge Water from Water Treatment Plant[J].Journal of Chongqing Jianzhu University,2004,26(4):70-72.

[2]SAATY T L.There is no mathematical validity for using fuzzy number crunching in the analytic hierarchy process[J].Journal of Systems Science and Systems Engineering,2006,15(4):457-464.

[3]SAATY T L.Multi-criteriadecision making[M].RWS Publications,Pittsburgh,PA,1990.

[4]张卫中.改进的AHP及其在地灾易发程度分区中的实践[J].土木建筑与环境工程,2009,31(2):85-89.ZHANG WEI-ZHONG.Improved AHP Assessment Model and Its Practice in Geological Hazard Susceptibility Zoning[J].Journal of Civil,Architectural&Environmental Engineering,2009,31(2):85-89.

[5]白俊文,侍克斌.用改进的层次分析法(AHP)进行坝基防渗方案的优选[J].水利与建筑工程学报,2004,2(4):11-14.BAI JUN-WEN,SHI KE-BIN.Improved Hierarchy Analysis Process Used In Optimal Selection of Seepage Control Project of Dam Foundation[J].Journal of Water Resources and Architectural Engineering,2004,2(4):11-14.

[6]LU S H.Grey relational analysis coupled with principal component analysis for optimization design of the cutting parameters in high-speed end milling[J].Journal of Materials Processing Technology,2009,209(8):3808-3817.

[7]YANG F.Integrated Geographic Information Systems-Based Suitability Evaluation of Urban Land Expansion:A Combination of Analytic Hierarchy Process and Grey Relational Analysis[J].Environmental Engineering Science,2009,26(6):1025-1032.

[8]王正林.无锡市梅园水厂排泥水处理工程[J].中国给水排水,2005,21(3):70-73.WANG ZHENG-LIN.Sludge Water Treatment Project of Meiyuan Water Plant in Wuxi City[J].CHINA WATER&WASTE WATER,2005,21(3):70-73.

[9]陈士才,张磊.杭州市祥符水厂的排泥水处理工程[J].中国给水排水,2004,20(11):77-79.CHEN SHI-CAI,ZHANG LEI.Sludge water treatment project of meiyuan water plant in wuxi city[J].Ching Water&Waste Water,2004,20(11):77-79.

[10]Miyanoshita T.Economic evaluation of combined treatment for sludge from drinking water and sewage treatment plants in Japan[J].Journal of Water Supply and Technology-AQUA,2009,58(3):221-227.

[11]SMITH K M.Sewage sludge-based adsorbents:A review of their production,properties and use in water treatment applications[J].Water Research,2009,43(10):2569-2594.

[12]XU G R.Recycle of Alum recovered f rom water treatment sludge in chemically enhanced primary treatment[J].Journal of Hazardous Materials,2009,116(2/3):663-669.

[13]闫嘉钰.基于灰色综合关联度的数控机床热误差测点优化新方法及应用[J].四川大学学报:工程科学版,2008,40(2):160-164.YAN JIA-YU.Application of a New Optimizing Method for the Measuring Points of CNC Machine Thermal Error Based on Grey Synthetic Degree of Association[J].Journal of Sichuan University(Engineering Science Edition),2008,40(2):160-164.

[14]TONY M A.Conditioning of aluminium-based water treatment sludge with Fenton's reagent:Effectiveness and optimising study to improve dewaterability[J].CHEMOSPHERE,2008,72(4):673-677.

[15]穆瑞,张家泰.基于灰色关联分析的层次综合评价[J].系统工程理论与实践,2008,10:125-130.MU RUI,ZHANG JIA-TAI.Research of hierarchy synthetic evaluation based on grey relational analysis[J].Systems Engineering-Theory&Practice,2008,10:125-130.