边坡锚固工程分析中的水平条分法

魏作安,朱 彬,万 玲,周永昆,陈宇龙

(1.重庆大学a.西南资源开发及环境灾害控制工程教育部重点实验室;b.资源与环境科学学院,重庆400044;2.湖南科技大学湖南省煤矿安全开采技术重点实验室,湖南 湘潭411201)

极限平衡法是通用的一种用于边坡稳定性分析的计算方法[1-5]。中国相关资料和规范要求采用极限平衡法中的垂直条分传递系数法进行边坡加固的受力分析[6-7]。然而垂直条分传递系数法在分析锚杆和锚索加固边坡时,垂直划分的条块会与加固结构体锚杆等存在交叉,同时,锚杆提供的加固力的作用点在坡面上,而资料和规范中提出的锚杆的作用力的作用点是滑面处,这些与实际情况存在偏差,使得该方法在应用中存在一些缺陷,势必影响边坡加固工程的效果。为此,在相关资料提出的用于加筋土坡稳定性计算的水平条分法基础上[8-10],将水平条分法进行了拓展,使其能更好地适应用锚杆和锚索等边坡加固措施的分析与计算。

1 垂直条分传递系数法的缺陷分析

在边坡稳定性计算分析中,通过分析地质资料或边坡稳定计算,确定边坡潜在的最危险滑面位置(如图1(a))。然后按照设计规范对边坡进行加固初步设计,布置锚杆或锚索等加固工程(如图1(b))。最后采用垂直条分传递系数法对锚杆锚索等加固工程的参数进行计算(如图1(c))。

从图1(c)中可以看出,如果为了提高分析的精度,可将条块划分较细,这样一根锚杆或锚索会与多个条块相交,即出现加固体与条块相交叉的现象。一旦出现交叉,那么如何将这根锚杆的作用力分配到多个条块上就非常困难,从而影响到计算结果的可靠性与准确性。

图1 边坡锚固分析示意图

采用垂直条分传递系数法的条块受力分析如图2所示,图中,Ei-1为第i-1块滑体下滑力,Ei为第i块滑体下滑力,Wi为第i块滑体重量,αi为第i块滑体滑面的倾角,Ti为锚杆作用在第i块滑体的加固力,β为锚杆与水平面的夹角,Ni为滑面上正应力,Si为滑面的抗滑力。

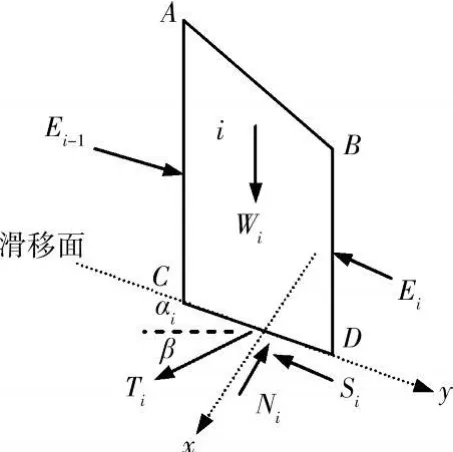
图2 条块受力分析简图

从受力分析图中可以看出,假定锚杆或锚索的作用力Ti是在滑面上(图2中CD边)[11]。从锚杆作用原理可以知道(如图3),锚杆是通过位于滑床稳定岩土层中的锚固段EF和坡面锚头O产生锚固力的。从力的3要素(大小,方向和作用点)可以知道,锚杆作用在滑体上的锚固力 Ti的作用点是坡面(AB边)上O点处,而非滑移面处。而且许多研究成果亦表明锚固力的传递深度远不能到达滑移面处[12]。所以,将锚固力移至滑移面处会使计算结果与实际情况产生偏差,亦会给边坡加固工程造成不利影响。

图3 锚杆作用力分析简图

2 边坡锚固工程中的水平条分法

2.1 水平条分法原理

水平条分法(HSM)最早是由Lo和 Xu[8]于1992年提出来的。后来Shhgholi等人[9]对该方法进行了发展与改进,并将该方法应用于加筋土挡土墙地震作用下的稳定性分析。Nour等人[10]对该方法进行了详细推导与完善。水平条分法主要是应用于加筋土挡土墙的稳定性分析与计算,水平条分法(HSM)的条块受力分析如图4。图中,Vi、Vi+1分别为第i-1和i+1条块作用在第i条块的垂直作用力(相当上覆土层的重量),为第i-1和i+1条块作用在第i条块上的水平剪切力为第i块滑体重量,αi为第i块滑体滑面的倾角,为加筋材料提供给第i块的加固力,N i为滑面上正应力,Si为滑面的抗滑力,kv、kh分别为水平和垂直方向的地震力作用系数。

图4 水平条分法及条块受力分析简图

根据极限平衡原理,每个条块上的水平方向和垂直方向上的作用力平衡,即,

如果是圆弧型滑面,则条块的力矩亦要平衡,即有,

通过建立受力平衡方程(式(1)和(2))与力矩(式(3)),则可以求解出地震作用下需加筋材料提供的加固力 T′i。

如图5,边坡锚固工程作用在条块上的力Ti与加筋材料的作用力T′i不同,前者与水平方向有个夹角β。为此,将Ti分解成水平方向和垂直方向的2个分力,即

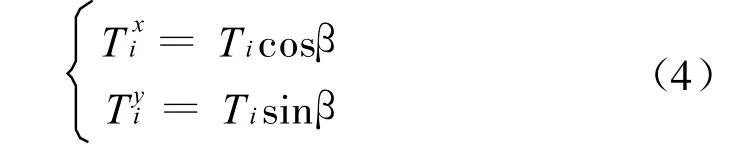
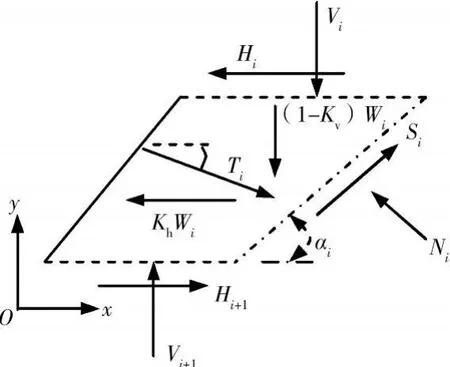
图5 锚杆加固边坡水平条分法条块受力分析简图

将式(4)代入式(1)和(2)中,垂直方向的力按每个条块考虑平衡,水平方向的力则按整个滑体考虑平衡,这样可以消除条块间的水平剪切力,可以得到滑体在x与y方向上的受力平衡方程,即为:

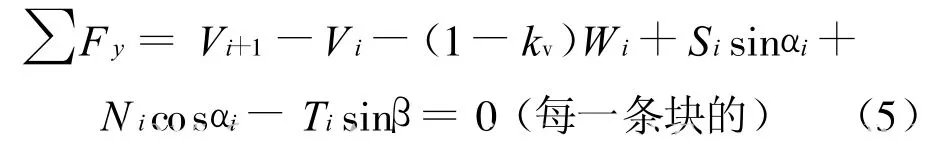
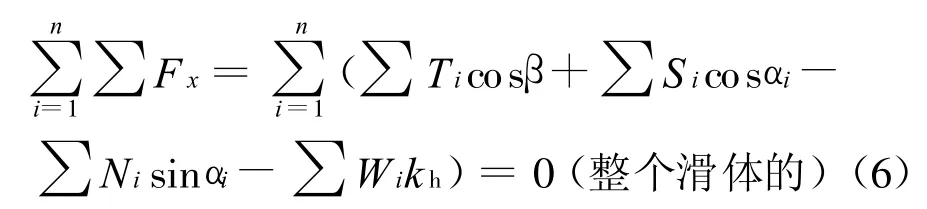
因此,按照常规的传递系数法计算步骤,由坡顶往坡脚逐个条块进行计算,这样可以求出各条块上的锚杆加固力Ti等参数值。如果滑面为圆弧型,则同样可以考虑力矩平衡。

2.2 水平条分法在边坡锚固工程中的应用

伊朗北方高速公路公司计划在德黑兰(Tehran)到查路斯(Chalus)之间修建一条高速公路,以改善2个城市之间的交通条件。高速公路在K13+200处有一个人工开挖、高度为50.0 m的土质边坡(如图6)。由于边坡比较高,而且又是土质边坡,同时设计的边坡又陡(伊朗公路设计公司设计的坡度为3:2),边坡开挖到第3级台阶时发生了局部垮塌(图7),所以,必须对该边坡进行加固处理。

图6 设计的边坡以及部分开挖后的情况

图7 边坡上的局部垮塌

在综合计算分析后,结合中国经验,设计采用框架梁+锚杆为主的加固方案(如图8),其中锚杆的长度为12.0 m,间距为 2.0 m,采用 Φ32、S400钢筋(伊朗当地钢材)。在锚杆受力分析中,按照水平条分法进行了计算。为了与垂直条分法进行比较,采用余推力法进行了加固计算,2种方法的计算模型如图9,条块的初始数据见表1。按照倾角20°施加16.83 k N/m2的锚杆作用力后,水平条分法计算得到的边坡稳定系数为1.30,而垂直条分法计算得到的边坡稳定系数为1.21。说明边坡达到相同的稳定系数,采用水平条分法计算施加的作用力比垂直条分法要小,要经济。

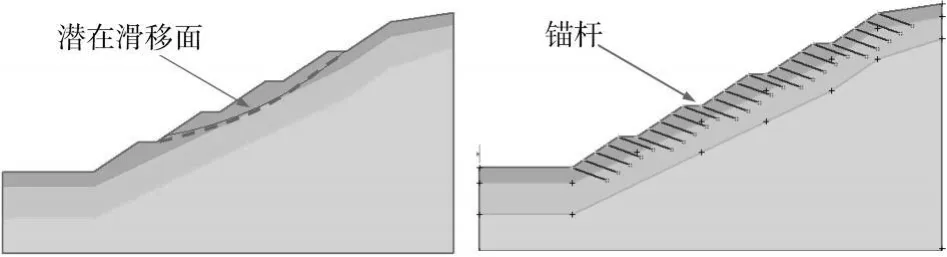
图8 稳定计算与加固方案

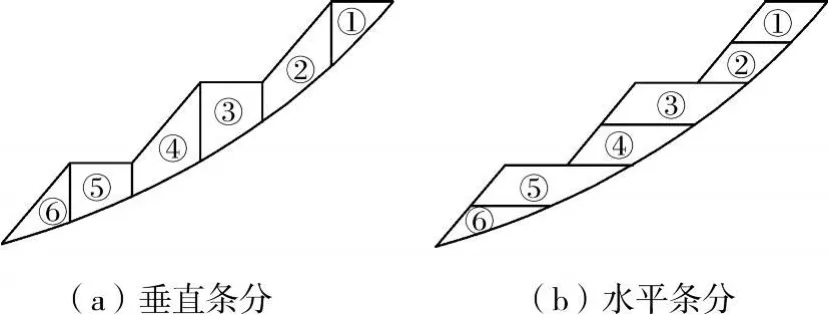
图9 两种条分法条块划分示意图

表1 2种条分法各条块初始数据

3 结论

1)经过分析,垂直条分传递系数法在边坡锚固分析中存在一些缺陷,其中包括条块与锚固体之间发生交叉,分析时锚固力作用点的位置与实际情况不同,使计算结果与实际情况会产生出入,影响边坡锚固工程的质量与效果。

2)将加筋土坡稳定性计算的水平条分法进行拓展,把倾斜的锚固力分解为垂直和水平2部分,这样就可以将该方法移植到边坡锚固工程的计算分析中,克服了垂直条分法的缺陷,受力分析与实际情况更吻合。

[1]DASBRAJA M.Principle of Geotechnical Engineering[M].5th ed.California:Thomson Learning,2005.

[2]OZTEKIN B,TOPAL T,KOLAT C.Assessment of degradation and stability of a cut slope in limestone,Ankara-Turkey[J].Engineering Geology,2006,84(1):12-30.

[3]WEI ZUOAN,LI SHIHAI,Wang J G,et al.A dynamic comprehensive method for landslides control[J].Engineering Geology,2006,84:1-11.

[4]华东水利学院土力学教研室.土工原理与计算:上、下册[M].北京:水利电力出版社,1984.

[5]WEI ZUOAN,YIN GUANGZHI,WAN LING,et al.Case history of controlling a landslide at Panluo openpit mine in China[J].Environmental Geology,2008,54(4):599-709

[6]中国地质环境监测院.长江三峡工程库区滑坡防治工程设计与施工技术规程[M].北京:地质出版社,2001.

[7]GB 50330-2002建筑边坡工程技术规范[S].北京:中国建筑工业出版社,2002.

[8]LO SC R,XU D W.A strain based design method for the collapse limit state of reinforced soil walls and slopes[J].Canadian Geotechnical Journal,1992,29(8):832-842.

[9]SHAHGHOLI M,FAKHER A,JONES C J F P.Horizontal slice method of analysis[J].Geotechnique,2001,51(10):881-885.

[10]NOURI H,FAKHER A,JONES C J F P.Development of horizontal slice method for seismic stability analysis of reinforced slopes and walls[J].Geotextiles and Geomembranes,2006,24(2):175-187.

[11]李春盛.喷锚网支护法在边坡加固中的应用[J].路基工程,1999(4):53-55.LI CHUN-SHENG.Application of shotcrete,rock bolting and wire mesh for slope reinforcement[J].Road Foundation Engineering,1999(4):53-55.

[12]孙学毅.边坡加固机理探讨[J].岩石力学与工程学报,2004,23(16):2818-2823.SUN XUE-YI.Study on mechanism of slope reinforcement[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(16):2818-2823.