钢管塔架K型加肋节点的承载力分析

刘红军,李正良

(重庆大学 土木工程学院重庆,400045)

K型加肋节点构造是输电塔架、塔式起重机肢体等类似钢结构的重要环节。目前国内外对钢管相贯焊节点的研究比较充分,1981年 Yura等人对1979年前的数据进行了分析整理,用经验法建立了改进的管节点极限承载力方程[1]。1996年Kang C T、Moffat D G和Mistry J对空间TT型节点在主管受压状态下的承载力性能进行了试验和理论分析的研究工作[2]。1999年,Soh C K和Chan T K等在屈服线理论的基础上,对受轴向荷载的X型节点的承载力计算建立了2种理论模型[3]。中国《钢结构设计规范》(GB 50017-2003)对此类节点的承载力给出了特定承载力性能进行了试验和理论分析的研究工作[2]。1999年,Soh C K和Chan T K等在屈服线理论的基础上,对受轴向荷载的X型节点的承载力计算建立了2种理论模型[3]。中国《钢结构设计规范》(GB 50017-2003)对此类节点的承载力给出了特定的计算方法,其适用范围为相贯焊K型节点,将其运用到螺栓连接的钢管-板连接的K型节点是否可行尚缺乏可靠的依据。最近几年由于中国大力推广钢管塔的应用,因此也有很多学者开始了此类节点受力性能研究。吴龙升,孙伟民等[4]基于4个U型插板钢管连接节点,考虑材料非线性和几何非线性对U型插板的钢管节点承载力特性进行了非线性有限元分析,得出空间焊缝极限屈服承载力要比一般平面焊缝屈服极限承载力低,用一般平面焊缝的计算公式计算不合适。陈金凤,金晓华,傅俊涛等[5-6]通过试验和有限元分析对平面K型十字插板进行了研究,考察了十字插板连接节点的受力特点,并指出了主管管壁与节点板连接处存在较为明显的应力集中现象。傅俊涛在其博士论文中通过几个钢管插板节点试验及有限元分析研究了K型插板节点的受力性能、塑性扩展过程,揭示了此类节点的破坏机理和2种典型破坏形式,获得其极限承载力及其随节点几何参数的变化规律,得到了一些基本结论。

国际上由于一些发达国家交流特高压输电线路的建设,钢管塔应用较早,对钢管塔试验研究进行得较早。日本早在20世纪80年代就在钢管塔节点构造方面作了较深入的研究工作,并形成了节点设计的一整套方法[7]。目前,中国电力行业规范中没有此类节点的设计验算方法,在设计钢管塔时较多地借鉴了日本的方法。但由于钢材型号、性能、设计体系方面与中国有较大的差别,完全照搬日本的做法是不科学的。Soh[8-10],余世策等[11-15]采用屈服线模型对钢管节点的极限承载力进行了简化理论分析,其计算结果与试验结果较为吻合。文献[14]通过钢管塔带连接板的K型节点进行足尺模型试验,采用圆环-母线梁分离模型,根据钢管能量理论和虚功原理,推导出了三管轴力作用下此类节点的极限承载力公式,但没有考虑加强肋对承载力的影响。对有加强环,加强肋的钢管节点中国没有相应的设计验算方法。该文通过试验、有限元以及理论分析对钢管输电塔架环型加肋节点的承载力进行了研究,为工程设计提供了理论依据。

1 试验研究

1.1 试验样本

图1 K型插板连接构造图

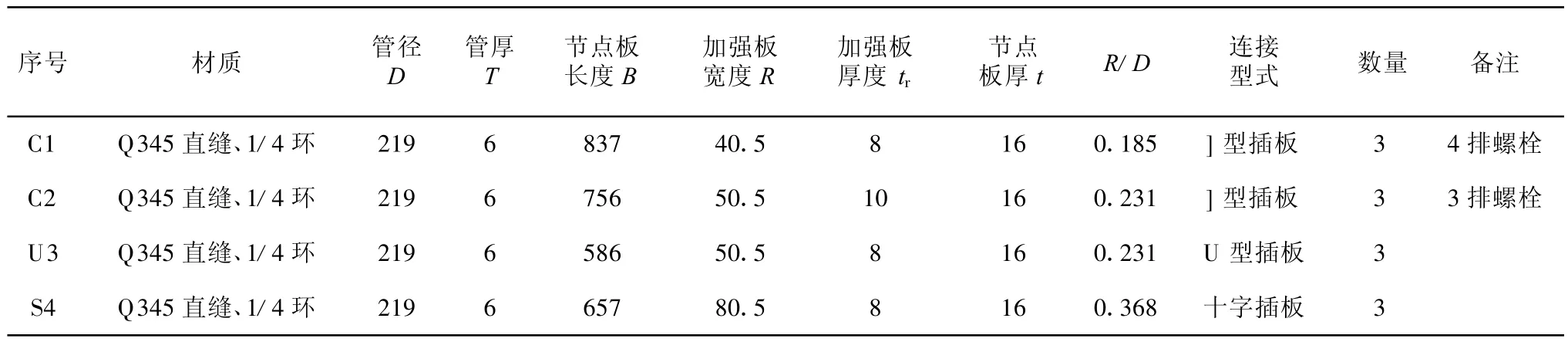
表1 试验样本

图2 K型节点承载力试验装置图

图3 承载力确定示意图

试验加载为单向分级加载,为详细描述节点板应力的变化情况,试验加载方案考虑很小的加载增量,每级加载后停顿1 min后继续加载,直到试件破坏无法再加载为止,详细加载方案见表2。

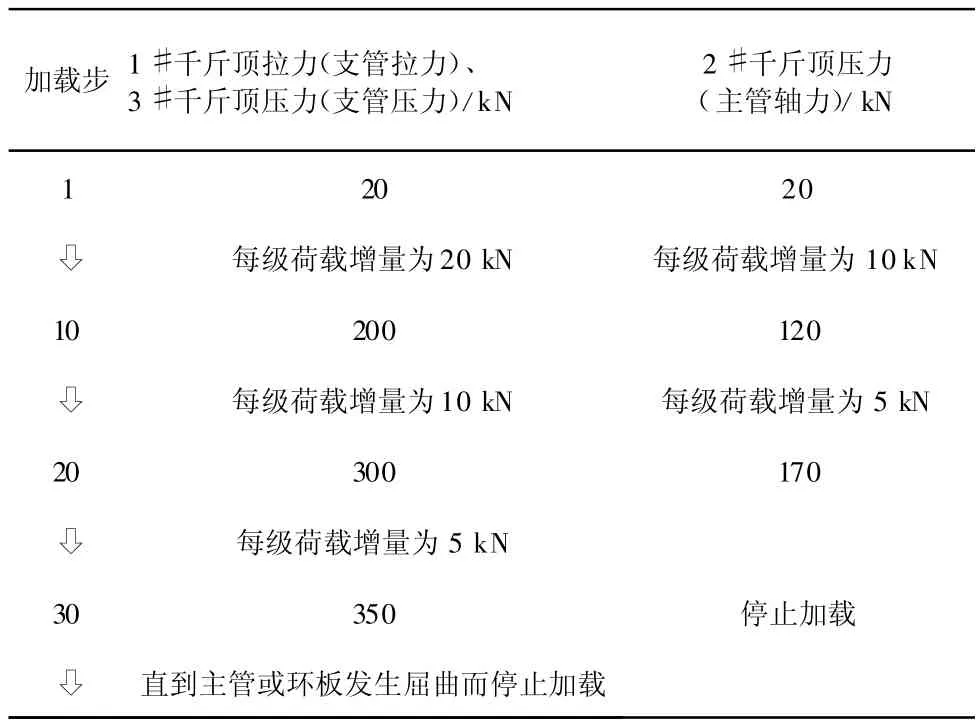
表2 节点承载力试验加载方案

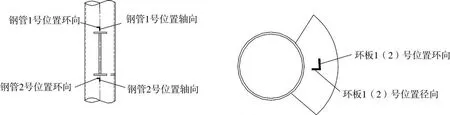
图4 关键点应变布置图

1.2 试验结果

试验观察得出试件破坏模式为局部破坏,钢管与节点板交界处发生局部屈曲,其破坏模式有以下现象:1)构件S4的主管在钢管1号位置处管壁产生局部凹陷,其变形量较大;在2号位置处管壁产生局部隆起,其变形量较小,2)构件U3和C2的钢管1号位置处的破坏形式与钢管2号位置处的破坏形式正好相反,管壁产生局部凹陷,其变形量较小,环板有明显变形,其变形量较钢管小;3)构件C1的钢管1号位置处局部屈服程度较钢管2号位置处明显,但无环板1号位置的变形量明显。因此将着重分析钢管1,2号位置附近管壁以及环板1(2)号位置的局部屈曲情况,并以此建立极限承载力估算公式。其关键点的荷载—应变曲线和荷载—位移曲线见图5。

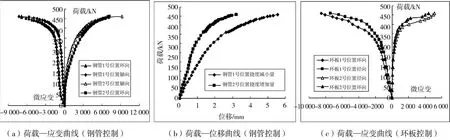
图5 加强节点荷载—变形曲线

从图5可以看出:随着荷载的增加,测点的应变由线性变化呈现非线性变化,表明测点附近已经进入了屈服阶段。当荷载继续增加,测点均进入塑性,钢管节点迅速发生破坏,即钢管和加强环板附近塑性域已经贯通,最终变为机构体系,节点达到极限承载状态。

2 有限元分析

从实验结果可以看出,节点的破坏模式分主管破坏和加强环板破坏2种方式,即:节点的承载力分为主管控制和加强环板控制。为了进一步清楚加肋钢管节点区域的应力分布情况,采用ANSYS的壳单元shell181来模拟节点板,加肋环板和钢管,不考虑焊缝的影响。有限元计算模型如图6所示。

图6 有限元模型

为了验证有限元结果的有效性,取构件S4的试验结果与其有限元结果进行比较,见图7,钢材本构关系与材性试验得到的结果一致。泊松比取0.3,弹性模量为198 k N/mm2,名义屈服强度σP0.2=418 MPa,抗拉强度 σb=520 MPa,延伸率 δ=18%。

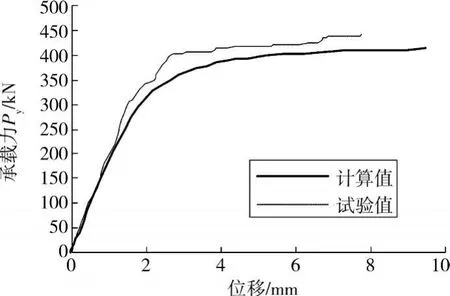
图7 节点承载力与位移关系曲线比较

图8 加肋节点等效受力图

2.1 参数分析

为了进一步清楚加肋钢管节点区域的应力分布情况,K型节点的受力状态可以等效为图8所示,且借助有限元分析了管壁,环板宽度和厚度以及不同加肋情况等主要参数对承载力的影响,影响曲线见图9所示。

图9 节点不同参数对承载力的影响曲线

2.2 建议公式

对有限元的结果进行拟合得到其建议公式:

1)1/4加强板

P y为 P1,P2,P 3的最小值。

2)1/2加强板

Py为 P1,P2,P3的最小值。

3)全圆环加强板

①K ≤1.0时,

Py为P1,P2的最小值。

fy为钢管的屈服强度;fr为加强环板屈服强度。

3 理论分析

假设材料为理想弹塑性材料,不考虑剪力对弯矩塑性铰的影响,只考虑受压端的局部变形。根据试验结果和有限元分析,全加强环板节点破坏机理假设为四铰破坏机理,1/4(1/2)加强环板节点破坏机理假设为五铰破坏机理,变形前后塑性铰的发展如图10所示。图10(a)中塑性铰1,3和4,6是固定的,铰2和5是自由的且由荷载P y确定其位置;图10(b)中塑性铰1,3和5是固定的,铰2和 4是自由的且由荷载Py确定其位置;环型补板近似于钢管有效幅度b 1的部分组成的T形面的环,根据式(11)确定环形补板的有效幅度,即b 1。当b 1确定后,T形截面的塑性中性轴的位置能确定,因此能得到塑性中性轴与圆心的距离,即D P/2。将D P代入(1)～(10)得到此类节点的估算极限承载力。

根据虚功原理:

MP为截面塑性弯矩。

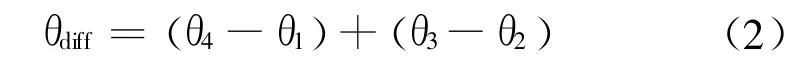
1)1/4(1/2)环型加肋节点

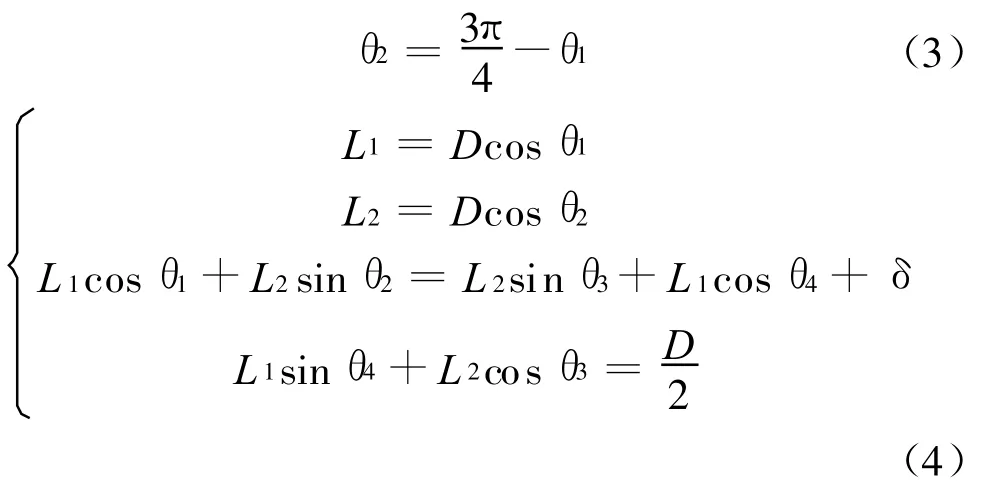
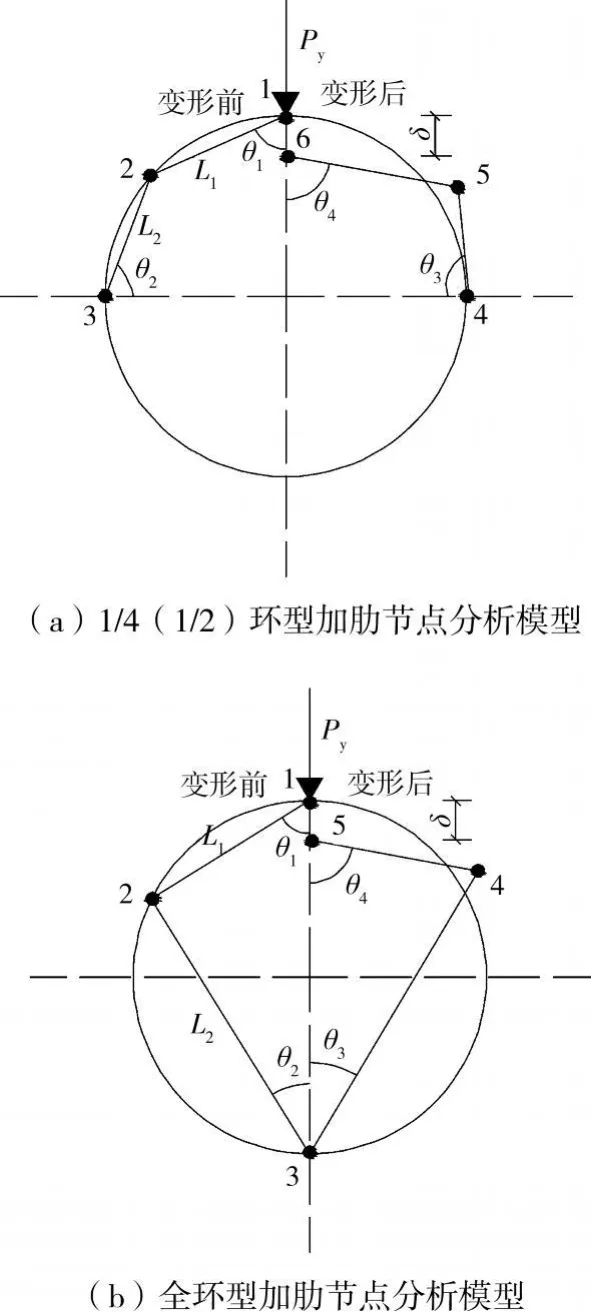
图10 加肋节点分析模型

得到:

2)环型加肋节点(单侧)

根据几何关系:

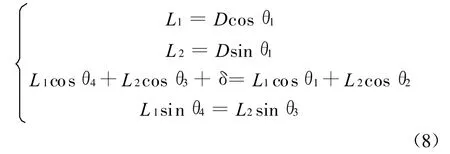
得到:

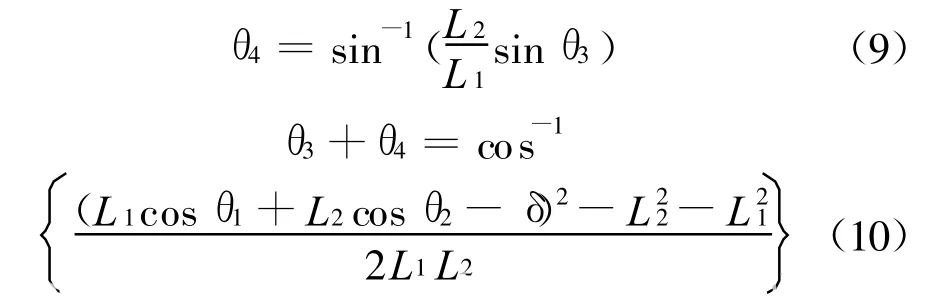
环型补板近似于钢管有效幅度b1的部分组成的T形面的环,见图11-图12。此时环型补板的有效幅度由采用B Thurlimann所提出的算式确定:

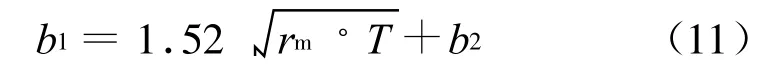
图11 环形补板的有效幅度

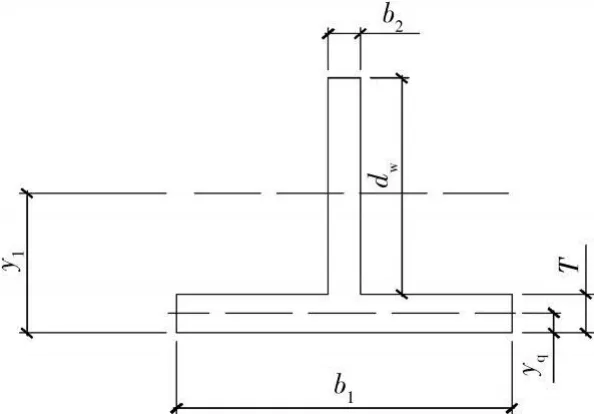
图12 T形截面图

根据截面塑性区的中性轴高度:

得到截面塑性系数为:

式中:A为T形截面面积。

则截面塑性弯矩为:

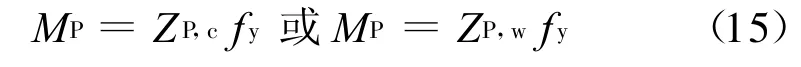
表3 不同计算方法得到加肋节点承载力的的比较

从表3可以看出:日本《送电钢管铁塔制作基准》得到的承载力是偏保守的,对于K型节点,此公式不能准确的预估节点的极限承载力。极限分析模型能较好的预估此类节点的极限承载力。建议公式具有一定的适用性。

4 结论

根据上述研究,可以得出如下结论:

1)在节点板和支管自身承载力满足要求的前提下,加肋K型插板连接节点的破坏模式主要是主管,加肋板和节点板相交的区域。在此区域主管发生局部屈曲或环板发生屈曲。环板发生屈曲又分为弯矩引起和剪力引起2种情况来讨论。

2)根据试验和有限元结果建立的极限分析模型是合理有效的,这个模型把由环板控制和主管控制2种破坏模式通过T型截面的塑性中性轴的高度来考虑,同时考虑了环板与钢管的共同作用。但模型没有考虑剪力和拉力对节点承载力的影响,故模型计算结果偏小。

3)通过K型节点不同参数对承载力影响的研究可以看出,1/4加肋节点与1/2加肋节点的受力性能类似,设置在节点板两侧的加肋构造和加肋方式能有效提高节点的极限承载力。所提出的建议公式较全面的考虑了节点的破坏模式和影响参数对承载力的贡献,具有一定的适用性,能为工程设计提供理论依据。

[1]YURA J A,EDWARDS I F,ZETTLEMOYER N.Ultimate capacity of circular tubular joints[J].J.Struct.Div.,ASCE,1981,107(10):1965-1984.

[2]KANG C T,MOFFAT D G,MINISTRY J.Strength of DT tubular joints with brace and chord compression.J.Struct.Engrg[J].ASCE,1998,124(7):775-783.

[3]SOH C K,CHAN T K,YU S K.Limit analysis of ultimate strength of tubular X-joints[J].J.Struct.Engrg.,ASCE,2000,126(7):790-797.

[4]吴龙升,孙伟民,张大长.U型插板钢管连接节点承载力特性的非线性有限元分析[J].南京工业大学学报:自然科学版,2008,30(1):92-96.WU LONG-SHENG,SUN WEI-NIN,ZHANG DACHANG.Nonlinear FEM analysis of bearing behavior of steel tube connection with U-type f lash board[J].Journal of Nanjing University of Technolog:Nature Science Editor,2008,30(1):92-96.

[5]傅俊涛.大跨越钢管塔节点强度理论与试验研究[D].上海:同济大学,2006.

[6]陈金凤.空间异型钢管相贯节点的理论与试验研究[D].武汉:华中科技大学,2005.

[7]输电线路钢管塔制作基准[M].日本铁塔协会,1985.

[8]CHI KING LEE,LIE SENG TJHEN,CHIEW SING PING,et al.Numerical models verification of cracked tubular T,Y and K-joints under combined loads[J].Engineering Fracture Mechanics,2005,72:2006.

[9]ELCHALAKANI M,ZHAO X L,GRZEBIETA R H.Plastic mechanism analysis of circular tubes under pure bending[J].International Journal of Mechanical Sciences,Elsevier,2006,44(6):1117-1143.

[10]ZEINOD-DINI M,HARDING J E,PARKE G A R.Contribution of ring resistance in the behavior of steel tubes subjected to a lateral impact[J].International Journal of Mechanical Sciences,Elsevier,2004,42(12):2303-2320.

[11]郭健,孙炳楠.钢管塔中管-板连接节点的破坏全过程分析[J].工业建筑,2006,36(12):83-86.GUO JIAN,SUN BING-NAN.The whole course analysis of failure behavior of tube-gusset joint in steel tubular tower[J].Industrial Construction,2006,36(12):83-86.

[12]余世策,孙炳楠,叶尹.高耸钢管结点极限承载力的试验研究与理论分析[J].工程力学,2004,21(3):155-161.YU SHI-CE,SUN BING-NAN,YE YIN.Experimental study and theoretical analysis of ultimate strength for steel tubular joint of tall towers[J].Engineering Mechanics,2004,221(3):155-161.

[13]王小丽,翁雁麟,关富玲.X型圆管相贯结点极限承载力分析[J].市政技术,2006,24(1):34-36.WANG XIAO-LI,WENG YAN-LIN,GUAN FULING.Ultimate strength of the circular tubular X-joints[J].Municipal Engineering Technology,2006,24(1):34-36.

[14]鲍侃袁,沈国辉,孙炳楠,等.高耸钢管塔K型结点极限承载力的试验研究与理论分析[J].工程力学,2008,25(12):114-122.BAO KAN-YUAN,SHEN GUO-HUI,SUN BINGNAN,et al.Experimental study and theoretical analysls of ultimate strength for steel tubular K-joint of tall towers[J].Engineering Mechanics,2008,25(12):114-122.

[15]金晓华,傅俊涛,邓洪洲.输电塔十字插板连接节点强度分析[J].钢结构,2006,21(5):41-44.JIN XIAO-HUA,FU JUN-TAO,DENG HONGZHOU.Intensity analysis for cross-gusset connection steel tubular joints of transmission towers[J].Steel Construction,2006,21(5):41-44.