电子对抗装备器材保障仿真决策模型研究*

李 宁 刘 洪

(电子工程学院 合肥 230037)

1 引言

高技术局部战争条件下,电子对抗装备已成为夺取制电磁权的主战装备,对战争的进程和结局有着深远的影响。现代战争的非线性、高消耗和高需求,使得电子对抗装备器材(以下简称器材)保障的作用更加突出。然而,在复杂多变的战场环境中,快速有效地完成器材保障任务是一个涉及众多因素的复杂问题,由于器材保障活动本身的动态性和诸多因素的不确定性,仅靠人工的判断和处理已不能达到快速有效的目标和不适应模拟仿真的要求。有必要将器材保障活动结构化,建立器材保障模型,为电子对抗装备器材保障的仿真打下基础。

维修保障资源的有限性是仿真模型的核心,主要涉及维修保障资源的供应及调度的建模,包括对各种维修保障资源的分类、定量、配置和优化。器材保障决策系统总体框图如图1所示。

总控模块是整个系统的核心,负责系统的协调运行、控制、系统管理和系统维护等功能。

图1 器材保障决策系统总体框图

器材补给决策负责为系统提供器材补给的策略。它根据战场各维修单位的现有器材数量和各单位下一战斗时节所担负的维修任务等情况,为器材保障指挥员提供器材补给的辅助决策信息,便于指挥员进行器材补给的宏观决策。

器材保障方案生成[1]负责为系统生成器材补给方案,它是在器材补给决策系统做出器材补给决策之后开始工作的。按照战时器材补充及时、准确、适量的要求,制定器材保障计划,决定器材从哪个仓库补给,需要补充的数量,所用运输工具,所走路线等。

保障力量部署负责对器材保障部(分)队在数量、时间、地点上进行配置,其目的是使器材保障力量形成一个完成的有机整体,确保稳定安全,使保障能力充分发挥出来,完成保障任务,提高保障效率。

本文以电子对抗作战中的器材保障工作为背景,仅就器材补给决策进行研究。

2 器材消耗预计算法[2]

2.1 战场器材消耗分析

现在战争条件下,电子对抗装备极易遭受到电子武器的软杀伤和火力打击,造成战斗损伤;同时,由于正常使用消耗和严酷使用消耗,装备还面临着非战斗损伤。

2.2 基本假定

1)战斗损伤与非战斗损伤是彼此独立的;

2)各种战斗损伤事件之间是相互独立的;

3)目标区域中共有Q台相同装备,每个单元在每台装备中只有一个;

4)不考虑硬火力毁伤和电磁毁伤同时损坏一个单元的情况。

2.3 模型的建立

1)硬火力损伤器材消耗量Nai的确定

根据硬火力造成的战斗损伤的特点,一个损伤事件可能包含一个或多个单元的损伤。损伤事件与损伤单元间的关系可用表1描述。

表1 损伤事件与单元的关系

装备的硬火力损伤概率为A(n),记为P,则单元i的消耗量为:

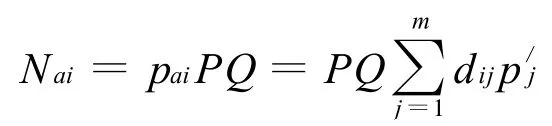
2)电磁毁伤器材消耗量Nbi的确定

设电磁毁伤事件发生的概率为pj,电子对抗装备的毁伤概率为pm,结合 Nai的确定方法,可以类似推出Nbi的消耗量为:

3)非战斗损伤器材消耗量Nci的确定

非战斗损伤器材消耗量为正常使用消耗加上严酷使用消耗。严酷使用消耗可由正常消耗量乘以比例系数k得出。正常使用消耗量在装备研制和平时使用过程中已有经验值,设为N0i,则有:Nci=(1+k)N0i

4)器材需求量计算

消耗的器材量即为所需的器材量,综上所述,第i类器材需求总量为:Ni=Nai+Nbi+Nci

3 器材补给决策模型

针对维修分队所需器材的状况,通过器材补给辅助决策系统,决定是否对维修分队进行器材补给。

3.1 基于存储论确定战时器材补充时机和补充量[3～4]

战时,维修分队必须携带一定量的维修器材,随着维修工作的进行,器材消耗到一定程度必须进行补充。决策模型的基本假定:

1)器材消耗。为了简化问题,我们假设器材的消耗是连续均匀的,消耗速度为R。

2)器材补充。器材的补充是将在仓库中的器材运送给维修分队,这个过程需要一段时间,称为拖后时间。所以为了保障战斗的顺利进行,在进行器材补充时,必须将拖后时间考虑进去,提前进行补充。这里假设器材供给量充足,不会缺货。

3)战时器材保障的损失。它包括两方面因素:一指在战场上进行器材补给的过程中,受到敌人袭击、破坏,造成的器材损失;二指器材存放在库所中,会造成一定器材损失,以及维修分队携带定量器材,造成机动性降低而造成的损失。

假定模型的消耗是连续的、稳定的[5],消耗速度R为常数;设每隔t时间补充一次器材,则这段时间内弹药消耗量为Rt,设补充途中损失的弹药费用为c2。

器材存放在库所中,由于自然条件或受到敌人的袭击会造成一定的损失,设器材存放在库所中损失系数为C1,则t时间内平均损失的弹药用所需平均费用表示为:。则t时间内总的平均费用为

由此得出,弹药的最佳补充时间间隔是t0,每次的弹药补充量为Q0。

3.2 战时器材保障策略的选择[6]

战时器材保障策略决定何时补充及补充数量。s表示库所器材消耗的最低限度,S表示库所器材的最高储备标准。常见的策略有三种:

t0循环策略,每间隔时间t0,补充器材Q。

(s,S)策略,每当库所存储量 x＞s时不补充,当 x≤s时补充,补充量Q=S-x。

(t,s,S)混合策略,每经过时间t0检查存储量x,当 x＞s时不补充,当 x≤s时补充,补充量Q=S-x。

若在战时采取的是以(s,S)策略为主的器材保障策略。确定s时,要将保障部队接到命令后,从出发到抵达阵地这一段时间考虑进去,还要考虑我方的保障能力、敌人的封锁、自然条件等情况。

4 结语

信息化战场的激烈对抗对其电子对抗装备器材保障工作提出了更高的要求,作者将器材保障决策模型应用于教研室的“电子对抗装备器材保障仿真系统”,取得了良好的效果,增强了器材保障的有效性、针对性,为电子对抗装备保障的发展做出了一点有益的探索。

[1]许国银,陈森发.基于现代物流技术的精确保障及我军构建策略[J].物流技术,2005(9)

[2]俞康伦,于洪敏.基于FUZZY控制的弹药供应辅助决策[J].军械工程学院学报,2000(12)

[3]张最良.军事运筹学[M].北京:军事科学出版社,1997

[4]王兴录.战时勤务学[M].北京:兵器工业出版社,2003

[5]赵新泽.线性规划的新方法和应用[M].北京:世界图书出版公司,1997

[6]王进发,李励.军事供应链管理[M].北京:国防大学出版社,2004