某舰载伺服系统位置控制器设计与仿真研究*

祁海禄 樊小平 詹盛武

(中国船舶重工集团公司第710研究所 宜昌 443003)

1 引言

伺服控制系统的任务首先要保证系统输出量的变化能够紧紧跟随其输入量的变化,并要求具有一定的跟随精度[1]。因此,良好的响应快速性、较小的超调量和稳态误差成为衡量伺服控制系统性能最基本的指标要求。当系统要求的控制性能很高时,单独采用开环控制或闭环控制难以达到系统的要求,可采用开环控制和闭环控制相结合的复合控制方法,用以提高系统的控制精度[1]。在复合控制系统中,带有负反馈的闭环控制起主要调节作用,带有前馈的开环控制则起辅助的补偿作用。

某舰载伺服系统要求能够实现系统的快速定位和跟踪,传统PID控制难以达到理想的控制效果,模糊自整定PID控制能够实现系统的快速、高精度定位,但跟踪效果仍难以达到系统的要求。前馈控制可用来提高系统的跟踪性能[2]。为了实现某舰载伺服系统的快速、高精度定位和跟踪,本文基于该系统的仿真模型,对系统位置控制器设计了模糊自整定PID+输入前馈控制复合控制算法,并与传统PID控制、模糊自整定PID控制、传统PID+输入前馈控制复合控制算法进行了仿真比较分析;仿真结果表明,模糊自整定PID+前馈控制复合控制算法的控制效果更优,较小角度阶跃输入响应的调节时间比传统PID控制短0.2s以上,稳态、跟踪误差较其它方法最小。

2 某舰载伺服系统组成及其仿真模型

2.1 伺服系统组成

图1 某舰载伺服系统结构框图

某舰载伺服系统的结构如图1所示。该伺服控制系统的交流伺服电机是一种永磁无刷直流电机(BLDCM);交流伺服驱动器是与无刷直流电机相配套的高精度、宽范围调速系统,其控制电路主要由速度环和电流环组成;位置检测环节采用高精度的旋转变压器作为测角元件。

2.2 伺服系统仿真模型

某舰载伺服系统模型的建立,依据永磁无刷直流电机(BLDCM)的数学模型[3]、交流伺服驱动器的控制电路模型、机电传动系统动力学等理论基础建立系统速度环模型,如图2所示;在速度环模型的基础上加上位置控制器即构成位置伺服系统的总体仿真模型,如图3所示。

图2 某舰载伺服系统速度环仿真模型

图3 某舰载伺服系统总体仿真模型

图3所示的系统总体仿真模型中,速度环模块为图2所示的仿真模型的封装结果。

3 复合控制算法理论基础

3.1 PID控制

在实际应用中,90%以上的控制工程中至今仍然采用PID及其改进形式的控制器[4],主要是因为PID控制具有算法简单、鲁棒性好、可靠性高等优点。PID控制本质上是一种线性控制,由给定值r(t)与实际输出值y(t)构成偏差:

将偏差的比例、积分和微分通过线性组合构成控制量,对被控对象进行控制。其控制规律为:

式中 ,kp、ki、kd分别为比例、积分、微分系数。

传统PID控制最主要的问题是参数一经整定,在整个控制过程中都是固定不变的,难以达到更加理想的控制效果。因此,研究简单有效的变参数PID控制算法应用于伺服系统中显得十分必要。将先进控制策略和传统PID控制相结合是解决上述问题的一条有效途径。

3.2 模糊自整定PID控制

模糊控制是以模糊集合论、模糊语言变量及模糊逻辑推理为基础的智能控制,可以引入人的判断技巧和推理能力,对于非线性、复杂对象的控制显示了鲁棒性好、控制性能高的优点。为了改进传统PID控制的不足,可将模糊控制和传统PID控制相结合,发挥二者的优势,实现PID参数在线模糊自整定,即模糊自整定PID控制。

模糊自整定PID控制运用模糊数学的基本理论和方法,把规则的条件、操作用模糊集表示,并把这些模糊控制规则及有关信息作为知识库存入到计算机知识库中,计算机根据控制系统的实际响应情况,运用模糊推理,自动实现对PID参数的调整。这种控制器具有传统PID控制器的线性形式和非常数的控制参数,可看作是对传统PID的一种扩展,把人的判断推理经验用模糊规则表示出来,对PID参数进行在线实时自调整,打破了传统PID的局限性。其原理框图如图4所示。

图4 模糊自整定PID控制原理框图

在图4中,模糊控制器的输入变量可根据需要选择一维形式(一个输入变量误差e)或二维形式(误差e和误差变化率ec两个输入变量),输出变量可根据需要选择个数及其形式(如 kp、ki、kd或Δ kp、Δ ki、Δ kd)。模糊自整定 PID 控制器根据模糊逻辑原理和不同时刻的输入检测值,利用模糊推理规则在线对PID参数进行修改,以满足不同的输入量对控制参数自整定的要求,从而使被控对象具有良好的动、静态性能。

3.3 前馈控制

前馈控制实质上是一种开环控制,在自动控制系统中起辅助的补偿作用,一般不单独使用,通常与反馈控制一起使用,构成前馈-反馈复合控制系统。其基本控制思想是[2],当闭环系统为连续系统时,使前馈环节与闭环系统的传递函数之积为1,从而实现输出完全复现输入,可用来有效提高系统的跟踪性能。前馈控制的基本原理结构框图如图5所示。

图5 前馈控制基本原理结构框图

由图5有:

为使跟踪误差恒为零,则有:

只要满足式(4)的条件,即Gf(s)和Gp(s)互为逆函数,就有:E(s)=0,系统的输出量完全无误差地复现输入量。然而,实际过程的传递函数都是在一定条件下简化而来的,或由于工作环境的变化等而导致参数漂移,没有办法获得精确的过程逆模型,因此无法达到理论上的设计要求。针对实际问题,通常采用微分前馈以实现在一定程度上提高系统的跟踪精度[5]。

4 位置控制器设计

4.1 模糊自整定PID控制器设计

4.1.1 确定模糊控制器的维数

有关维数选取是模糊PID控制器结构设计中最为基本的内容,从工程整定方面的简单性考虑,“一维输入—三维输出”形式的模糊PID最为优越;从鲁棒性性能指标考虑,二维模糊PD(或滑模)控制器是最佳选择[6]。本文根据仿真曲线及算法改进结果,同时兼顾考虑工程整定参数的简单性,模糊控制器的维数选择为一维,即一维输入(误差e)—二维输出(比例系数kp、积分系数ki)。

4.1.2 模糊语言变量值及其隶属度函数的确定

确定了模糊控制器的维数,模糊语言变量也已确定,即为误差e、比例系数 kp、积分系数 ki。从工程整定的简单性考虑,为减少模糊规则数,本文对输入、输出语言变量的语言值均选择 Z(零)、S(小)、M(中)、B(大),即将误差e取绝对值后模糊化作为模糊控制器的输入变量。由于三角形隶属度函数表示方便、计算简单,因此各语言变量值的隶属度函数均采用三角形隶属度函数。

4.1.3 模糊控制规则的建立

根据模糊PID参数自整定原则[7]及工程技术人员的经验,制定出的模糊控制规则如表1所示。模糊决策采用Mamdani推理方法,解模糊采用面积重心法。

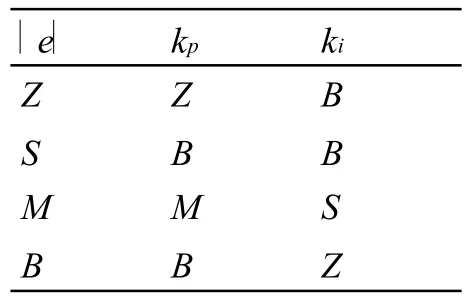
表1 模糊自整定PID控制推理规则表

4.2 位置控制器总体设计

由图5可看出,前馈设计实际上是基于复合控制思想,即复合控制算法的设计对象为Gp(s)和Gf(s),使得控制器的输出变为u(s)=Gp(s)+Gf(s)。根据前馈控制原理,复合控制算法中的Gf(s)设计为给定信号的微分前馈控制项,Gp(s)设计为传统PID控制或模糊自整定PID控制。Gp(s)和Gf(s)的设计顺序为先 Gp(s)后Gf(s),设计Gp(s)时,给定信号为阶跃输入;设计Gf(s)时,Gp(s)参数已确定,并不再改动,给定信号为正弦输入,然后确定Gf(s)参数。按照上述思路设计位置控制器,其总体结构如图3所示。

5 系统仿真与分析

基于Matlab/Simulink仿真环境,根据图3建立伺服控制系统的总体仿真模型,并加入不同的输入信号,对加入了位置控制器的伺服控制系统进行仿真与分析。

5.1 系统阶跃响应仿真与分析

由于输入前馈控制项为给定信号的微分,对于阶跃输入信号来说,微分前馈控制项恒为0。因此,是否加入前馈控制项不影响系统的响应结果。图6只给出了传统PID控制、模糊自整定PID控制的阶跃响应仿真曲线(限于篇幅,此处只给出了输入幅值分别为30°和1°的阶跃响应曲线)。

图6 系统阶跃响应仿真曲线

表2列出了部分不同阶跃输入响应的性能指标数据,其中σ表示相对给定值的绝对超调量,t0.1(s)表示输出响应到达并停留在0.1°误差带内所需的最小时间,es s表示稳态误差。

表2 系统阶跃响应性能指标仿真数据

由图6和表2可看出,模糊自整定PID控制和传统PID控制相比,当阶跃输入幅值在30°以上时,前者稳态误差较小;当阶跃输入幅值在30°以下时,前者调节时间更短、稳态误差较小。

5.2 系统正弦跟踪仿真与分析

图7分别给出了未加前馈控制项时传统PID控制、模糊子自整定PID控制,加入了前馈控制项时传统PID控制、模糊自整定PID控制的正弦跟踪误差曲线。其中,正弦输入信号的周期为5s,幅值为5°。

图7 正弦输入信号位置跟踪误差曲线

由图7可以看出,模糊PID控制与传统PID控制相比,前者正弦跟踪效果较好;加入前馈控制项后,正弦输入信号位置跟踪效果显著改善。四种控制方法相比,模糊自整定PID+前馈控制复合控制算法控制效果更优。

5.3 系统等速跟踪仿真与分析

图8分别给出了未加前馈控制项时传统PID控制、模糊自整定PID控制,加入了前馈控制项时传统PID控制、模糊自整定PID控制的等速跟踪误差曲线。其中,等速跟踪的给定信号为5°/s。

由图8可以看出,模糊PID控制与传统 PID控制相比,前者等速跟踪效果较好;加入前馈控制项后,斜坡输入信号等速跟踪效果明显改善。四种控制方法相比,模糊自整定PID+前馈控制复合控制算法控制效果更优。

图8 斜坡输入信号等速跟踪误差曲线

6 结语

模糊控制器是基于专家的经验并通过语言规则的形式实现了系统输入与输出之间的非线性映射关系,从而实现了参数的非线性增益调整[6];加入输入信号前馈控制项,改善了系统的跟踪性能。本文研究的模糊自整定PID+前馈控制复合控制算法,仿真结果表明控制效果较优,能够实现系统快速、高精度定位和跟踪的控制要求,是实现伺服系统位置控制的一种有效方法。

[1]戴忠达.自动控制理论基础[M].北京:清华大学出版社,1991

[2]刘金琨.先进PID控制 MATLAB仿真[M].北京:电子工业出版社,2004

[3]纪志成,沈艳霞,姜建国.基于 Matlab无刷直流电机系统仿真建模的新方法[J].系统仿真学报,2003,15(12):1745～1749

[4]王蕾,宋文忠.PID控制[J].自动化仪表,2004,25(4):1～6

[5]曾玉金.高性能交流伺服系统及其复合控制策略研究[D].杭州:浙江大学,2004

[6]胡包钢,应浩.模糊PID控制技术研究发展回顾及其面临的若干重要问题[J].自动化学报,2001,27(4):567～584

[7]常满波,胡鹏飞.基于MATLAB的模糊PID控制器设计与仿真研究[J].机车电传动,2002(5):34～36