一种单站纯方位跟踪中的非线性最小二乘方法*
2010-08-11穆晓斌
穆晓斌
(海军驻北京作战系统军事代表室 北京 100036)
1 引言
由于潜艇隐蔽攻击的需要,纯方位跟踪问题(BOT)引起了广大学者的普遍关注。到目前为止,对该问题的研究已经建立了大量、丰富的方法。文献[1]对纯方位目标跟踪系统的可观测性进行了分析,得出了系统可观测的必要条件。文献[2]介绍了确定性参数计算方法和基于最小二乘原理的方位平差法。文献[3]建立了直角坐标系下的推广卡尔曼滤波算法,这种滤波器常常导致发散。文献[4]采用了拟线性滤波器,即在直角坐标下将非线性量测方程拟线性化,而拟线性滤波器的解出现了偏倚。文献[5]在改进的极坐标系下选择目标运动参量,再利用这种参量建立推广卡尔曼滤波器,但这种滤波器计算量太大。文献[6]构建基于修正极坐标系下的近似线性最小二乘滤波算法,并以它作为卡尔曼滤波器的初始化算法。但是这些方法仍然满足不了潜艇日益增长的隐蔽攻击需要。最小二乘滤波具有不计误差统计特性,使用简单,实现容易、有效的特点。因而得到了最为广泛的使用,成为潜艇火控子系统中一种不可缺少的滤波方法。目前各种论文和杂志上论述的采用线性最小二乘滤波的方法较多,而对于基于非线性最小二乘滤波方法的叙述和讨论较少。因此对于新方法和新思路进行研究和讨论对于纯方位跟踪问题的深入研究具有重要意义。
2 纯方位法问题的描述
纯方位跟踪问题,是指观测器利用观测器材量测到的一组受污染的目标方位,来估计目标的运动参数。

图1 目标-观察者运动态势图
具体采用数学和物理模型的描述如下:见图1目标和观察者的运动态势。以地理正北方向为y轴,地理正东方向建立直角坐标系。O点为观察者(本艇)观测到第1个目标方位βm(1)时的本艇位置,(xo(i),yo(i))为ti时刻观察者的位置坐标。(βm(1),βm(2),…,βm(i))为本艇观测到的目标方位序列。假定目标做匀速直线运动,在已知βm(1)时 ,利用(D1,Cm,Vm),就可以唯一地确定目标的运动轨迹;在已知(xt0,yt0,vtx,vty)时,也可唯一确定目标的运动轨迹。(D1,Cm,Vm)分别代表目标的初距、航向和航速。(xt0,yt0,vtx,vty)为目标初始位置横纵坐标、横向速度分量和纵向速度分量。
所谓的纯方位跟踪,就是利用方位观测序列(βm(1),βm(2),…,βm(i))及(xo(i),yo(i)),ti等已知量,在假定目标做等速直线运动的情况下,求解(D1,Cm,Vm)或(xt0,yt0,vtx,vty)的过程。
3 模型建立及求解
这里选择x=[x1 x2 x3 x4]T=[xt0 yt0 vtx vty]T作为待估计的变量。设 T为采样周期,初始时刻为设置为零,第iT时刻测量的目标方位记为βm(i)。以观测者的初始位置为坐标原点,正北方向为坐标纵轴,正东方向为坐标横轴建立直角坐标系。
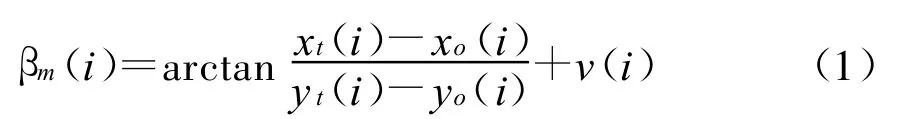
由式(1)得
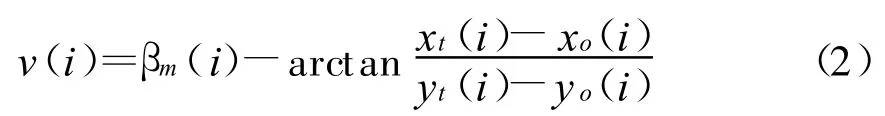
对式(2)两边取正切得
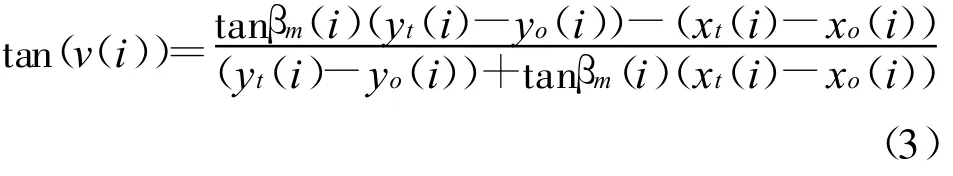
将 xt(i)=xt0+iTvtx和yt(i)=yt0+iTvty代入式(3)得
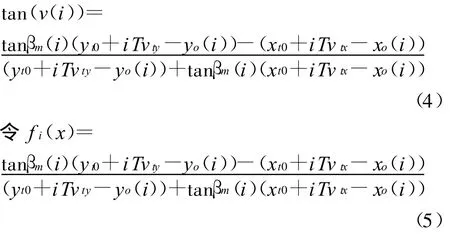
设计目标函数为

这样对x的估计转化为求F(x)的极小化问题minF(x)。由于fi(x)是x的非线性函数,F(x)的极小化是一个非线性最小二乘问题。文献[6]给出了解非线性最小二乘问题的两种迭代方法,本文选择了Marquardt方法,这种方法把一个正定对角矩阵加到Ak)-1上去,改变原矩阵的特征值结构,使其变成条件数较好的对称正定矩阵,并且不需要作一维搜索。这里给出针对单站纯方位跟踪问题算法描述,描述的方法采用伪码。伪码中 A、f的计算公式,参见式(7)、式(8);式(8)中偏导数的计算公式,参见式(9);x*为算法的估计值。
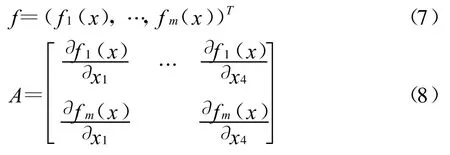


图2 Marquardt方法的伪码描述
4 仿真分析
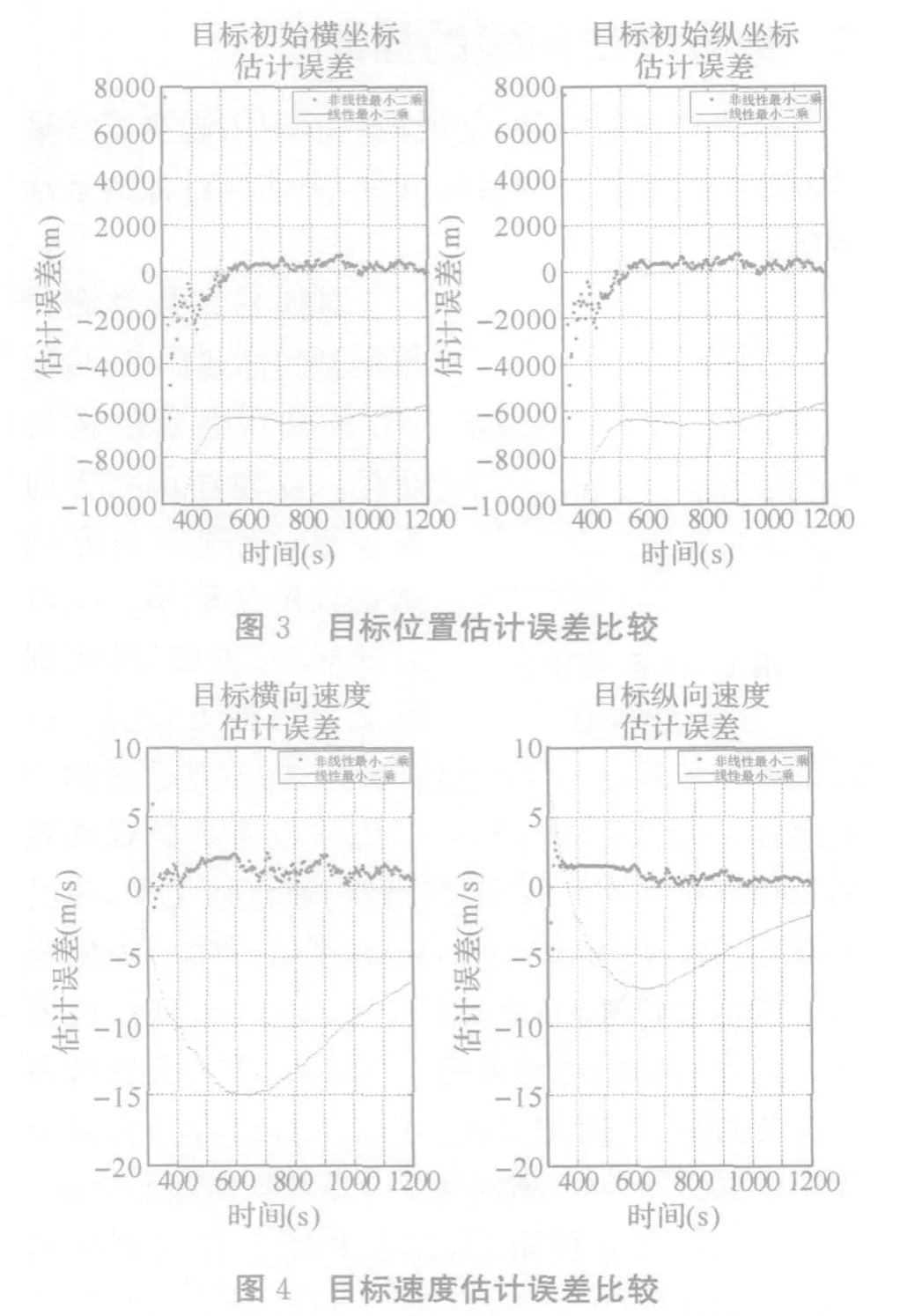
为了考察这种非线性最小二乘方法的计算效果,特进行了仿真分析。仿真时间为20min,目标初始距离为20km,初始方位为45°,航速为 8m/s,航向为120°;观测者初始位置为(0,0),先走方位航向5min,再走方位航向加90度15min,航行速度为4m/s。测量方位角采用真实方位角值附加均方差为0.3°的高斯白噪声生成。由于观测者机动,纯方位跟踪问题才有解,解算从观测者机动以后开始。取初始点 x=(9000,9000,5,-3),初始参数∂1=0.01,增长因子β=10,允许误差ε=1.0e-010。仿真将非线性最小二乘方法的解算结果跟线性四维最小二乘方法[7]的解算结果进行了比较,如图3~图4所示。从图中我们可以看出,非线性最小二乘方法的估计误差明显小于线性最小二乘方法。但是,同时仿真也发现,非线性最小二乘方法受初始点设置的影响较大,当初始值偏离真实值较大时,估计效果不好,甚至会发散;求解过程中还受到∂1、β、ε设置的影响。
5 结语
单站纯方位跟踪问题是水下目标跟踪中的重要研究内容之一。文章通过建立一个非线性最小二乘模型并对其求解来解决单站纯方位问题,对建模过程和求解方法给出了详细的过程与步骤。对于非线性最小二乘方法初始化困难的问题,可以采用观测者机动以后的线性最小二乘估计为该方法的初始值,需要进一步的深入研究。仿真结果表明,该方法优于四维线性最小二乘方法,估计精度有了较大提高,是一种有效的算法,对于潜艇实施隐蔽跟踪具有重要意义。
[1]Nardone,s.c.,Aidala,V.J.Observability criteria for bearings-only target motion analysis[J].IEEE Trans.AES-17,1981
[2]赵正业.潜艇火控原理[M].北京国防工业出版,2003
[3]Aidala,V.J.Kalman filter behavior in bearings-only tracking application[K].IEEE Trans.AES-15,1979(1)
[4]Aidala,V.J.,Nordone,S.C.Biased estimation properties of the pseudolinear trackingfilter[J].IEEE Trans.AES-18,1982(7)
[5]Aidala,V.J.,Hammel,S.E.Utilization of modified polar coordinates for bearings-only tracking[J].IEEE Trans.AC-28,1983
[6]陈宝林.最优化理论与算法[M].北京:清华大学出版社,2005
[7]罗浩,赵厚奎,杨津骁.一种解决纯方位跟踪问题的新的最小二乘模型[J].火力指挥与控制,2008,33(11):137~139
