LTE中的Rijndael算法研究*

吴云梅，李小文，刘丹丹

（重庆邮电大学 通信学院，重庆 400065）

责任编辑:孙 卓

1 引言

自20世纪70年代以来，被广泛使用的数据加密标准（DES）日益不能满足人们对数据安全性的需求。2000年10月，美国国家标准和技术研究所（NIST）经过多次评估，确定Rijndael算法为美国高级加密标准（Advanced Encryption Standard，AES）[1]，代替使用了 20 多年的 DES。如今该标准已在LTE系统中多处使用，其中在非接入层初始密钥的形成过程中[2]，使用了7次的Ek核就是Rijndael算法，只是每次使用的明文和密钥矩阵都不同。另外，非接入层和接入层的完整性保护算法（128-EIA2）与加密算法（128-EEA2）都是基于AES的Rijndael算法[3]。

2 Rijndael算法介绍

Rijndael算法中的许多运算是按字节为单位定义，1 byte可以看作是有限域GF（28）中的一个元素，由b7b6b5b4b3b2b1b0构成的字看作是多项式b7x7+b6x6+b5x5+b4x4+b3x3+b2x2+b1x+b0，其中 bi∈GF（2），0≤i≤7，bi为 0 或1。算法中涉及的运算主要有两种:

1）2个多项式的加法运算

定义为:相同指数项的系数和再模余2，即异或运算。例如，（x7+x5+x4+x3+x+1）+（x6+x5+x4+x2+x）=x7+x6+x3+x2+1。

2）2个多项式的乘法运算

多项式相乘之后的结果很容易造成溢位，解决溢位的方式是把2个多项式相乘的结果再模余1个不可约多项式 m（x）。 在 Rijndael算法中，该多项式为 m（x）=x8+x4+x3+x+1。例如，（x7+x4+x3+x2+x）mod（x8+x4+x3+x+1）=x7+x4+x3+x2+x。

3 Rijndael算法原理

3.1 Rijndael算法外部结构

Rijndael算法的外部输入由明文比特流和密钥比特流两部分组成，输出为密文比特流，如图1所示。明文比特流映射到4×Nb的状态矩阵中，密钥比特流也是一个4×Nk的矩阵。在Rijndael算法中，运算的轮数Nr由Nb和Nk决定，轮数的变动关系如表1所示。在当前的LTE系统中均采用128 bit明文和128 bit密钥的分组方式，即Nb=4，Nk=4，所以执行的轮变换次数为10次。笔者将以LTE系统中使用的Nb=4，Nk=4的分组方式说明。

表1 Rijndael算法中Nb，Nk与Nr之间的关系

3.2 Rijndael算法内部数学模型

算法的核心是轮运算，中间每轮运算由字节替代变换（SubByte）、行移位变换（ShiftRow）、混合列变换（Mix-Column）、轮密钥加（AddRoundKey）组成，但终结轮（Final Round）运算没有混合列变换。笔者以一轮加密过程为例分析其数学模型。

3.2.1 字节替代变换

字节替代变换是Rijndael算法中唯一的线性变换。它是一个砖匠置换，该置换包含一个作用在状态字节上的S盒。该S盒由有限域GF（28）上的乘法逆和仿射（Affine）运算构成。在有限域GF（28）上求逆运算保证了S盒的非线性。有限域GF（28）上的乘法逆运算定义为

用a-1进行仿射运算可得到字节替换的最终结果为

3.2.2 行移位变换

在行移位变换中，中间状态矩阵第1，2，3，4行分别循环左移 0，1，2，3 位，如图 2 所示。

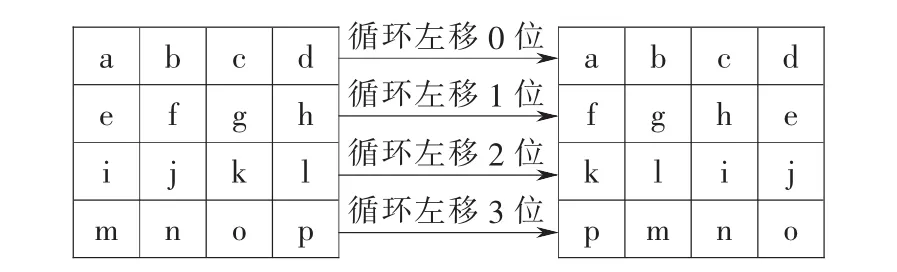
图2 状态矩阵行移位变换示意图

3.2.3 混合列变换

混合列变换是把状态矩阵中的每一列看作GF（28）上的多项式s（x）与一个固定多项式c（x）作乘法运算，如果发生溢位，则再模余 x4+1，表示为 c（x）={03}x3+{01}x2+{01}x+{02}，c（x）与 x4+1 互质，以矩阵乘法表示为

式中:0≤c≤3。

3.2.4 轮密钥加

经过混合列变换的状态矩阵与密钥矩阵按位异或（符号为⊕），根据加密的轮数使用相应的扩展密钥矩阵，具体为

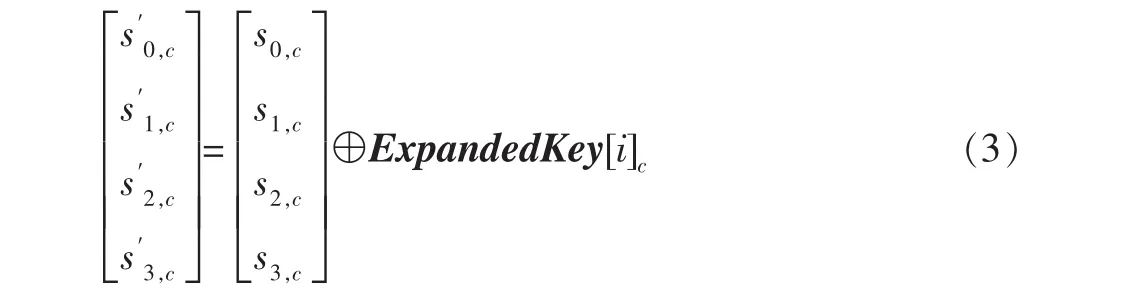
式中:0≤c≤3，ExpandedKey[i]c为第 i轮扩展密钥矩阵的第c列。

4 Rijndael算法加密/解密的实现

根据LTE系统中使用的Nb=4，Nk=4的分组方式，笔者设计的Rijndael算法加密流程图如图3所示，首先是4×4的状态矩阵与4×4的初始密钥矩阵按位执行异或运算，然后进行9轮迭代轮变换，每一轮的变换由字节替代变换、行移位变换、混合列变换、轮密钥加组成，终结轮变换不包含混合列变换。作为Rijndael算法的最终输出结果，密文比特流从经过加密处理的状态矩阵中由左至右按列输出。

图3 Rijndael算法加密流程图

基于图3的Rijndael算法加密流程设计出以下伪C代码描述的加密主程序为:

所以最终输出密文比特流就是Round[10]密文，再将得到的密文比特流作为解密过程的输入，得到相应的明文比特流，这样互相验证了加/解密过程的正确性。

5 小结

Rijndael算法的设计策略为宽轨迹策率（Wide Trail Strategy），提高抗差分攻击和线性攻击的强度。算法中各变换均为可逆变换，降低了解密过程的实现代价，字节替代变换起到混淆作用，提高差分均匀性，行移位和混合列变换都属于线性混合运算，确保多轮迭代运算的高度扩散性。Rijndael算法是将安全、高效、性能及灵活性集于一体，并且在不同的硬件和软件运行环境中都表现出始终如一的良好性能，这使它成为AES的合适选择。也正是因为这些优点，Rijndael在当前LTE系统中得到广泛的应用。

[1]NIST FIPS PUB 197，Advanced Encryption Standard-federal information processing standards publication[S].2001.

[2]3GPP TS 35.205， 3rd generation partnership project； technical specification group services and system aspects；3G security；specification of the milenage algorithm set:an example algori-thm set for the 3GPP authentication and key generation func-tions f1，f1*，f2，f3，f4，f5and f5*；Document 1:general[S].2002.

[3]3GPP TS 33.401 V8.5.0， 3GPP system architecture evolution；security architecture[S].2009.