电力应急事件处理中的数学方法论探讨

苗 新

（中国电力科学研究院，北京市，100192）

1 电力应急事件分类

电力应急事件包括突发事件及重大活动保电。突发事件是指突然发生，造成或者可能造成严重社会危害，需要采取应急处置措施予以应对的自然灾害、事故灾难、公共卫生事件和社会安全事件[1-6]。自然灾害指发生在地球表层系统，能造成人们生命和财产损失的自然事件，具有突发性、周期性、多因性、群发性、复杂性、潜在性，分为地质地貌灾害、气象灾害、生物灾害、海洋灾害，可以造成直接经济损失和人员伤亡、带来各种间接损失甚至影响社会稳定和持续发展。事故灾害指工矿商贸等企业的各类安全事故、交通运输事故、公共设施和设备事故、环境污染和生态破坏事故。公共卫生事件指传染病疫情、群体性不明原因疾病、食品安全和职业危害、动物疫情、严重影响公众健康和生命安全的事件。社会安全事件指严重危害社会、治安秩序的突发事件。按照社会危害程度、影响范围等因素，自然灾害、事故灾难、公共卫生事件分为特别重大、重大、较大和一般4级。重大活动包括重大国事、社会活动及体育比赛。电力应急事件的特点见表1和图1。

表1 电力应急事件特点Tab.1 Power emergent event features

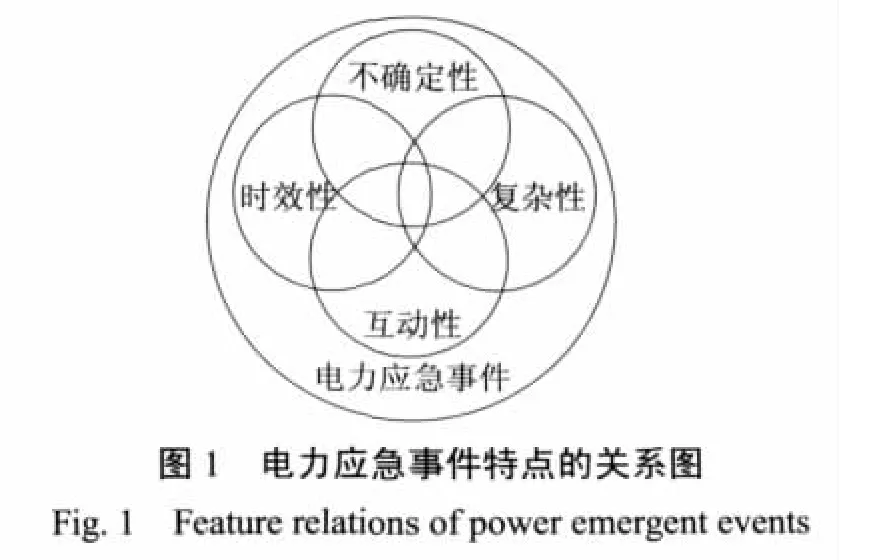
2 目前数学方法的局限性

目前，电力应急事件的应对包括预防与应急准备、监测与预警、应急处置与救援、事后恢复与重建等活动。其中使用的数学方法有解析法、概率法和历史模拟法等[2，5，6]。解析法是用常/偏微分方程组模型来处理，如用电网动态安全评估DSA(dynamic security assessments)静态模型动态数据的精确解来进行风险评估；概率法是用概率论与数理统计模型来处理，例如，用属于近似解的蒙特卡罗模拟概率评估法来进行风险评估；历史模拟法也用概率论与数理统计模型来处理，例如以历史时期所观测到的时序数据作为样本，求出时序数据之间差值，并按差值大小排序，根据所要求的风险水平确定置信度，最后计算出下一时序置信度范围内的风险评估概率值和预报值[5，8]。目前电力应急事件应对处理中使用的数学方法主要局限于确定解数学和随机数学范畴。

电力应急事件通常具有发生时间的不确定性、发生地点的不确定性、发生事件类型的不确定性、发生事件频率的不确定性、可能造成损失程度的不确定性，同时具有发生灾后灾（即次生、衍生、后续灾害）的可能性。虽然具有小部分确定性问题，但是相当多地存在随机性、模糊性、突变性等不确定性问题；所以，电力应急事件应对处理中使用的数学方法需要突破常微分、偏微分方程组模型——经典的确定解数学和概率论与数理统计模型——随机数学范畴局限，引入模糊数学与混沌数学方法[6-19]。

3 数学方法论改进探讨

基于对电力应急事件的分析，为了克服目前电力应急事件应对处理中使用的数学方法的局限性，本文从2个方面探讨了应对电力应急事件的数学方法：一方面引入模糊数学与混沌数学方法；另一方面引入5个维度空间处理相结合的方法，即将电力应急事件发生的时间、地点、类型、频率和损失程度共5个方面设定为5个维度的空间来处理，见表2。针对某具体电力应急事件，使用该方法的过程如下。

表2 数学处理方法Tab.2 Mathematical treatment method

首先，从5个维度分别分析。第1维度：发生时间不确定性采用概率论与数理统计方法来分析和预测其随机性；第2维度：发生地点不确定性采用概率论与数理统计方法来分析和预测其随机性；第3维度：发生事件的类型不确定性采用模糊数学方法来分析和预测其模糊性；第4维度：发生事件的频率不确定性采用概率论与数理统计结合模糊数学方法来分析和预测其随机性和模糊性；第5维度：可能造成的损失不确定性采用模糊数学和混沌数学方法来分析和预测其模糊性和突变性。

其次，综合以上5个维度，构造一个状态空间，建立该电力应急事件的数学模型，通过软件算法实现，进而模拟仿真该电力应急事件。

确定性、随机性、模糊性和突变性之间的关系见图2[5-15]。

确定性也称为必然性，其实质是一因一果的因果决定性，即在一定条件下必然会出现某种确定的结果，可以采用经典数学手段来研究，其表述形式有3种：集合至集合的映射关系、集合至数域的泛函关系及数域至数域的函数关系。例如，用常微分、偏微分方程组可以求出精确解的解析法。

随机性又称为偶然性，是指因为事件发生的条件不充分，使得条件与结果之间没有决定性的因果关系，在事件的出现与否上表现出的不确定性质，即在一定条件下可能会出现各种不同的结果，因果律破缺而导致一因多果。可以用随机数学作为工具对其进行研究。将“随机性”用“概率”予以量化表示，借助于随机变量的分布函数，可以研究随机现象的全部统计特征。贝叶斯理论利用先验知识和样本数据来获得对未知样本的估计，而概率是先验信息和样本数据信息在贝叶斯理论中的表现形式，因此，贝叶斯理论使得随机性的不确定知识表示和推理在逻辑上非常清晰并且易于理解。带可信度的不确定推理，引入信任函数和似然函数来描述命题的不确定性，当先验知识很难获得时，可以区分不确定和不知道的差异。

模糊性又称非明晰性，它的出现是由于概念本身模糊。一个对象是否符合这个概念难以确定，在质上没有明确含义，在量上没有明确界限，这种边界不清的性质，不是由人的主观认识造成的，而是事物的一种客观属性。概念外延的不确定性质，实质是排中律破缺、概念外延的不分明性，具有“亦此亦彼”的模糊性，可以用模糊数学作为工具来研究。模糊集合论引入了集合中元素对该集合的“隶属度”，从而将经典集合论里的特征函数取值范围由二值{0，1}推广到区间[0，1]，将经典二值逻辑推广至多值逻辑，使得模糊性可以用[0，1]的区间来度量。模糊性可以采用与随机数学平行的可能性理论表述，具体工具为模糊数学中隶属函数、模糊关系方程及模糊推理逻辑。

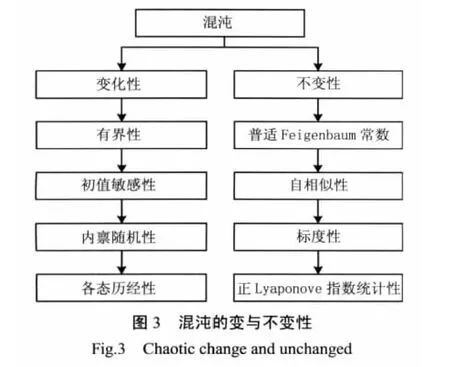
突变性又称为混沌，是不可预测、不可分解而同时还有规律性的成分，简单的个体遵循简单的规律，多个个体相互作用可以建立复杂和不可预测的行为，具有对起始条件的敏感性(即“蝴蝶效应”或积累效应)、不可预测性、遍历性、自我相似性等特征，可以用混沌(包括分形)数学作为工具来研究。混沌的不确定性由内禀随机性引起，表现为非定点、非周期运动。混沌的变化与不变性，如图3所示。混沌数学建模工具为离散映射，例如高维庞加莱映像[8-16]。

4 结论

为预防和减少电力突发事件的发生，控制、减轻和消除电力突发事件引起的严重社会危害，通过预防、预备、监测、预警、处置、恢复重建等环节应对电力应急事件，需要从数学方法论上突破经典数学和随机数学范畴的局限。

基于对电力应急事件的分析，为克服目前电力应急事件应对处理中使用的数学方法的局限性，从2个方面探讨了应对电力应急事件的数学方法。一方面引入模糊数学与混沌数学方法，另一方面引入5个维度空间处理相结合的方法，即将电力应急事件发生的时间、地点、类型、频率和损失程度等5个方面设定为5个维度的空间来处理，为进一步开展电力应急体系研究和建设工作提供数学方法论范畴的参考。

[1]全国人大常委会法工委国家法室.中华人民共和国突发事件应对法释义及实用指南[M].北京：中国民主法制出版社，2007：3-266.

[2]国家处置电网大面积停电事件应急预案[EB/OL].(2006-01-24)[2009-04-06]http://www.gov.cn/yjgl/2006-01/24/content_168998.htm.

[3]国家自然灾害救助应急预案[EB/OL].(2006-01-11)[2009-04-06]http://www.gov.cn/yjgl/2006-01/11/content_153952.htm.

[4]国家突发公共事件总体应急预案[EB/OL].(2006-01-08)[2009-04-06]http://www.gov.cn/yjgl/2006-01/08/content_21048.htm.

[5]Zhao Shuhong，Chen An，Rong Xiaoxia.Dynamic Game Network with Bayesian Rule and Application in Emergency Management[C].Proceedings of 20th Global Project Management Conference，2006：137-141.

[6]田世明，陈希，朱朝阳，等.电力应急管理平台研究[J].电网技术，2008，32(1)：30-34.

[7]Newton I.自然哲学之数学原理[M].王克迪，译.武汉：武汉出版社，1992：1-120.

[8]王梓坤.概率论基础及其应用[M].北京：北京师范大学出版社，1995：3-20.

[9]李洪兴，汪培庄.模糊数学[M].北京：国防工业出版社，1994：1-30.

[10]李德毅.知识表示中的不确定性[J].中国工程科学，2000，2(10)：73-79.

[11]Ruelle.机遇与混沌[M].上海：上海科技教育出版社，2001：3-50.

[12]苗东升，刘华杰.混沌学纵横论[M].北京：中国人民大学出版社，1993：1-30.

[13]王梓坤.论混沌与随机[J].北京师范大学学报，1994，30(2)：199-202.

[14]王兴元.复杂非线性系统中的混沌[M].北京：电子工业出版社，2003：1-90.

[15]韩传峰，叶岑.政府突发事件应急能力综合评价[J].自然灾害学报，2007，16(4)：149-153.

[16]金磊.中国西部开发与防灾减灾战略初论[J].系统工程，2000(4)：64-67.

[17]谢强.电力系统的地震灾害研究现状与应急响应[J].电力建设，2008，29(8)：1-6.

[18]苗新，陈希，张恺，等.应急与减灾信息通信系统国外研究现状[J].电网技术，2009，33(S1)：7-12.

[19]苗新，陈希，张恺，等.固定和移动网络相融合的近程电力应急通信网络 [J].电网技术，2009，33(S1)：22-26.