基于独立分量分析算法的脑电伪迹分离研究

【作者】应俊，陈广飞，何史林

解放军总医院生物医学工程研究室，北京，100853

盲信源分离(Blind Source Separation, BSS)是信号处理领域中的一个重要研究方向，在近些年来得到了飞速的发展，成为了研究的热点。对于盲信源分离，方法之一就是基于统计独立性的独立分量分析（Independent Component Analysis, ICA）方法，以高阶统计量为基础，是一种自适应优化算法，主要用于揭示和提取多维信号中的潜在部分，基本思路从多维观测信号中提取统计独立的成分。与传统的多维信号分析方法截然不同的是，经处理得到的各个分量不仅去除了相关性，还是相互统计独立的，并且是非高斯分布的信号。独立分量分析是一种性能优良的盲信源分离技术，在知道很少的信号先验知识的前提下，能有效地把信号的独立成分分离出来。

脑电（EEG）是一种反映大脑活动的微弱生物电信号，由于脑电采集系统具有很高的时变敏感性，在脑电信号采集的过程中，极易收到外界干扰，几乎所有的导联都能记录到一些伪迹信号如工频干扰、EOG、ECG、肌电等。传统的脑电伪迹分析方法是从测量信号中去掉具有明显伪迹特征的记录（比如幅度的峰值、频率分析、方差和倾斜度等指标超过了给定的阈值）。这种简单方法可能导致大量数据丢失，特别是无法进行强眼动过程中的大脑活动的研究[1]。理论上认为脑电信号中的眼动伪迹、心动伪迹、肌电信号以及其他干扰源所产生的干扰信号都是由相互独立的信源产生的[2]。而通过ICA 分解便可以去除伪迹而保留有用的脑电信号，ICA方法的应用是将脑电信号和伪迹信号分解成一系列相互独立的分量，通过一定的判断准则，去除伪迹干扰，再经过逆运算还原成脑电信号。

2 ICA算法基本原理

2.1 基于脑电信号采集的ICA数学模型

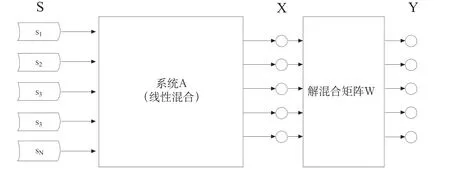
图1 ICA问题示意图Fig.1 Schematic diagram of ICA issue

设向量X=[x1(t)，x2(t)，…，xN(t)]T是用t时刻N个脑电头皮电极阵列测得的N维观测信号，S=[s1(t)，s2(t)，…，sN(t)]T是产生观测信号的N个相互统计独立的源信号，在采集的原始脑电信号中，源信号除了包括真实脑电信号与各种伪迹，则观测信号向量X是S通过未知系统混合矩阵A线性混合产生，即X=AS。ICA所要解决的问题是在S和A未知的情况下，寻找M×N维解混合矩阵W，得到M维向量Y=WX，使得Y逼近源信号S。要应用上述ICA问题模型，采集的脑电信号必须满足如下条件：

(1) 脑电信号与伪迹均为平稳随机过程，且相互独立。脑电信号是由大脑皮层神经元活动产生，而眼活动、肌肉活动、工频干扰等信号是通常不受脑活动限制，所以认为是相互独立的信号源；

(2) 混合矩阵A是列满秩，即采集过程中保证所有传感器采集的信号均是源信号的线性混合；

(3) 源信号的数目不大于传感器的数目，即M≤N。在多导脑电中，主要伪迹信号源少于传感器个数，为便于计算，一般ICA算法都假设M=N；

(4) 信号混合不考虑噪声影响，脑电伪迹分析中暂不考虑采集过程中的噪声。

2.2 ICA的分量判断准则

ICA的思路来自于中心极限定理，根据中心极限定理，一组均值和方差为同一数量级的随机变量共同作用的结果必接近于高斯分布。因此独立分量的线性叠加的分布，如以高斯分布为参考，则观测信号往往比原始分量的分布更接近高斯分布，或者说源信号的非高斯性比观测信号的非高斯性要更强，可将分量的非高斯性作为独立性的判据，各分量越接近独立，非高斯性越强，因此，可以对分离结果的非高斯性进行度量，当其非高斯性达到最大时，就可以认为实现了最佳分离。独立分量分析中采用的非高斯量度主要有峭度及负熵。在脑电伪迹分析中，我们以最大负熵作为分量评判准则，采用固定点算法（又称Fast ICA）顺序实现独立源分量的提出。

2.3 Fast ICA算法与实现

Fast ICA是一种基于非高斯性极大化原理[3]的算法，采用批处理的方法，在每一步迭代中大量样本数据参与运算，Fast ICA在众多ICA算法中具有收敛更快速、稳健的特点。Fast ICA目标在于寻找一个合适的解混合矩阵W使得各自的负熵最大，由于负熵的计算较为复杂，难以直接获得。Hyvarinen[4]给出了负熵的近似表达式（随机变量假设为零均值且具有单位方差）：

式中，v是具有零均值且与y具有相同单位方差的高斯随机变量，G(●)是非二次函数，通常取logcosha1y（其中1≤a1≤2），等非线性函数。基于如上的近似函数，Hyvarinen[3][5]给出Fast ICA迭代公式：

式中，g(●)是G(●)的一阶导函数，z是对数据进行白化预处理后的结果，W是解混合矩阵。

3 ICA脑电伪迹分离中的应用

3.1 算法结构

脑电伪迹分离的过程首先要通过Fast ICA来对脑电信号进行独立成分的分离，再通过多种特征的综合分析，判断出伪迹分量，最后将伪迹消除后，重新恢复脑电信号。算法的核心在于ICA分离独立成分，设计Fast ICA算法流程如图2：

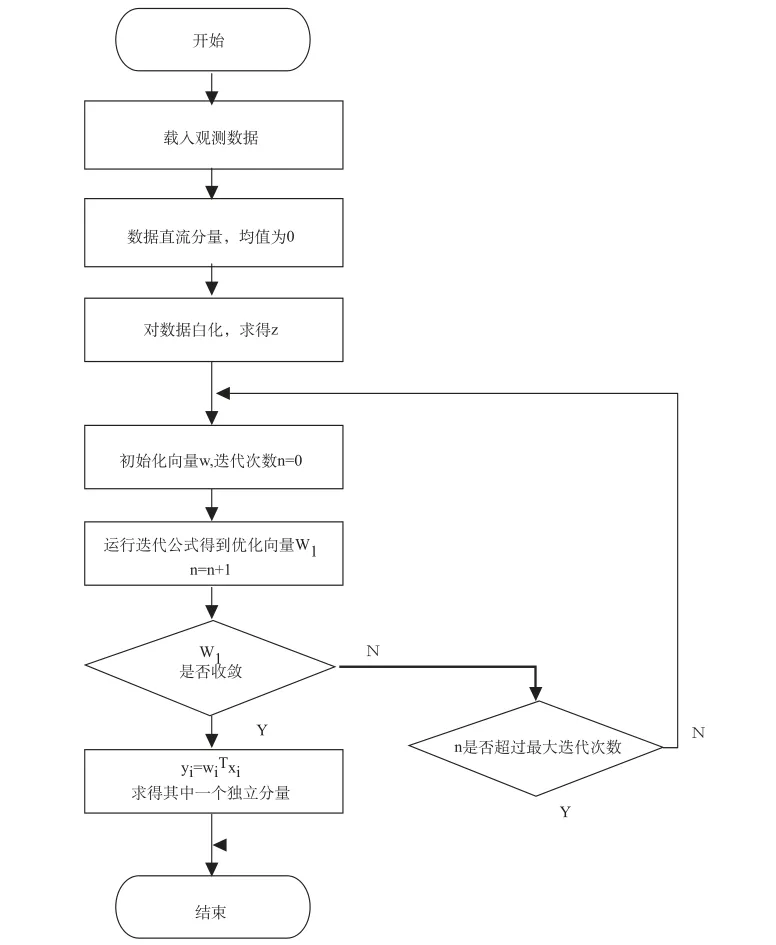
图2 单次分离Fast ICA算法流程图Fig.2 Flow chart of single separation in Fast ICA arithmetic

算法最后得出的权值向量wi意味着分离了混合信号xi中的一个非高斯信号，(i =1,2,…)等于分离出的一个独立成分。该算法的一个显著的特性是它的收敛速度非常快，一般迭代5～10次即可收敛。为了估计n个独立成分，必须运行上面的算法n次，依次迭代出权值向量，从而求出了ICA的分离矩阵W的行向量。每次迭代提取一个新的独立分量时，为避免新迭代出的wi+1，与已求出的前i个权值向量收敛到相同的方向，必须保证新独立分量所对应的分离矩阵行向量与已求出的分离矩阵其它行向量相互正交。因此，在迭代新向量wi+1时，必须为其进行去相关处理。相应的计算公式如下：

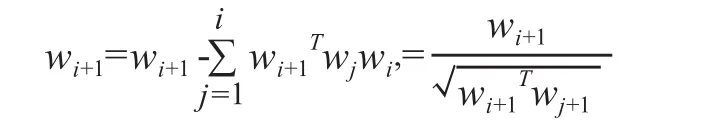
通过Fast ICA算法求得各独立分量之后, 消除伪迹干扰的方法是将干扰成分独立分量置零, 其他分量保持不变，再由W-1映射到各电极处得到不含伪迹干扰的脑电信号。

3.2 眼电伪迹消除实验

3.2.1 Fast ICA分离结果

眼电伪迹一般都会随机地出现在脑电信号中，且幅度比正常脑电信号大，脑电信号因为眼电伪迹的干扰而影响分析。本实验采用的脑电数据来源于解放军总医院脑电图室提供的临床实测国际标准32导脑电图数据，测量对象处于安静闭目状态，测试过程中我们要求受试者做动眼运动。数据采样率512 Hz，采样时间为10 min，从中截取200 s作为ICA分析的样本。原始脑电图如图3所示，发生眼动时，所有信号均受到不同程度的影响。脑电信号经过Fast ICA分离，所得32个独立分量如图4所示。

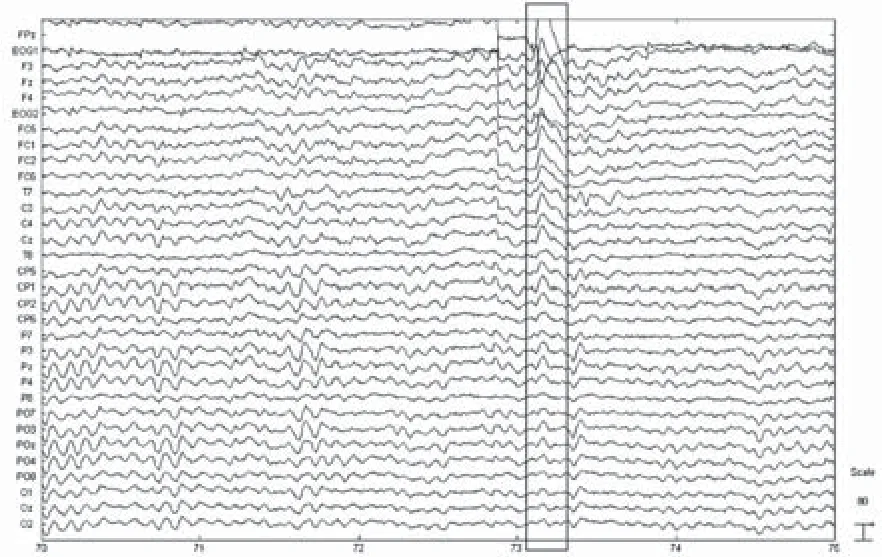
图3 含有眼动伪迹的脑电图Fig.3 EEG signal with EOG

图4 含有眼动伪迹的脑电图Fast ICA分离结果Fig.4 Result of separated EEG with EOG by Fast ICA

3.2.2 伪迹分析

判断伪迹需要大量的临床经验，通常的标准为以下几个方面：在独立分量地形图的位置属于脑相关的活动区域；功率谱分布上，符合典型的脑电信号特征；时域波形特征。基于以上3点，我们分析得出图4中，第3分量为眼电伪迹，理由如下：

(1) 从时域上判断，第3独立分量波形一般比较平缓，其他分量均呈现脑电特征的正弦样波动，在原始信号出现明显眼动干扰的时间点附近，第3独立分量出现幅度较大峰值。

(2) 从功率谱上判断，由于测试对象处于平静清醒闭眼状态下，整个皮层均产生8-13 Hz左右的α波，从其他分量频谱分析，在8-13 Hz表现出明显的峰值，而第3独立分量频谱在相应区域未出现明显的峰值，比较符合眼动伪迹的功率谱特征。

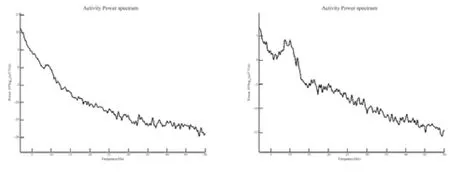
图5 眼电伪迹分量与正常脑电分量功率谱图Fig.5 Power spectrum chart of EOG artifacts and normal EEG

(3) Fast ICA运算过程中所得的逆矩阵W-1的列向量表示各独立分量在头皮电极处的投影强度。根据W-1的列向量绘制的脑地形图提供我们关于源信号位置的信息，其也可以用于检查生物学方面的合理性。第3独立分量的脑地形图如图6，其信号源能量主要集中于脑的前额部位，符合眼活动生理特性。

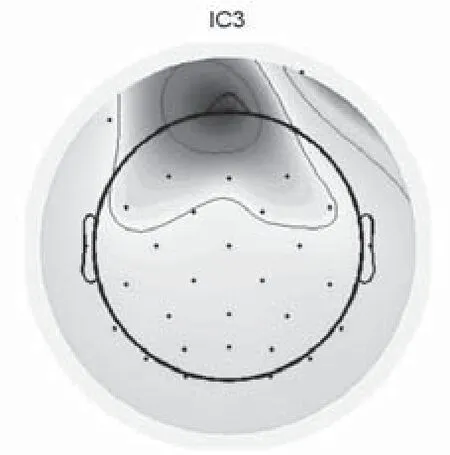
图6 眼电伪迹分量脑电地形图Fig.6 Brain electrical activity mapping of EOG component

3.2.3 伪迹分离与脑电信号复原

确定第3分量为眼电伪迹后，将该分量数值全部置零,再由W-1映射到各电极处，复原脑电信号。该做法的实质是从观测信号中取消眼电伪迹源对各个电极处的贡献，这一思想在脑电的其它各种伪迹去除中也广泛适用。如图7所示，将消除眼电伪迹的脑电信号（红色）与原始信号（黑色）进行对比，使得信号从时域上观察更加平滑。

3.3 脑电工频干扰抑制实验

随着EEG中高频信号在评估认知功能中的应用，重叠了50Hz 工频噪声的脑电信号也不能简单地用线性滤波器去除，ICA算法可实现将工频干扰作为独立分量从脑电信号中分离。本实验采用的脑电数据来源于自行研发的脑电信号采集系统采集的16导脑电图数据，测量对象处于安静闭目状态，数据采样率512 Hz，以其中200 s作为ICA分析的样本。原始信号如图8所示，从时域上看，原始信号受到50 Hz工频干扰，出现大量规则的正弦波形。通过对信号进行功率谱分析，在50 Hz左右出现峰值，高于脑电中α波的幅度。

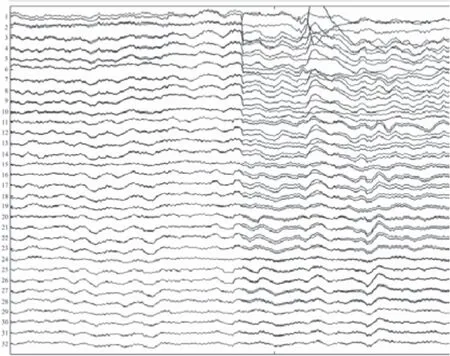
图7 消除眼电伪迹后的脑电图Fig.7 Result of removing EOG artifacts from EEG

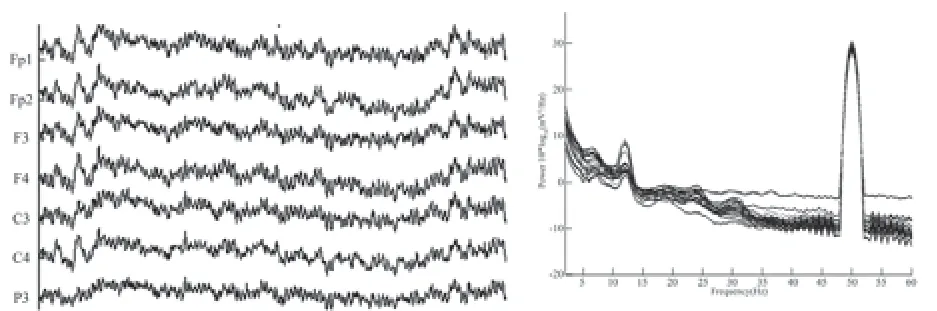
图8 部分含有工频干扰脑电波形图与功率谱图Fig.8 Partial EEG signal with power line interference and power spectrum chart

通过Fast ICA分离之后，通过时域波形、功率谱与脑电地形图的分析，判断得出其中第2分量为50 Hz工频干扰。时域波形如图9所示，第2分量明显呈现规则的50 Hz交流信号。通过对第2分量进行功率谱分析，发现其在50 Hz的峰值接近于原始脑电信号功率谱中50 Hz左右峰值的大小。由于工频干扰的引入受到环境信号源与采集系统本身的影响，每个脑电传感器受到工频干扰的影响程度没有明显差别，所以在第2分量的脑电地形图上没有表现出信号源位置的差异性，如图10所示，50 Hz在整个脑部皮层的影响均很大。确定第3分量为工频干扰后，按照消除眼电干扰的方法，我们将第3分量清零，重新复原脑电信号。如图11所示，脑电波形图中，深色表示分离之后复原的脑电信号，浅色表示原始信号，消除工频干扰之后的脑电信号细节较好的保留下来，这点在功率谱分析中得到证实。消除伪迹前后功率谱分析中50 Hz左右的幅度显著减少，8～13 Hz左右的脑电α波功率谱没有变化。

图9 含有工频干扰的脑电图Fast ICA分离结果Fig.9 Result of separated EEG with power line interference by Fast ICA

图10 工频干扰分量脑地形图Fig.10 Brain electrical activity mapping of power line interference component

图11 消除工频干扰后的脑电波形图与功率谱图Fig.11 EEG signal and power spectrum chart after removing power line interference

3 结论

独立分量分析技术作为一项新的信号分解技术，经历10余年的发展，其在生物医学、模式识别、雷达信号处理等众多领域引起人们的关注。实验证明，ICA 算法的分离技术在脑电伪迹分离问题上有着很好的解决方法，具有独特的优越性，特别在分离含有显著独立分量干扰的混合信号。但随着ICA 算法理论的不断完善与推广，ICA方法将成为脑电信号增强及脑电特征提取的有效的分析工具。

[1]周宗潭, 董国华,徐昕, 等.独立成分分析[M].北京:电子工业出版社,2007:286-287.

[2]杜晓燕,李颖洁,朱贻盛,等.脑电信号伪迹去除的研究进展[J].生物医学工程学杂志.2008.25(2).465-466.

[3]Hyvarinen A, Oja E.Independent component analysis: algorithms and applications[J].Neural Networks.2000,(13):411430.

[4]Hyvarinen A.Fast and Robust Fixed-Point Algorithms for Independent Component Analysis [J].IEEE Trans Neural Networks, 1999, 10(3): 626-634.

[5]Hyvarinen A.New approximations of differential entropy for independent component analysis and project pursuit[J].Advances in Neural Information Processing System, vol.MIT Press,1998.10, :273-279.