一种无可信第三方的认证协议研究

王杰 司志刚

解放军信息工程大学电子技术学院 河南 450004

0 引言

身份认证是一种重要的安全技术，也是保证系统安全的第一道防线。用户在使用系统之前，要求通过身份认证系统识别身份，才能得到授权访问系统资源。在分布式系统中，特别是在移动台与网络之间的无线接口是开放的情况下，使得攻击者有窃听和冒充合法用户的机会，所以对使用者的身份认证是非常重要且必不可少的。

1984年，Shamir首次提出了“基于身份的密码方案”，该方案仅仅支持数字签名，而不支持消息加密。Tsujii提出了一种新的基于身份的密码方案，该方案是基于离散对数问题的困难性，它能抵抗共谋问题，但需要高次幂运算。Okamoto和Tanaka扩展了Shamir的思想，他们结合数字签名和密钥分发，提出了一种简单的基于身份的密码方案，该方案不仅支持消息加密，而且能抵抗共谋问题。但是，该方案存在一些缺陷，用户认证可能被伪造，用户秘密信息可能暴露出去，并且需要较高次的幂运算。

我们提出一个新的认证协议，密钥管理中心(key management center,KMC)只是在建立安全网络系统时或者有新成员要求注册加入时才需要，而在其他任何时候它的存在都没有作用，也就是说我们不需要可信的第三方(密钥管理中心)。我们的协议不仅减少了指数运算的次数，而且解决了Okamoto和Tanaka方案中出现的安全问题。

1 无可信第三方的安全认证协议

本文的安全认证协议用到了基于 ID的认证方案和对称密码技术。基于 ID的认证方案用于系统建立和认证，而对称密码用于后来的消息认证以获取更好的通信性能。新的认证协议有两个阶段：初始化阶段在KMC 建立系统时完成，而认证阶段在通信双方完成双向认证和交换共享会话密钥时结束。

1.1 初始化阶段

密钥管理中心既不负责双向认证也不负责产生共享密钥，它的角色只是简单地为新注册用户产生公开的和秘密的信息。当建立安全网络系统时，KMC需要执行以下步骤：

(1) 选择两个大素数p和q，并且使npq=⋅。

(2) 通过以下计算，获取密钥管理中心的秘密信息d，这里d只有密钥管理中心知道：

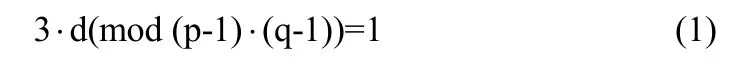
(3) 找到一个整数g，g是有限域 GF(p)和 GF(q)的生成元，这里g是密钥管理中心的公开信息。

(4) 用IDi表示要求注册到这个安全网络中的用户i的身份，它秘密存储于用户身份卡(IC卡、SIM卡、UIM卡、TF卡等)中，iID由姓名、部门、地址等组成。

(5) 选择一个单向函数f计算 i的扩展身份(EIDi):EIDi≡f(IDi)(mod2N)

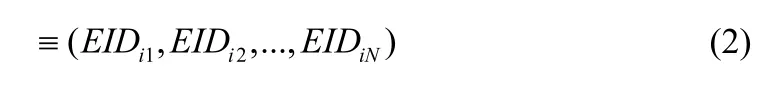
这里N表示EID的二进制长度。

(6) 计算EIDi后，生成用户的秘密信息Si：

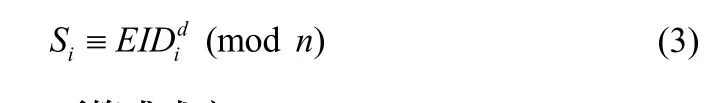
从上述可知，下等式成立：

(7) 通过一个安全通道把(n,g,f(x),Si)返回给用户i，用户i必须使Si保密，并且存储(n,g,f(x))。

一旦安全网络系统建立起来，除非有新用户加入，将不再需要KMC。KMC必须秘密地存储，以便以后使用。然而，整数p和q不再使用并且要秘密地销毁。当一个新用户要求加入时，他把自己的ID发送到中心。收到用户ID之后，中心重复步骤(5)至(7)。

1.2 认证阶段

新的认证协议只需要两条消息就可完成双向认证。从用户i收到第一条消息之后，用户j验证消息的内容。如果验证成功，他就相信这条消息是用户i发送的。这样用户j完成了对用户i的认证。同样，用户i通过第二条消息完成对用户j的认证。一次会话的双向认证和密钥交换的执行步骤如下：

(1) 如果用户i希望与用户j通信，产生一个随机数ri，并且计算下面两个整数：这里timei是他计算出两个整数的时间。

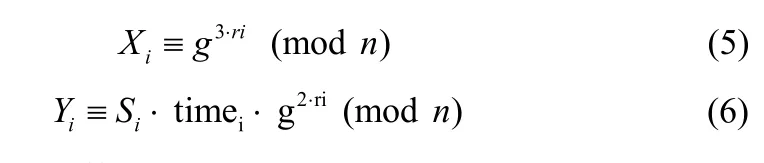
(2) 用户i把(Xi,Yi,IDi,timei)发送给用户j。

(3) 收到消息之后，用户j把timei与当前本地时间相比较，如果timei和当前本地时间的差异比有效周期短，收到的消息被认为是有效的。根据不同的网络环境，有效周期的长度可以调整(在时钟不同步的网络中，为了避免有效的消息被拒绝，timei与当前本地时间对比的步骤应当跳过)。然后用户j计算EIDi=f(IDi)，并检查下面的等式是否成立：

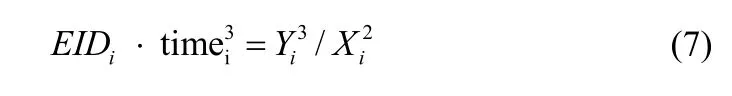
(4) 如果等式成立，用户j认为消息是用户i发送的，并且保存Xi，以便以后产生共享秘钥。接下来，用户j产生一个随机数rj，并计算下面两个整数：

(5) 用户j把(Xj,Yj,IDj,timei)发送给用户i。

(6) 用户i收到消息之后，检查timei是否与他之前发送的一样(在这里，timei可以看作用户i的一个因数，它只用了一次)。如果一样，他计算EIDj=f(IDj)，并且检查下面等式是否成立：

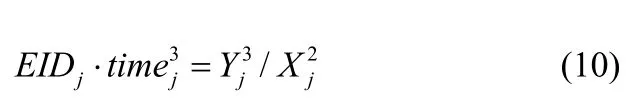
(7) 如果成立，用户i计算会话密钥Kij如下：

(8) 同样地，用户j计算会话密钥Kji如下：

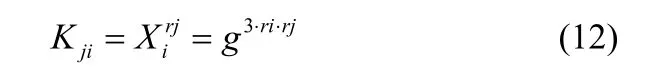
(9) 用户i和j用Kij=Kji作为这次会话的共享密钥来加密通信信息。

2 计算量

在Okamoto和Tanaka的方案中，为了完成双向认证和交换共享密钥，一次会话每一方需要五次幂运算(一次用于Xi，一次用于 Yi，两次用于等式检查，一次用于共享密钥计算)。

我们的协议把每次通信会话的幂运算次数从五次减少到两次。在认证阶段，我们可以首先计算出gri，然后按下面计算出Xi和 Yi：

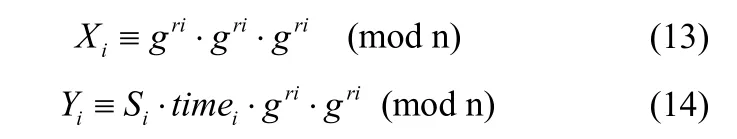
在这两个方程中，只需乘法运算，没有幂运算。同样，验证发送者的身份不需要幂运算就可以完成。所以，我们的协议只需要两次幂运算(一次用于gri，一次用于共享密钥(Xi)ri)。

3 安全分析

为了保证通信网络的保密性和安全性，我们的协议提供消息加密和通信双向认证。它不存在Tsujii方案中的共谋问题，因为它的安全性依赖于计算离散对数问题的难度。如果一个冒充者想假装用户i和其他人通信，他必须找到两个整数x和y满足下面的等式：

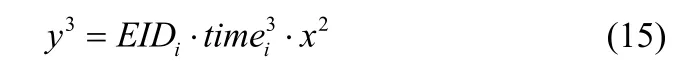
在这个等式中使用小的公共指数没有减少破解(x,y)的难度。尽管冒充者能得到一个整数对(y3,x2)使这个等式成立，但是整数对(x,y)是很难得到的，因为从(y3,x2)计算(x,y)是一个离散对数难题。

我们的协议也可以保护用户免于Hastad攻击。Hastad在1985年提出一种公共主干网络中使用RSA低次幂运算的攻击方法。为说明这种攻击方法，举例如下：假设消息m被广播给三个终端，这里的三个公开幂指数是： e1=e2=e3=3，模分别是 n1，n2和n3，加密的消息分别是：m3mod n1，m3mod n2，m3mod n3。根据中国剩余定理，我们可以得到m3mod n1n2n3。然而，m3＜n1n2n3，因为m＜n1n2n3。因此，m3不会因为减小模 n1n2n3而受到影响，消息可以通过计算m3的立方根而获得。这种攻击在我们的协议中就不能成功，因为所有的通信方使用相同的模数n。

尽管我们使用时间表检验消息的合法性，即使假设不存在同步时钟，重放攻击在对我们的协议也不会成功。考虑以下情况：入侵者窃听了一次消息会话，比如，用户i和用户j之间的消息。入侵者可能重放在以前的会话中捕获的旧的认证消息，收到旧的消息之后，用户j检验timei的合法性。如果系统时钟是同步的，通过检验timei知道这条消息是不可用的，所以丢弃这条认证消息。如果系统时钟没有同步，重新考虑这条消息，然后选择一个新的随机数rj'，回复入侵者以下消息：

然而这次会话的共享密钥是K'=g3⋅ri⋅rj'，而不是旧的共享密钥K=g3⋅ri⋅rj。不知道随机数ri，入侵者不可能计算出新的共享密钥K'。因为旧的消息都是用旧的共享密钥K加密的，所以入侵者不能成功重放他窃听到的旧消息。用户 j可能试图用新的共享密钥K'解密重放的旧消息，但是解密失败。因此，关闭连接，从而攻击失败。

我们的协议也没有Okamoto方案中出现的两个弱点：

(1) 我们的协议使用两个小素数3和2代替Okamoto方案中的两个整数e和c，因为e是c的一个因数的可能性不再存在，所以在我们的协议中的用户秘密信息不可能透露。

(2) 因为使用单向函数f(x)，在我们的协议中伪造认证消息将会失败。如果一个恶意用户想给用户j发送一个伪造的消息，随机选择一个数对(X',Y')。尽管一个伪造的EID '可能通过(15)式计算出来，但不可能从EID '中获取正确的ID'，因为单向函数f(x)求逆的过程非常困难。如果随机选择一个身份信息ID ''，和(X',Y')、写消息的时间以及伪造的消息一起发送，用户j收到信息包后，将会从f(ID'')得到EID ''，而不是EID '。从而，(7)式的验证就会失败，用户j就会拒绝冒充的请求。所以，我们的协议能使用户在通信过程中抵抗冒充请求攻击。

4 结论

本文提出了一种基于身份的认证协议，在协议中 KMC和存储公共信息的文档都不是必需的。一旦安全网络系统建立起来，认证和密钥交换可由有关双方独自处理，而不需要KMC。本协议解决了 Okamoto方案中出现的问题。即使在系统时钟不同步的情况下，它也能抵抗重放攻击。与Okamoto方案需要五次幂运算相比，我们的协议完成双向认证和密钥交换仅仅需要两次幂运算，所以大大降低了通信设备的负载。本协议在无线窄带网络环境下移动终端用户身份的认证中具有一定的应用价值。

[1]A.Shamir, “Identity-based crypto systems and signature schemes,” in Proc. Crypto-84, Santa Barbara, CA.1984.

[2]S. Tsujii, T. Itho, and K. Kurosawa.ID-based cryptosystem using discrete logarithm problem.Electron. Lett., vol. 23.1987.

[3]E. Okamoto and K. Tanaka.Identity-based information security management system for personal computer networks.IEEE J. Select. Areas Commun., vol. 7.1989.

[4]王玲玲,侯整风.无可信中心的可认证秘密共享协议.计算机应用.2007.

[5]J. Hastad.On using RSA with low exponent in a public key network. in Lecture Notes in Computer Science: Advances in Cryptology-CRYPTO’85 Proc.