无线传感器网络中基于采样的查询处理方法研究

宋春晖 赵洪刚

1 黑龙江农业工程职业学院信息学院 黑龙江 150088

2 黑龙江大学信息技术研究所 黑龙江 150080

0 前言

无线传感器网络产生大量的分布式感知数据，有效地掌握这些感知数据是传感器网络使用者的最终目的。在查询过程中最小化无线通讯数据量，将节约十分可观的能量，从而延长无线传感器网络的生命周期。因此，对感知数据查询处理技术的研究具有重要意义。

1 感知数据的查询处理

以前，对感知数据进行管理和处理是由应用程序来实现，这需花费大量的时间和精力，限制了无线传感器网络的发展。研究表明：可以用一套与传统设计方法不同的、以数据为中心的思想来解决上述问题。

感知数据查询处理系统包括两部分。即：运行在基站或计算机上的查询处理软件和运行在传感器节点上的传感器端软件。前者主要功能是查询解析、检查、进行查询优化并将优化后的查询以“多跳”路由方式分发到传感器网络中，然后收集感知数据并以“多跳”路由方式将数据返回到基站或计算机上。后者进行查询接收、查询处理、采样和通信等操作，是一组分层次的组件。

可将感知数据具体查询处理执行过程描述如下：

(1) 用户在查询处理界面指定查询任务。

(2) 查询处理模块获取用户输入信息，并进行查询解析及检查操作。

(3) 查询处理模块将解析、检查后的查询命令转化为一种内部结构交给优化器。

(4) 优化器对来自查询处理模块的查询命令进行基于查询代价的优化。

(5) 优化器从优化后的一组查询计划中选择代价最低的查询计划转化为具体的、即将被执行的查询语句。

(6)查询处理模块将上一步中产生的查询语句按照一定的路由策略通过网络管理器分发到各个节点。

(7) 节点按照查询处理请求收集感知数据，同时进行最大化的感知数据本地处理。

(8) 节点将处理后的数据沿查询分发过程建立的路由树传播给双亲节点。

(9) 双亲节点进一步将其转发或将其与自己收集并处理后的数据、或从其他子节点收集到的数据进行合并后再转发。

(10) 如此不断进行下去，直到基站收集到用户感兴趣的数据为止。

2 基于采样的查询方法

采样方法的本质是避免列举整个样本分布，通过在优化查询过程中列举大量样本来近似代替联合分布。优化的目的是在所有传感器节点感知数据值中尽量减少错误数量。

PROSPECTORGREEDY方法简单的通过一次贪心地增加获取的感知数据值的方式构建一个查询计划。首先要给出所有样本中每个传感器节点对最后查询结果的贡献的优先权。只要查询计划的能量消耗没有超出预算，算法会贪心的最大化挖掘传感器节点ui的 ∑SS[s,i]值，并扩张当前查询计划来获得传感器节点ui的感知数据值。

3 PROSPECTORPROOF算法及其优化

本节设计一种新的例证方法，它以自下而上的形式，通过传递一个附加值来校对返回值，从而提高算法的准确性。

3.1 参数说明

(1) 用S表示一个布尔样本矩阵，其含义与前文相同。

(2) 用ones(s)表示为第s个样本提供前k个感知数据值的一组节点。

(3) 用smallers(ui,uj)表示第s个样本中以节点uj为根的子树中的一组节点，这些节点的感知数据值要比节点ui上的感知数据值小。

(4) 用一个变量b(ei) 表示为网络中的每条边ei所分配的带宽。在此算法中，不需要变量α(ei)表示查询计划是否用到了ei这条边。原因是例证查询计划必须用到网络中的所有边，否则无法证明前一个感知数据值，因为任何未被例证查询计划访问的传感器节点都可能产生最大的感知数据值。

(5) 用一个整型变量 xs(ui,uj)表示当查询计划运行到第 s个样本时，传感器节点ui的感知数据值是否被节点uj证明，其中：ui∈desc(uj)。

(6) 用r表示根节点。

(7) 用sibling(ui,uj)表示一组传感器节点，这些传感器节点是uj的孩子节点同时又不是节点ui的祖先。

3.2 PROSPECTORPROOF算法

在传统的查询方法中，网络中的每一条边都被分配给一定的带宽b(ei)，指定节点ui所允许通过的最大感知数据量。节点ui将保证在分配的b(ei)个带宽中感知数据能够被返回，在以节点ui为根的子树中，大小为l的子集真正包含有前l个感知数据值。这时，称这l个感知数据值被节点ui证明。在例证计划执行过程中，每个节点ui都按照以下步骤执行：

(1) 从子树中收到返回值。节点 ui从其每个孩子节点 uj收到b(ei)个感知数据值，在这些值中，前k个感知数据值被节点uj证明。

(2) 排序。节点 ui将从其孩子节点中收集到的所有感知数据和它自身的感知数据值进行排序，选择出即将要被上传的前b(ei)个感知数据值。

(3) 证明感知数据值。考虑在前 b(ei)个中的、即将要被上传的每个感知数据值y，这个感知数据值被节点ui证明。

(4) 将感知数据值返回给双亲节点。前 b(ei)个感知数据值都要传递给节点 ui的双亲节点 parent(ui)。如果被节点 uj证明的感知数据的数量小于b(ei)，那么这个数量值也要被上传给其双亲节点；如果这个数量值不小于b(ei)，那么所有b(ei)个感知数据值也都假定已被证明。

这种优化节约了通讯所带来的能量消耗，这个来自子树的数量值极有可能证明它们所传递的所有感知数据，完全排除要从叶子节点传递这个值的必要性。

在上述执行过程的末尾，根节点返回一系列的感知数据值作为查询操作的结果，同时，这些查询操作的结果证明了它们中的前 'k个感知数据值在整个目标无线传感器网络中也是前 'k个感知数据值。实际上，被根节点返回的其他感知数据值可能在也可能不在前k个感知数据值中，但是对观察者来说，它们可能仍然有用。就是说，它们有助于构建一个更有效率的向上扫描查询计划，来找回遗漏的前k个感知数据值，下一步将研究这个问题。

下面的这个引理是直接描述例证查询执行计划的：

引理：在例证查询计划中，被某个传感器节点证明了的l个感知数据真正是以这个节点为根的子树中的前l个感知数据。下面用一系列的线性规划公式来表达在已分配带宽的例证查询执行计划中的优化问题。如下所示：

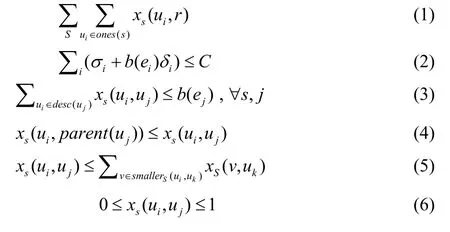
式(1)说明查询优化的目标是通过所有样本，最大化被根节点证明的前k个感知数据值中的数量。

式(2)指定查询计划的总的能量限制。发送被节点证明的感知数据的数量的能量消耗非常小，可以被适当地预算在非叶子传感器节点的固定的能量消耗中。

式(3)指明带宽约束限制。与PROSPECTORLP+LF算法相似。

式(4)说明任何一个感知数据值被某一传感器节点证明的约束，这个感知数据值必须被这个节点和拥有这个感知数据值的节点之间的所有传感器节点证明。

式(5)指明例证约束限制。也就是说，对于来自传感器节点 ui的感知数据值 y想被节点 uj证明，要求传感器节点 uj的每个孩子节点uk(除了上传出y的那个孩子节点)必须证明一些更小的感知数据值。

式(6)指明变量xs(ui,uj)的完整性约束。

本节论述的 PROSPECTORPROOF算法采用一个变量xs(ui,uj)代替了后者采用的 xs(ui)个变量而又没有降低算法的整体性能。该算法的查询结果要更为准确，但是它也存在着不足，即是前面提到的例外：当孩子节点uk真正返回以节点uk为根的子树中的所有感知数据值的时候，这些感知数据值中没有比y更小的了。针对这种情况可以对算法进行改进以提高其查询操作的准确性和算法的可用性。

4 改进的PROSPECTORPROOF算法

PROSPECTORPROOF算法虽然与前面的查询方法相比有很大提高，但是它在实际运行的过程中也存在一些例外，使得算法没有更好的可适应性。因此，可以对以上所述的算法进行改进，从其例外的条件开始改进算法，以使改进后的算法总能够返回更确切的感知数据值。

改进的算法的基本思想是利用PROSPECTORPROOF算法作为前一部分，如果传感器根节点能够证明所有前k个感知数据值，那么结束查询操作。否则，执行本算法的第二部分——“向上扫描”操作来重新查询被遗漏或未被证明的前k个感知数据值。

本算法第二部分的执行要依赖于第一部分运行所搜集的信息来缩小查询范围。最佳情况是第一部分产生合理的查询结果，这样第二部分执行起来将会变得十分容易甚至不需要执行第二部分。

假设及参数说明：

(1) 假定在第一阶段，每个传感器节点 ui记住了它自身的感知数据值和这个传感器节点的孩子节点所传过来的感知数据值。

(2) 用retrieved(ui)表示上述假设中节点ui所记住的一组感知数据值。

(3) 假设传感器节点 ui同样记住了这些感知数据值中被节点ui证明的感知数据值。

(4) 用proven(ui)表示传感器节点ui记住的感知数据值中被它证明的一组感知数据值。改进的 PROSPECTORPROOF算法主体：

在本算法中，将PROSPECTORPROOF算法作为第一部分，当第一部分的运行得到了观察者满意的结果时，本算法结束；否则，进入本算法的主体部分进行进一步的优化查询。现在研究改进算法的第二部分执行流程：

(1) 接收双亲节点的请求

传感器节点ui接收来自parent(ui)的一个三元组(l,ya,yb)，这个三元组的功能是请求网络中的传感器节点ui返回前一个感知数据值，请求返回的值要在ya和yb之间。

(2) 将要求发送给孩子节点

传感器节点 ui按照如下步骤构造一个查询请求(l’,ya’,yb’)：

①l'=l-|proven(ui)∩(ya,yb)|。传感器节点ui能够利用已经被证明的感知数据值来回复查询要求，这些值来自节点ui的双亲节点。只有剩余部分的查询请求需要被发送给它的孩子节点。

②ya'=max(ya,y)。其中 y是 retrieved(ui)∩(ya,yb)中的第l个感知数据值，如果这个值存在并且不是-∞的话。也就是说为了能在 ya和 yb之间，任何感知数据值至少必须比ya大才可以。

③ yb'=min(yb,min(proven(ui)))。传感器节点ui应该不需要向它的孩子节点请求任何比min(proven(ui))大的感知数据值，因为所有这些节点必须已经在 proven(ui)中。如果l’>0 并且 (ya,yb)≠φ，那么传感器节点ui就将这个请求以广播的方式发送给它的孩子节点。

(3) 接收并返回查询结果

如果传感器节点ui在前面的步骤中已经向其孩子节点发送了请求，它将会收到感知数据值并将这些值加入到retrieved(ui)中。最后，传感器节点 ui将retrieved(ui)∩(ya,yb)中的前一个感知数据值返回给它的双亲节点。

查询操作的启动过程如下：当感知数据值 y是retrieved(r)中的第k大的值时，根节点r以广播的方式启动本算法的第二部分，向其节点的孩子节点发送查询请求(k-k',y,min(proven(r)))，然后各传感器节点按照预先设定的规则执行此查询操作，并返回确定的查询结果。

5 总结

本文具体描述了PROSPECTORPROOF算法的实现。算法要求节点将收到的来自其子树的感知数据值和它自身的感知数据值排成一个有序序列。检查传感器节点ui能否证明每个即将要上传给双亲节点parent(ui)的感知数据值。如果即将要被节点ui上传的所有感知数据值都能够被节点ui证明，则直接将这些感知数据值上传，否则，将要被上传的感知数据值中被节点 ui证明的感知数据的数量值也上传给节点 ui的双亲节点。通过这个上传的数量值就能够证明它所传递的所有感知数据值，排除了从叶子节点传递这个值的必要性，实现了算法的功能又降低了整体通讯量。

本文提出的基于的PROSPECTORPROOF改进算法，以PROSPECTORPROOF算法作为第一部分，如果第一部分返回的值都已被传感器根节点证明，那么不需要此算法；否则，执行改进算法的第二部分。在改进算法的第二部分中利用了前一部分PROSPECTORPROOF算法中返回的被根节点证明的数据量，根据这个数据量以及返回的查询结果，确定一个三元组(l,ya,yb)，并将查询请求的消息从根节点开始广播到其各个孩子节点，直到返回了确切的感知数据值，本算法结束。改进的算法利用了前一算法产生的数据，将查询范围一步步缩小，最后得到理想的查询结果。新算法引入了本地过滤的查询策略，在传感器节点自身将感知数据过滤，大大减少了传感器节点间的通讯量，从而降低了算法的能耗。实验数据表明，在不影响数据精确度的情况下，系统能耗减少11.5%，算法具有很好的实用性能。

[1] 李建中.无线传感器网络专刊前言[J].软件学报.2007.

[2] Pottie GJ,Kaiser WJ.Wireless integrated newtork sensors.Communications of the ACM.2000.

[3] 李建中,李金宝,石胜飞.传感器网络及其数据管理的概念、问题与进展[J].软件学报.2003.

[4] Schurgers C and Srivastava MB."Energy efficient routing in wireless Network-Centric Operations:Creating the Information Force.Virginia:IEEE Communications Society.2001.

[5] Benjamin G, Deborah E, et al. DIFS:a distributed index for features in sensor networks. Proc. of the 1st IEEE Int’l Workshop on Sensor Network Protocols and Applications Anchorage.2003.

[6] Sylvia R, Brad K, Scott S,et al.Data-Centric storage in sonsomets with GHT.a geographic hash table.Mobile Networks and Applications.2003.

[7] Scott S, Sylvia R, Brad K,et al.Data-Centrie storage in sensor nets.ACM SIGCOMM Computer Communication Review.2003.

[8] A.Deshpande,C.Guestrin,S.Madden,J.Hellerstein,and W.Hong.Model-driven data acquisition in sensor networks[C].In Proc.of the 2004 Intl.Conf.on Very Large Data Bases.Toronto. Canada.Aug.2004.