等功耗编码算法的改进实现及抗功耗分析攻击研究

吴震，陈运，王敏，陈俊

（成都信息工程学院 信息安全研究所，四川 成都 610225）

1 引言

目前，各类基于功耗轨迹对密码设备进行分析攻击的技术发展迅速，从计时（TA, timing analysis）攻击[1,2]到简单功耗分析（SPA, simple power analysis）攻击[3]和差分功耗分析（DPA, differential power analysis）攻击[4]，现在又发展为地址差分功耗分析（ADPA, address-bit differential power analysis）攻击[5,6]等，此类攻击以其成本低、时间快等特点严重威胁着密码设备运行时的安全。

在目前流行的公钥算法或协议中，大多使用幂剩余运算作为其核心运算。针对该运算进行功耗分析攻击，可获取密码体制中密钥的部分信息，严重者可直接破译出密钥。

研究者根据功耗分析攻击特性提出的各种防范方案主要从减小可测量的功耗差异、时间差异或破除功耗、时间差异与取值间的相关性等方面入手，如门电路级的防范[7]、抗测量技术[8]、重编码技术[9]、随机操作技术[10]，但这些防范措施在公钥密码中的实现，结果是效率降低、功耗增加或电路面积变大。其中最令人无法忍受的是：公钥密码原本就比分组密码慢3个左右数量级，为了算法自身安全还要继续降低效率。

等功耗编码算法[11]运用香农信息优化理论，在保证甚至提高运算效率的前提下，同时获取较好的抗功耗分析攻击的能力，该算法的提出为公钥密码功耗分析攻击的防范研究提供了新的发展方向。

本文对等功耗编码算法的优化改进及快速实现进行讨论，并就真实硬件环境下该算法的功耗信息泄露进行深入分析，其研究成果对其他公钥算法（如ECC椭圆曲线算法）也有借鉴意义。

2 幂剩余运算的BR实现算法

基于有限域上幂指数和离散对数的公钥密码体制，其核心运算有如下数学形式：

为保证密码学上的安全性，式(1)中的各参数均采用大整数，如K、N的取值在1024bit以上，采用直接计算的方法对硬件设备要求极高，同时效率低下，在实践中，一般采用一种迭代算法，称为二元表示法(BR, binary representations)[12]。其他快速算法几乎都建立在BR算法之上。

BR算法的具体实现形式有：从左至右(L-R)、从右至左(R-L)、左右混合或称随机指数(RAD,randomized exponentiation)几种，以从左至右的BR(LR-BR)算法为例，给出算法的操作步骤如下[12]。

设：

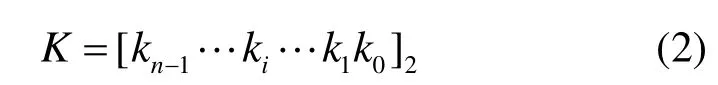
式中，n为K的二进制长度。

输入：P，K，N；

输出：C；

步骤：

1) 置初始值C=1；

2) 对于 i = n -1,… ,0 ，计算 C =C2(modN)；

3) 若 ki=1，计算 C = PC ( mod N )；

4) i ≠ 0 ，返回3)；

5) 输出结果。

BR算法在设计初，未考虑边信道信息泄露，因此极易受边信道攻击，文献[13] 分析了针对 BR算法各种可能的边信道攻击，并给出了真实环境下SPA攻击成功实例。

3 等功耗编码算法的分析与优化

针对BR算法中不同的操作导致功耗差异带来的边信息泄露而提出的等功耗编码实现算法[1]，其抗攻击基本原理是使每一次迭代循环的操作都相同，则每一次循环消耗的时间相等，消耗的能量差异也就难以区分。该实现算法无疑可以有效地抵抗计时和SPA攻击，也可使DPA攻击的难度大幅度增加。

3.1 幂剩余运算的等功耗编码算法原型

将式(1)中的指数K表示为

等功耗编码算法的步骤如下。

1) 预计算Rj余数表：

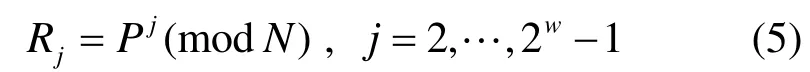
2) 置初始值C= 1；

3) 对于i=s - 1 ,… ,0 ，计算：

4) 若 ki= j≠ 0 ，计算： C= RjC(mod N)，否则，计算 aC( mod N)，其中a为常数；

5)i≠0 ，返回3)；

6) 输出结果C。

3.2 等功耗编码算法的改进与实现

3.2.1 等功耗编码原型算法的抗攻击弱点

在等功耗编码原型算法的第4）步中，当 ki=0时，只执行一个模乘运算；而在其值为非零时，要执行一个模乘运算，还执行一个赋值操作，这个微小的差别能被攻击者利用进行计时攻击，从而获取指数中的分段全零情况。

在不同的指数下， ki= 0 均使用相同常数 a进行冗余计算，其对功耗的影响是一致的，这个弱点也可被攻击者利用进行对比或模板分析攻击，获取指数中全零的情况。

3.2.2 等功耗编码算法的改进

针对 ki= 0 时算法的缺陷，提出以下改进方案。

ki= 0 时：

其中，U是一个辅助冗余变量，存储冗余计算的结果，消除 ki= 0 时无赋值运算操作的缺陷。而rand(R)为在余数表中随机抽取的一个余数，这样使得指数全0段对应的操作数与指数非全0段对应的操作数一样，从而在操作数上无法区分两者的差别，并且该随机函数的种子与指数K相关，保证在相同指数下获得相同的结果，这样可避免攻击者利用相同指数、明文反复运算，提取随机信息。

该改进方案增加了一个赋值操作，同时将原算法中常数 a改为随机余数值，使得 ki= 0 时操作与ki≠ 0 完全相同，且 ki= 0 时运算结果也与 ki≠ 0 一致，完全掩盖了 ki= 0 与 ki≠ 0 的差别，避免了针对ki= 0 的特殊攻击。

3.2.3 等功耗编码改进算法的快速实现

为提高算法的效率，采用蒙哥马利算法对改进算法中的模乘运算进行优化。

定义蒙哥马利算法模除M(T, N)为定义蒙哥马利算法模乘积MM(a, b, n)为

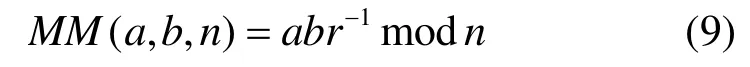
其中， r =2k, 2k-1≤ n ＜2k。

由式（9）可看出，蒙哥马利算法模乘积的结果并非原模乘积的结果，因此在使用蒙哥马利算法来实现等功耗编码算法时，需对原等功耗编码算法进行修正。

使用蒙哥马利算法的等功耗编码快速改进算法如下。

输入：P，K，N；

输出：C；

步骤：

1) 置初始值C=1 ；

2) 进行蒙哥马利运算预处理：

P ' =MM( P, r2mod N , N )= Prmod N

C ' =MM( C, r2mod N , N )= Crmod N

3) 预计算所有的 Rj，生成余数表：

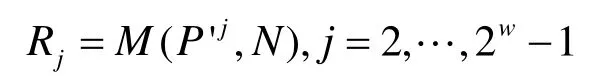
4) 对于 i = s - 1 ,… ,0 ，计算：

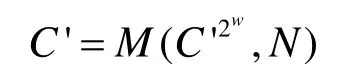
5) 若 xi= j≠ 0 ，计算：

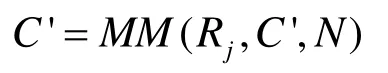
否则，计算 U=MM ( rand(R), C' N)；

6) i ≠ 0 ，返回4)；

7) 进行蒙哥马利运算后处理：

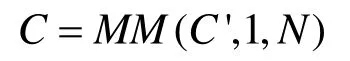
8) 输出结果C。

其中，rand（R）为在余数表中随机获取一个余数。

在该快速实现算法中，只有第2）步中r2modN为一般模乘运算，其余模乘运算均转换为蒙哥马利运算。与原算法相比，虽然增加了 2个预处理、1个后处理共3个蒙哥马利运算，但由于中间迭代次数较多，利用蒙哥马利运算替代一般模除运算的等功耗编码算法大大加快了整体算法的运算速度。

蒙哥马利算法针对不同的操作数，其运算是固定的，因此每次运算的能量消耗差异极小，一般的SPA攻击无法生效。

4 改进算法的抗攻击能力实测分析

4.1 真实硬件环境下的功耗分析模型

文献[13]对功耗分析模型与有效信息的提取技术进行了详细的讨论。本文使用了文献[13]中分析模型：

该模型可进行信号处理，提取有用信息，由于篇幅所限，具体的研究结果请参考文献[13]。

4.2 功耗测试平台

功耗模型和功耗分析需求设计和实现的测试平台框架如图 1所示。密码算法协处理单元使用Cyclone II 系列的EP2C8Q208C8 FPGA芯片为核心运算芯片，为做对比测试，片上先后实现了2组算法。

1) 数据总线宽度为 8bit的增加蒙哥马利预处理的幂剩余R-L算法（BR算法的一种），其中底数、指数、模数均为32bit。算法采用模平方与模乘并行运算结构，模平方与模乘均用蒙哥马利算法实现。

图1 测试平台框架

2) 数据总线宽度为 8bit的等功耗编码优化算法，其中底数、指数、模数均为32bit。w取值为2。

4.3 实测信号与指数相关性分析

4.3.1 R-L并行算法的功耗信号与分析

图2~图4为R-L并行算法在不同指数下经过信息处理后的幂剩余运算功耗轨迹图，各图像的不同之处正是对不同指数的刻画。经过对比观测可发现，各功耗轨迹图上均有界限分明的周期，正对应于幂剩余运算的轮迭代。

图2 指数为0x00000000时的功耗轨迹

图3 指数为0x12345678时的功耗轨迹

图4 指数为0xffffffff 时的功耗轨迹

从图3可以看出，功耗变化较大的位置正是2个模乘器同时工作时，对应指数取值为 1；功耗变化较小的位置对应指数取值为0。而在图2中，由于指数各比特位均相等，每次迭代所消耗功耗相同，因此各迭代间的波形几乎相同，图4的情况也是如此。由于对应指数0与1产生的功耗不同，从图2与图4对比可看出图4的功耗明显比图2大。

在图2~图4中，任意2个周期的时间间隔均相等，其原因是R-L并行算法消除了每次迭代的时间差异，因此无法在时间的差别上判断指数当前位的值，从而抵御了计时攻击。

需要指出的是，R-L并行算法需要2个模乘器同步工作，这在一般的单运算器上无法完成，因此算法应用有其局限性。

4.3.2 等功耗编码改进快速算法的功耗信号与抗攻击分析

在等功耗编码算法中，迭代的次数不是指数的比特数，具体的次数与w的取值相关。因此，在不知道w的情况下，无法通过计时直接确定指数的比特以及迭代起始位置。即使采用穷举搜索策略，计时攻击的难度也已增加。

由于在每轮迭代中，对应不同的指数，其运算操作完全相同，模平方运算和模乘运算均采用相同的蒙哥马利运算，仅是操作数有所不同，其运算时间均相同，攻击者无法通过每轮迭代的计时差异获取对应的指数信息。

从图5的波形上看，任意2个迭代内周期时间间隔均相等，波形一致，无法区分功耗的差别，可见改进后的快速等功耗编码实现算法达到了抗计时攻击的目的。

在改进的实现算法中，每一轮迭代循环（见步骤5））均要进行相同次数的蒙哥马利运算，其功耗情况在操作相关性上无法区分。

当指数ki为全零时，原算法只是采取了常数模乘运算，与其他指数情况下的操作存在一定差异。而在优化实现算法中，采用在余数表中随机选取一个余数进行蒙哥马利运算，并将该结果存入某存储单元，其操作与该余数对应指数运算时完全一致，直接混淆了全零与其他指数值运算时的功耗差别，比原始算法更具抗“指数段全0分析”SPA的性能，图5和图6分别是指数为0x12345678和0xffffffff时的等功耗编码改进快速算法功耗轨迹图，在SPA攻击者看来，两者之间没有差别，与图2和图4均相似。在采集大量的不同指数下该算法的功耗曲线进行分析后发现，各功耗曲线近似程度极大，无法从波形上进行SPA攻击得到指数取值信息。

针对等功耗编码算法的抗DPA特性[1]，DPA攻击主要利用运算的数据与功耗间的相关性进行攻击，可将系统噪声、静态伪操作形成的噪声通过差分剔除，原型算法中的静态伪操作实际可通过DPA鉴别出来。但对于优化后的实现算法，其伪操作与真实操作完全一致，无法用一般的DPA方法加以剔除，因此攻击者很难通过DPA直接区分“全0”和“非全0”指数段，实测结果限于篇幅，另撰文论述。

图5 指数为0x12345678时等功耗编码优化算法的功耗轨迹

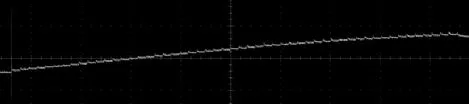
图6 指数为0xffffffff时等功耗编码优化算法的功耗轨迹

5 结束语

本文在讨论了等功耗编码算法的抗攻击弱点后，设计并实现了一个改进型快速等功耗编码算法。提高了算法的抗功耗分析性能。利用功耗分析平台，成功获取各算法实现的功耗轨迹图。通过对等功耗编码优化算法功耗轨迹图的分析，证实该算法确实能有效抵御计时和SPA攻击。该算法的抗DPA能力也在原理上被分析，其具体的实验验证另文论述。

致谢

作者诚挚感谢成都信息工程学院信息安全研究所的同仁万武南、索望、陈艾东、杜之波，研究生周俐莎、朱冰、刘鹤、饶金涛等，感谢他（她）们在课题研究中和论文撰写期间所做的大量协助工作和给予的无私帮助！没有他们的工作，也不会取得本文的研究成果。

[1] KOCHER P. Timing attacks on implementations of diffie-hellman,RSA, DES, and other systems[A]. Proceedings of Advances in Cryptology-CRYPTO’96[C]. 1996. 104-113

[2] DHEM J F, KOEUME F, LEROUX P A, et al. A practical implementation of the timing attack[A]. Proceedings of CARDIS 1998[C].1998.14-16.

[3] MESSERGES T S, DABBISH E A, SLOAN R H. Investigations of power analysis attacks on smartcards[A]. Proc USENIX Workshop Smartcard Technology[C]. Chicago, Illinois ,USA , 1999. 151-161.

[4] KOCHER P, JAFFE J, JUN B. Differential power analysis[A]. Proceedings of Advances in Cryptology-CRYPTO’99[C]. 1999. 388-397.

[5] ITOH K, IZU T, TAKENAKA M. Address-bit differential power analysis of cryptographic schemes OK-ECDH and OK-ECDSA[A]. CHES 2002[C]. 2003. 129-143.

[6] ITOH K, IZU T, TAKENAKA M. A practical countermeasure against address-bit differential power analysis C D[A]. CHES 2003[C].2003.382-396.

[7] CORSONELLO P. An integrated countermeasure against differential power analysis for secure smart-cards[A]. ISCAS[C]. 2006. 5611-5614.

[8] RATANPAL G B, WILLIAMS R D, BLALOCK T N. An on-chip signal suppression countermeasure to power analysis attacks[J]. IEEE Transactions on Dependable and Secure Computing, 2004, 1(3): 179-189.

[9] MESSERGES T S. Securing the AES finalists against power analysis attacks [A]. Proceedings of Fast Software Encryption Workshop 2000[C]. 2000.150-164.

[10] GEBOTYS C H. A table masking countermeasure for low-energy secure embedded systems[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2006, 14(7): 740-753.

[11] 陈运,吴震, 陈俊等. 防范边信道攻击的等功耗编码实现算法[J].电子科技大学学报, 2008,37 (2): 168-171.CHEN Y, WU Z, CHEN J, et al. Implementation of equivalent power consumption coding secure against side channel attack[J]. Journal of University of Electronic Science and Technology of China, 2008,37(2):168-171.

[12] 陈运. 信息加密原理[M]. 成都:电子科技大学出版社, 1996.CHEN Y. The Principle of Information Encryption[M]. University of Electronic Science and Technology of China Press, 1996.

[13] 吴震, 陈运, 陈俊等. 真实硬件环境下幂剩余功耗轨迹指数信息提取[J]. 通信学报, 2010, 31(2): 17-21.WU Z, CHEN Y, CHEN J, et al. Exponential information’s extraction from power traces of modulo exponentiation implemented on FPGA[J].Journal on Communications, 2010,31(2): 17-21.