无线传感器网络中的分布式Voronoi覆盖控制算法

徐鹏飞，陈志刚，邓晓衡

(1. 中南大学 信息科学与工程学院，湖南 长沙 410083；2. 湖南师范大学 数学与计算机科学学院，湖南 长沙 410081)

1 引言

传感器网络是由部署在目标区域内的大量廉价、微型传感器节点，通过自组织构成一个无中心控制、无基础设施的无线网络系统，广泛运用于军事、环境监测等领域[1]；传感器节点通过能量有限的电池供电，节能成为传感器网络的重要研究内容[1,2]。覆盖控制是选择部分节点活跃工作(即活跃节点)，将其余节点(即冗余节点)转入能耗较低的睡眠状态，是一种提高网络能量效率、延长网络生存时间的有效策略[2,3]。

为了保证传感器网络的感知、通信等服务质量，活跃节点应维持网络原有覆盖范围与连通性，综合考虑节点能量、控制方式等因素[3]。在传感器网络覆盖部分目标区域的假设条件下，本文提出一种维持网络原有覆盖范围、连通性的分布式Voronoi覆盖控制算法(DVC, distributed voronoi coverage algorithm)。仿真实验表明，DVC活跃节点的数量与覆盖度接近集中式算法，优于一般的分布式算法；而活跃节点的平均能量和算法性能更加具有优势。

本文组织如下：第2节介绍相关研究工作；第3节定义网络覆盖模型；第4节详细描述算法与有关结论；第5节为仿真实验；第6节是结束语。

2 相关研究

分布式覆盖控制包括冗余识别与冗余调度2个基本问题[4]；其中冗余识别判断节点是否为冗余节点，冗余调度确定将哪些冗余节点转入睡眠状态。文献[4]使用扇区并集近似描述节点间重叠的覆盖范围，提出随机时间退避的冗余调度规则。文献[5]将节点覆盖范围划分为虚拟网格，每个网格至少被一个邻居覆盖时为冗余节点，提出令牌驱动的冗余调度规则。文献[6]将节点覆盖范围简化为覆盖圆盘的边界，提出圆周覆盖的概念。文献[7]通过实例说明圆周覆盖可能将节点误识为冗余节点，提出相应规则降低误识率，运用支配集进行冗余调度。上述文献只能近似维持网络原有覆盖范围，冗余识别复杂度、冗余调度收敛性与节点密度相关，目标区域边界附近的活跃节点过多。

实际上，每个节点原则上只要覆盖目标区域内与自己最近的点，为此国内外学者提出使用计算几何的Voronoi划分研究冗余识别[8～11]。文献[8]使用Voronoi区域的面积阈值识别冗余节点，很难有效维持网络原有覆盖范围。文献[9]通过重构剔除节点后的 Voronoi划分来识别冗余节点，计算复杂度为O(n2lgn)；文献[8]与文献[9]通过集中方式实现。文献[10]与文献[11]基于Voronoi划分的冗余识别规则相对比较简单，可以使用随机时间退避、支配集等方式进行分布式冗余调度。但是上述基于Voronoi划分的冗余识别要求网络覆盖整个目标区域；事实上，随机部署网络覆盖整个目标区域时将导致高冗余度[12]，节点能量耗尽也可能导致网络不能覆盖整个目标区域[13]。

本文主要工作：1) 在网络覆盖部分目标区域的假设条件下，提出一种基于局部Voronoi区域的冗余识别规则，其计算复杂度与节点密度无关，完善已有的Voronoi覆盖理论；2) 提出一种能量优先的Voronoi调度规则，通信相邻、局部Voronoi不相邻的节点可以同步执行冗余识别，提高分布式调度的收敛性。3) 通过仿真实验，分析随机均匀部署网络的覆盖质量以及本文算法的有效性。

3 问题描述

定义1（假设条件） 给定目标区域R2内n(≥3)个互不重叠的传感器节点集S。

1) 假设节点具有相同传感半径 Rs，节点 u∈S的覆盖范围是以节点u为圆心、Rs为半径的圆盘，记为覆盖圆Cu；当且仅当点p∈R2满足||up||≤Rs(即p∈Cu)时，节点u覆盖点p或点p被节点u覆盖；其中||·||表示2个点之间的欧氏距离。

2) 如果存在点 p∈R2与任意节点 u∈S满足||up||＞Rs，则传感器节点集S仅覆盖部分目标区域，即部分覆盖网络；否则，传感器节点集S可以覆盖整个目标区域，即完全覆盖网络。在部分覆盖网络中，不能被任意节点覆盖的点简称覆盖盲点，覆盖盲点的集合简称覆盖盲区。

3) 将目标区域 R2简化为整个平面，任意覆盖圆在目标区域R2内，所有覆盖圆的并集构成网络的原有覆盖范围C；本文研究部分覆盖网络下的覆盖控制，这种简化不影响问题的分析，即将目标区域R2内除覆盖范围 C外的子区域作为网络的覆盖盲区；若无特别说明，本文区域R2是指整个平面。

4) 假设节点具有相同通信半径Rc，且Rc≥2Rs（注意，本文的实例分析假设Rc=2Rs。）；相互位于通信半径范围的节点互为通信邻居或通信相邻。

定义 2（Voronoi划分[14]） 给定平面 R2内 n(≥3)个互不重叠的节点集S。

1) 点p∈R2与节点集S中的节点u最近，当且仅当点 p 与任意节点 x∈S(x≠u)满足||up||≤||px||。

2) 平面R2内所有与节点u∈S最近点的集合构成节点u的Voronoi区域V(R2,S,u)，

3) 节点u、x∈S之间的垂直平分线记为L(u,x)，以垂直平分线L(u,x)为界、包含节点u的半平面记为H(u,x)；任意点p∈R2，当且仅当满足||up||≤||px||与 u≠x时有 p∈H(u,x)，则

4) 将平面R2内每个点划分到节点集S中最近的节点，即所有Voronoi区域的并集，构成节点集S在平面R2内唯一的Voronoi划分V(R2,S)。

定义 3（Voronoi覆盖） 对目标区域 R2内的传感器节点集S求解Voronoi划分V(R2,S)。

1) 当且仅当任意点 p∈V(R2,S,u)满足||up||≤Rs时，V(R2,S,u)或节点u满足Voronoi覆盖；换言之，V(R2,S,u)满足 Voronoi覆盖，当且仅当节点u∈S覆盖目标区域R2内所有与自己最近的点。

2) 当且仅当节点集S中每个节点满足Voronoi覆盖时，V(R2,S)满足Voronoi覆盖；换言之，V(R2,S)满足Voronoi覆盖，当且仅当目标区域R2内任意点被节点集S中的最近节点覆盖。

定义 4（局部 Voronoi覆盖） 给定目标区域R2内的传感器节点集S与传感半径Rs。

1) 设节点u∈S与其2Rs范围内的邻居为N(u)，则V(R2,N(u),u)为节点u的局部Voronoi区域。

2) 当且仅当任意点 p∈V(R2,N(u),u)满足||up||≤Rs(即 V(R2,N(u),u)位于覆盖圆 Cu内)时，V(R2,N(u),u)或节点u满足局部Voronoi覆盖。

例如，图 1(a)给出节点集 S={u1,…,u12}的Voronoi划分 V(R2,S)，图 1(b)给出每个节点的局部Voronoi区域，其中实线围成包含一个节点的凸区域即为该节点的(局部)Voronoi区域。

定义 5（Voronoi性质[14]） 给定 Voronoi划分V(R2,S)。

1) Voronoi区域的边界简称 Voronoi边；如果V(R2,S,u)与V(R2,S,k)存在公共的Voronoi边，则节点u、k∈S(u≠k)共享 Voronoi边或互为 Voronoi邻居（即Voronoi相邻）。

2) 节点u∈S满足u∈V(R2,S,u)、且不在Voronoi边上；任意节点 k∈S(u≠k)满足 k∉V(R2,S,u)。

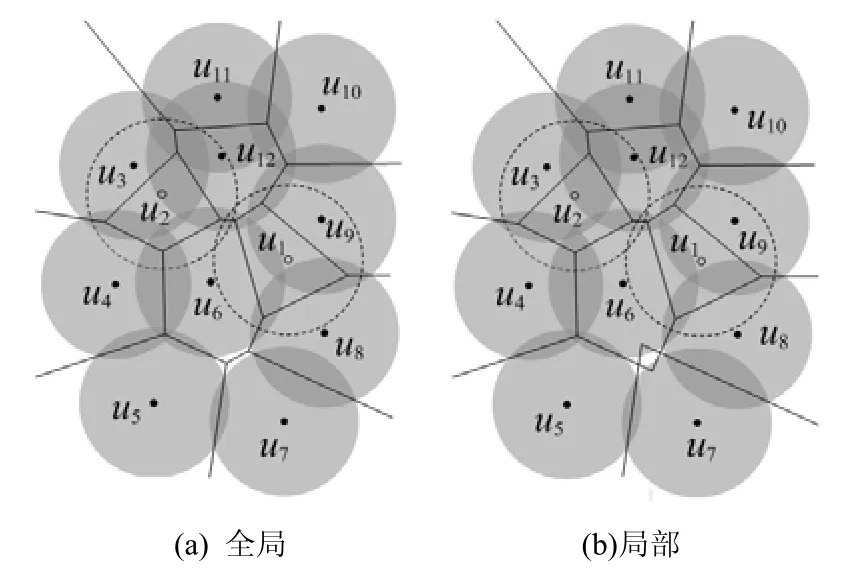
图1 Voronoi划分与Voronoi覆盖

3) 如果点p∈V(R2,S,u)不在Voronoi边上，则任意节点 k∈S(k≠u)满足||kp||＞||pu||。

4) 设节点u的所有Voronoi邻居为Vn(R2,S,u)，当且仅当 k∈Vn(R2,S,u)时有 u∈Vn(R2,S,k)。

5) 当且仅当 V(R2,S,u)∩L(u,k)≠φ，节点 u、k∈S(u≠k)共享 Voronoi边(V(R2,S,u)∩L(u,k))。

6) Voronoi区域是由Voronoi边围成的凸多边形区域，即

定义6 给定局部Voronoi区域V(R2,N(u),u)与局部Voronoi邻居Vn(R2,N(u),u)，将区域V(R2,N(u),u)内每个点划分到节点集 Vn(R2,N(u),u)中，最近节点后的Voronoi划分为V(V(R2,N(u),u),Vn(R2,N(u),u))。

定义7（冗余） 当且仅当任意点p∈Cu存在节点k∈(S-u)满足||kp||≤Rs时，节点u为冗余节点或节点u满足冗余[9]；换言之，节点u满足冗余，当且仅当任意点p∈Cu被节点集S-u中最近的节点覆盖。

4 部分覆盖网络下的分布式Voronoi覆盖控制

4.1 基于局部Voronoi区域的冗余识别规则

当网络覆盖部分目标区域时，任意节点根据其2Rs范围的邻居求解局部Voronoi区域后，至少有一个节点不满足局部Voronoi覆盖[15]。

4.1.1 节点不满足局部Voronoi覆盖

通过分析Voronoi区域V(R2,S,u)与局部Voronoi区域V(R2,N(u),u)的关系，然后给出节点u在不满足局部Voronoi覆盖时的冗余识别规则。

引理 1 任意Voronoi区域V(R2,S,u)与局部Voronoi区域 V(R2,N(u),u)满足 V(R2,S,u)⊆V(R2,N(u),u)[15]。

证明 依据式(2)将V(R2,S,u)改写为

依据式(2)有 V(R2,N(u),u)=∩x∈(N(u)-u)H(u,x)，将其代入式(3)后有

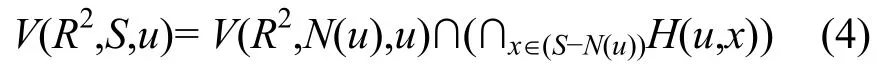
式(4)表明 V(R2,S,u)⊆V(R2,N(u),u)。证毕。

推论 1 如果 V(R2,N(u),u)不满足局部 Voronoi覆盖，则V(R2,S,u)不满足Voronoi覆盖。

证明 依据引理 1，V(R2,S,u)与 V(R2,N(u),u)满足下列情况之一。1) V(R2,S,u)=V(R2,N(u),u)：则V(R2,S,u)不满足Voronoi覆盖；2) V(R2,S,u)⊂ V(R2,N(u),u)：V(R2,S,u)位于区域 V(R2,N(u),u)内，V(R2,S,u)至少有一条 Voronoi边 e与V(R2,N(u),u)的任意Voronoi边不重叠(否则，将有 V(R2,S,u)=V(R2,N(u),u))，依据Voronoi性质 5)设 e=V(R2,S,u)∩L(u,k)，则 e≠φ；设V(R2,N(u),u)∩L(u,k)=λ，已知V(R2,S,u)⊂V(R2,N(u),u)，则有 e⊂λ与λ≠φ；如果 k∈N(u)，V(R2,N(u),u)依据Voronoi性质5)将有Voronoi边λ，这样Voronoi边e与V(R2,N(u),u)的Voronoi边λ重叠，与假设“Voronoi边e与V(R2,N(u),u)的任意Voronoi边不重叠”矛盾，即 只 能 有 k∉N(u)与||uk||＞2Rs； 点 p∈e 满 足p∈V(R2,S,u)、p∈L(u,k)，垂直平分线 L(u,k)上的点 p满足||up||≥||uk||/2＞Rs，即存在点 p∈V(R2,S,u)满足||up||＞Rs，V(R2,S,u)不满足 Voronoi覆盖。综合上述，当 V(R2,N(u),u)不满足局部 Voronoi覆盖时，必有V(R2,S,u)不满足Voronoi覆盖。证毕。

推论2 如果V(R2,S,u)不满足Voronoi覆盖，则节点u必定不满足冗余。

证明 V(R2,S,u)不满足 Voronoi覆盖时，将存在点q∈V(R2,S,u)满足q∉Cu；节点u为覆盖圆Cu的圆心，线段uq与覆盖圆Cu的边界交于一点p，则有||pu||=Rs(即 p∈Cu)与 p∈uq(p≠q, p≠u)；依据 Voronoi性质2)，节点u∈V(R2,S,u)不在Voronoi边上，则线段uq在区域V(R2,S,u)内、与V(R2,S,u)的任意Voronoi边不重叠，也就是点p∈V(R2,S,u)不在Voronoi边上；依据 Voronoi性质 3)，任意节点 k∈S(k≠u)满足||kp||＞||pu||与||kp||＞Rs。综合上述，V(R2,S,u)不满足 Voronoi覆盖时，存在点 p∈Cu与任意节点 k∈(S-u)满足||kp||＞Rs，节点u不满足冗余。证毕。

定理 1 如果 V(R2,N(u),u)不满足局部 Voronoi覆盖，则节点u必定不满足冗余。

证明 依据推论1与推论2可知。

4.1.2 节点满足局部Voronoi覆盖

当V(R2,N(u),u)满足局部Voronoi覆盖时，区域V(R2,N(u),u)位于覆盖圆Cu内，覆盖圆Cu划分为不相交的子集：V(R2,N(u),u)与Cu-V(R2,N(u),u)；依据定义7，当且仅当这2个区域内任意点都能被节点集S-u中最近的节点覆盖时，节点u满足冗余。

推论 3 任意点 q∈(Cu-V(R2,N(u),u))存在节点m∈S(m≠u)满足||mq||≤Rs与 q∈V(R2,N(m),m)。

证明 已知 q∉V(R2,N(u),u)与 q∈Cu，则有||uq||≤Rs与 q∈R2；若 q∈R2，依据式(1)存在节点 m∈S满足q∈V(R2,S,m)；若q∉V(R2,N(u),u)，依据引理1有q∉V(R2,S,u)，则有 m≠u；若 q∈V(R2,S,m)，依据式(1)有||mq||≤||uq||，则有||mq||≤Rs；依据引理 1有 V(R2,S,m)⊆V(R2,N(m),m)，则有 q∈V(R2,N(m),m)。证毕。

推论4 如果V(R2,N(u),u)满足局部Voronoi覆盖，则V(R2,S,u)=V(R2,N(u),u)、Vn(R2,S,u)=Vn(R2, N(u), u)。

证明 V(R2,N(u),u)满足Voronoi覆盖时，任意点 p∈V(R2,N(u),u)满 足 ||up||≤ Rs； 任 意 节 点x∈(S-N(u))满足 u≠x 与||ux||＞2Rs，也就有||up||＜||ux||/2与 p∈H(u,x)，则有 p∈(∩x∈(S-N(u))H(u,x))；综合上述，有 V(R2,N(u),u)⊆(∩x∈(S-N(u))H(u,x))，依据式(4)有V(R2,S,u)=V(R2,N(u),u)，根据Voronoi邻居定义又有Vn(R2,S,u)=Vn(R2,N(u),u)。证毕。

引理2 如果点p∈V(R2,S,u)与节点集Vn(R2,S,u)中最近的节点为k，则点p与节点集S-u中最近的节点仍是k。

证明 详细见文献[11]的引理5.3证明。

推论5 当V(R2,N(u),u)满足局部Voronoi覆盖时，如果任意点 p∈V(R2,N(u),u)被节点集Vn(R2,N(u),u)中最近的节点覆盖，则节点 u满足冗余；否则，节点u不满足冗余。

证明 依据推论3，区域(Cu-V(R2,N(u),u))内任意点必被节点集S-u中最近的节点覆盖，节点u是否冗余取决于，区域V(R2,N(u),u)内任意点是否被节点集S-u中最近的节点覆盖；设点p∈V(R2,N(u),u)与节点集 Vn(R2,N(u),u)中最近的节点为 k。已知V(R2,N(u),u)满足 Voronoi覆盖，依据推论 4有V(R2,S,u)=V(R2,N(u),u)与 Vn(R2,S,u)=Vn(R2,N(u),u)，则点 p∈V(R2,S,u)与节点集 Vn(R2,S,u)中最近的节点为k；依据引理2，点p与节点集S-u中最近的节点为 k；换言之，任意点 p∈V(R2,N(u),u)被节点集Vn(R2,N(u),u)中最近的节点k覆盖，点p必被节点集S-u中最近的节点k覆盖，节点u满足冗余；否则，存在点 p∈V(R2,N(u),u)不能被节点集 Vn(R2,N(u),u)中最近的节点k覆盖，点p也不能被节点集S-u中最近的节点k覆盖，节点u不满足冗余。证毕。

定理 2（Voronoi冗余） 当 V(R2,N(u),u)满足Voronoi覆盖时，如果V(V(R2,N(u),u)、Vn(R2,N(u),u))满足Voronoi覆盖，则节点u满足冗余，简称Voronoi冗余；否则，节点u不满足冗余。

证明 如果 V(V(R2,N(u),u)、Vn(R2,N(u),u))满足Voronoi覆盖，则任意点 p∈V(R2,N(u),u)被节点集Vn(R2,N(u),u)中最近的节点覆盖，依据推论5有节点u满足冗余；否则，存在点p∈V(R2,N(u),u)不能被节点集 Vn(R2,N(u),u)中最近的节点覆盖，依据推论 5将有节点u不满足冗余。证毕。

定理 2与文献[11]的区别是，任意满足局部Voronoi覆盖的节点可以进行Voronoi冗余识别，不管其他节点是否满足局部 Voronoi覆盖，即定理 2允许网络覆盖部分目标区域；文献[11]要求网络覆盖整个目标区域，此时所有节点满足局部 Voronoi覆盖[15]；因此，文献[9]与文献[11]是定理2的特例情况，定理1与定理2将进一步完善文献[9]与文献[11]的Voronoi覆盖理论。

例如图 1(b)，节点 ui(i=3,…,11)不满足局部Voronoi覆盖，节点u1、u2满足局部Voronoi覆盖，依据定理2可知节点u1、u2满足Voronoi冗余，如图2(a)所示；从图1可以发现节点u1、u2确实为冗余节点。

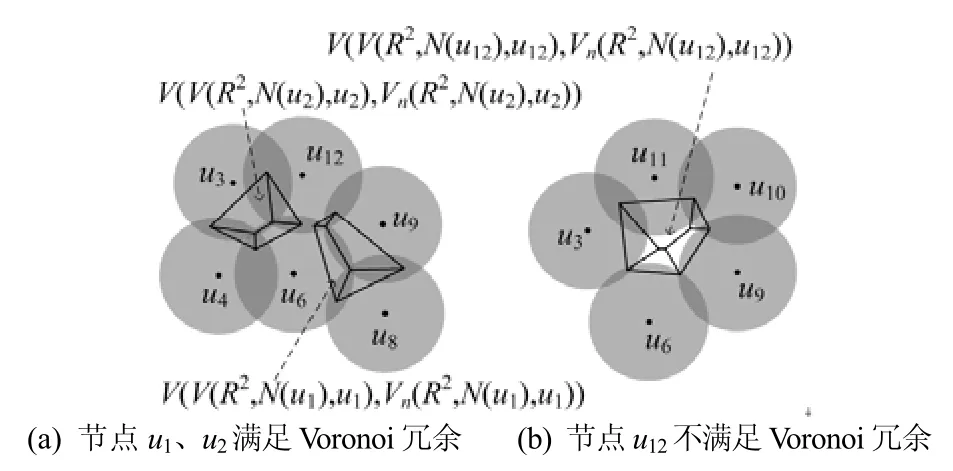
图2 Voronoi冗余实例

4.2 能量优先的Voronoi调度规则

任意节点根据2Rs范围的邻居，定理 1与定理2可以独自确定是否冗余。为了维持网络原有覆盖范围，不满足冗余的节点只能为活跃(Active)状态，不能转入睡眠(Sleep)状态[9]；一个冗余节点能否转入 Sleep状态，应根据其他节点的状态来确定。为此，本文提出一种能量优先的Voronoi调度策略。

4.2.1 调度算法描述

假设节点通过消息交互维护2Rs范围内的邻居位置、能量与状态等信息。首先，将N(u)中所有节点标记为Unset状态；然后，节点u通过调度策略确定最终状态(Active或Sleep)后，向N(u)中所有邻居广播最终状态消息；最后，如果节点u为Active状态，则继续接收邻居的状态消息，直到N(u)中所有邻居确定最终状态，以维护活跃邻居信息。

其调度策略如下：1) V(R2,N(u),u)不满足局部Voronoi覆盖：节点u依据定理1将不满足冗余，设置为Active状态。2) V(R2,N(u),u)满足局部Voronoi覆盖：节点u先接收N(u)中邻居的状态消息，标记N(u)中的Active节点、剔除N(u)中的Sleep节点；当Vn(R2,N(u),u)中包含Sleep节点时，重构剔除Sleep节点后的V(R2,N(u),u)；当Vn(R2,N(u),u)中所有能量较低(若能量相同，则节点 ID 值较小)节点确定为Active状态后，节点u使用定理2进行冗余识别；如果节点u满足Voronoi冗余，则为Sleep状态；否则为Active状态。

其算法详细步骤如图3所示，节点的任务/状态转换如图4所示(注意：为了简化问题描述，下文假设任意2个节点的能量不同)。

图3 DVC算法

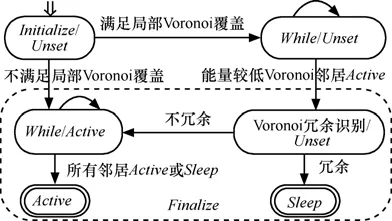
图4 调度的任务/状态转换

4.2.2 调度实例分析

1) 设图1(b)所示网络的目标区域为整个平面，节点能量为其编号。初始化时，不满足局部Voronoi覆盖的节点ui(i=3,…,11)设置为Active状态，满足局部Voronoi覆盖的节点u1、u2、u12进入While/Unset循环；第1轮，节点u1、u2退出While/Unset循环，执行 Voronoi冗余识别后为 Sleep状态，如图 2(a)所示；第2轮，节点u12收到节点u1、u2的睡眠消息，重构局部Voronoi区域、退出While/Unset循环，执行Voronoi冗余识别后为Active状态，如图2(b)所示。每轮调度的节点状态变化如表1所示。

表1 DVC调度实例

2) 如果目标区域为整个平面，则不满足局部Voronoi覆盖的节点称为边界节点[15]；当目标区域为有界区域时，应将有界目标区域与节点的局部Voronoi区域进行交集操作[9]，这样一些边界节点有可能满足局部Voronoi冗余。例如图5 (a)所示，目标区域为整个平面时，边界节点u1、u2、u3不是冗余节点；如果目标区域的边界为图5(a)的实线方框，则节点u1满足Voronoi冗余，如图5(b)所示。

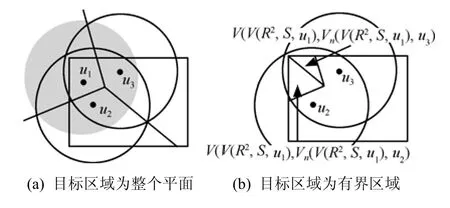
图5 有界目标区域调度实例

4.2.3 算法正确性分析

结论 1 通信相邻、局部 Voronoi不相邻的节点可以同步执行Voronoi冗余识别。

证明 设V(R2,N(u),u)满足局部Voronoi覆盖，任意局部 Voronoi邻居 k∈Vn(R2,N(u),u)满足k∈Vn(R2,S,u)(推论 4)，则有 u∈Vn(R2,S,k)(Voronoi性质4))；节点u执行Voronoi冗余识别时，V(R2,N(k),k)有下列情况之一。

1) 不满足局部Voronoi覆盖：节点k在初始化时已经设置为Active状态。

2) 满足局部 Voronoi覆盖：依据推论 4有Vn(R2,N(k),k)=Vn(R2,S,k)，则有 u∈Vn(R2,N(k),k)；若k.E＞u.E，节点k至少要收到节点u的状态消息后执行Voronoi冗余识别，即节点k处于While/Unset循环；否则，节点 u至少要收到节点 k的状态消息后执行Voronoi冗余识别，即节点k为Active状态(若为Sleep状态，则已从 N(u)剔除了节点 k，有 k∉Vn(R2,N(u),u))。

综合上述，节点u执行Voronoi冗余识别时，其任意局部Voronoi邻居k或处于While/Unset循环或为Active状态，不会转入睡眠状态；换言之，局部Voronoi相邻节点异步执行Voronoi冗余识别，局部Voronoi邻居为通信邻居的子集，即通信相邻、局部 Voronoi不相邻的节点可以同步执行 Voronoi冗余识别。证毕。

例如，根据图1(b)可知节点u1、u2满足通信相邻、局部 Voronoi不相邻；根据表 1，节点 u1、u2同步执行Voronoi冗余识别后转入睡眠状态。

推论6 如果V(R2,N(u),u)满足局部Voronoi覆盖，点p∈V(R2,N(u),u)与节点集Vn(R2,N(u),u)中最近的节点为k，则有p∈V(R2,(N(k)-u),k)。

证明 依据推论5的证明，点p与节点集S-u中最近的节点仍是k，依据式(1)有p∈V(R2,(S-u),k)；显然，(N(k)-u)为(S-u)的子集，依据引理 1有V(R2,(S-u),k)⊆V(R2,(N(k)-u),k)，则有 p∈V(R2,(N(k)-u),k)。证毕。

结论2 DVC可以维持网络原有的覆盖范围。

证明 设V(R2,N(u),u)满足局部Voronoi覆盖，节点u执行Voronoi冗余识别后转入睡眠状态。

1) 任意点 p∈V(R2,N(u),u)：节点集 Vn(R2,N(u),u)中与点p最近的节点k可以覆盖点p(推论5)。若节点k为活跃状态，则节点k在任何时刻都可以覆盖点p；否则，处于While/Unset循环的节点k(结论1的证明)在收到节点u的睡眠消息后，重构剔除节点u后的局部Voronoi区域将包含点p(推论6)；节点k在后继调度过程中，只有其局部Voronoi邻居覆盖点p的情况下，才有可能转入睡眠状态。

2) 任意点 q∈(Cu-V(R2,N(u),u))：存在节点 m∈S(m≠u)满足 q∈V(R2,N(m),m)与||mq||≤Rs(推论 3)；若节点m为活跃状态，节点m在任何时刻都可以覆盖点q；否则，将有V(R2,N(m),m)满足局部Voronoi覆盖，节点m只有在其局部Voronoi邻居覆盖点q∈V(R2,N(m),m)的情况下，才有可能转入睡眠状态。

综上所述，Voronoi冗余节点转入睡眠状态后，其覆盖圆内任意点可以被其他节点覆盖，不会转变为覆盖盲点，即可以维持网络原有覆盖范围。证毕。

推论 7 如果 Rc≥2Rs、V(R2,S)满足 Voronoi覆盖，则节点集S构成连通网络。

证明 V(R2,S)的直线对偶图D(S)为连通图，图D(S)中任意边关联的节点u、k共享Voronoi边e[14]；依据 Voronoi性质 5)设 e=V(R2,S,u)∩L(u,k)，点p∈e满足 p∈V(R2,S,u)、p∈L(u,k)；若 V(R2,S)满足 Voronoi覆盖，有 V(R2,S,u)满足 Voronoi覆盖，则有||up||≤Rs；垂直平分线 L(u,k)上的点 p满足||uk||≤2||up||，则有||uk||≤Rc；因此，连通图 D(S)的任意边即为一条通信链路，节点集S构成连通网络。证毕。

推论 8 任意节点 u、k∈S(k≠u)存在节点 m∈Vn(R2, S,u) (m≠u)满足||km||＜||ku||。

证明 根据 Voronoi性质 2)有 k∉V(R2,S,u)；设k=p，则有p∉V(R2,S,u)；如果任意节点x∈Vn(R2,S,u)满足 p∈H(u,x)，根据 Voronoi性质 6)有 p∈V(R2,S,u)，与“p∉V(R2,S,u)”矛盾；即存在节点m∈Vn(R2,S,u)满足m≠u与 p∉H(u,m)，则有||up||＞||pm||，即||km||＜||ku||。证毕。

结论3 如果Rc≥2Rs，则DVC可以保持网络原有连通性。

证明 设V(R2,N(u),u)满足局部Voronoi覆盖，节点u执行Voronoi冗余识别后转入睡眠状态；依据定理 2有 V(V(R2,N(u),u),Vn(R2,N(u),u),u)满足Voronoi覆盖，不会转入睡眠状态的节点集Vn(R2,N(u),u)(结论1的证明)构成连通子网(推论7)；节点 u的任意通信邻居 k(即||ku||≤Rc)存在节点m∈Vn(R2,S,u)满足||km||＜||ku||与||km||≤Rc(推论 8)；根据推论5有Vn(R2,S,u)=Vn(R2,N(u),u)；综上所述，节点 u的任意 2个通信邻居可以通过节点集Vn(R2,N(u),u)连通，即Voronoi冗余节点转入睡眠状态后不影响网络原有连通性。证毕。

引理3 给定n个节点，求解任意Voronoi区域的计算复杂度为O(n)[15]。

结论 4 Voronoi冗余识别的计算复杂度为O(1)，与节点密度无关。

证明 Voronoi边的交点简称Voronoi顶点，节点满足Voronoi覆盖等价于其所有Voronoi顶点在覆盖圆内[9,11,15]；V(R2,N(u),u)的局部Voronoi邻居与局部Voronoi顶点的平均值为 6，与节点数量无关[14]。分别求解 V(R2,N(u),u)满足局部 Voronoi覆盖与V(V(R2,N(u),u),Vn(R2,N(u),u))满足 Voronoi覆盖的计算复杂度均为 O(1)。综合上述，Voronoi冗余识别的计算复杂度为O(1)，与节点密度无关。证毕。

结论5 DVC的计算复杂度为O(m2)，其中m为2Rs范围内的邻居数。

证明 根据引理3，初始化求解Vn(R2,N(u),u)、While/Unset循环重构 V(R2,N(u),u)的计算复杂度均为O(m)；Vn(R2,N(u),u)中能量较低节点确定为Active状态后退出While/Unset循环，Vn(R2,N(u),u)为N(u)的子集，循环次数不会超过m，即While/Unset循环的计算复杂度为O(m2)；Finalize过程中Voronoi冗余识别的计算复杂度为 O(1)。综上所述，DVC的计算复杂度为O(m2)。

结论6 DVC的消息复杂度为O(1)，整个网络的消息复杂度为O(n)，其中n为网络节点数。

证明 每个节点初始化时通过 1个消息维护2Rs范围内的邻居信息，确定最终状态后向2Rs范围内的邻居广播1个状态消息；即DVC的消息复杂度为O(1)，整个网络的消息复杂度为O(n)。证毕。

5 仿真实验分析

本文利用 C++进行算法实现与仿真，与 CVT算法[9]、ECC算法[7]进行比较。实验环境为 P4 2.4GHz CPU与512MB内存；实验场景如下：在目标区域1 000×1 000内随机均匀部署n个互不重叠的节点，分析节点数量n(即部署密度)、传感半径Rs(设Rc=2Rs)对活跃节点与算法性能的影响；其中每个n值随机产生500个网络拓扑，每个网络拓扑随机分配50个能量方案(节点能量≤10)。

5.1 随机均匀部署网络的覆盖质量

为了分析随机均匀部署网络的覆盖质量，统计500个网络拓扑中完全覆盖网络的比率(PCC)、覆盖目标区域的面积比率(RCT)以及网络覆盖度；当PCC、RCT小于100%时，网络覆盖部分目标区域。

1) 随机均匀部署500～2 000个节点后：① 当Rs=50时，不能保证每个网络拓扑覆盖整个目标区域，但是网络覆盖目标区域的面积比率RCT已经超过 97%，覆盖盲区的面积不到 3%；特别是n＜1 000时，完全覆盖网络的比率PCC接近0，如图 6(a)所示；② 当 Rs=100时，网络覆盖目标区域的面积比率RCT已经超过99%；直到n＞1 000，完全覆盖网络的比率 PCC才收敛于 100%；如图6(b)所示。

图6 覆盖质量分析

2) 随机均匀部署n个节点，随着传感半径Rs的增大，覆盖整个目标区域的概率增大。当n=1 000、Rs≥100时，完全覆盖网络的比率PCC收敛于 100%，如图 6(c)所示；当 n=1 500、Rs≥80时，完全覆盖网络的比率PCC收敛于100%，如图6(d)所示；当n≥1 000、Rs≥50时，网络覆盖目标区域的面积比率RCT已经超过99.8%。

3) 设覆盖点 p∈R2的节点数为 K(p)，覆盖度是衡量网络能量效率、覆盖冗余程度的一个指标[9]。随机均匀部署网络的覆盖度，随着节点数量n近似线性增长，随着传感半径Rs近似指数增长，如图7所示；当网络覆盖目标区域的面积比率RCT接近99.99%时，覆盖度大约为13，如图7的圆圈所示；当网络覆盖整个目标区域时，覆盖度已经达到30以上，如图7的方框所示。

图7 网络平均覆盖度

5.2 活跃节点的数量

当Rs=50时，DVC活跃节点将随着节点数量n近似收敛于282，如图8(a)所示；当Rs=100时，DVC活跃节点将随着节点数量 n近似收敛于 75，如图8(b)所示；随机均匀部署 n个节点后，随着传感半径Rs的增大，DVC活跃节点将逐渐减少，如Rs=200时的活跃节点大约减至 20个，如图 8(c)、图 8(d)所示。综合上述实验数据发现，DVC活跃节点数量基本上与部署密度无关，主要由传感半径Rs确定；总的来说，随着节点数量n或传感半径Rs的增大，DVC活跃节点相对减少，冗余节点相对增多。

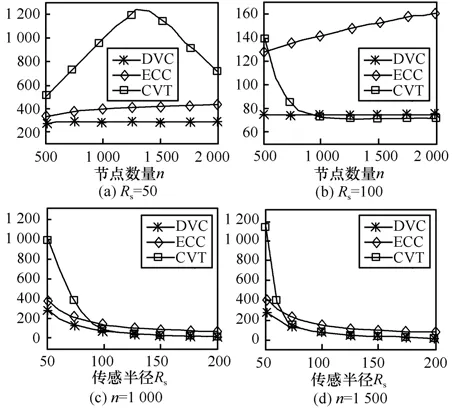
图8 活跃节点的数量

ECC算法不考虑目标区域边界，简单地将所有边界节点设置为活跃状态，使得ECC活跃节点大约维持在DVC的1.1～3.5倍；因此，合理使用目标区域的边界可以有效地降低边界附近的活跃节点。网络覆盖整个目标区域时，CVT活跃节点稍微优于DVC，其差值不超过DVC活跃节点的4.5%；网络覆盖部分目标区域时，尽管存在冗余节点，但是CVT将所有节点设置为活跃状态，使得CVT活跃节点大于DVC与ECC。

5.3 睡眠节点的比率

初始网络节点中睡眠节点的比率(RoS)如图 9所示，DVC将 40%以上的节点转入睡眠状态；当RCT收敛到99%时，DVC将60%的节点转入睡眠状态，如图9的方框所示；当RCT收敛到99.99%时，DVC将 80%的节点转入到睡眠状态，如图 9的圆圈所示。总的来说，随机均匀部署网络覆盖部分目标区域时，在维持原有覆盖质量的前提下，仍存在大量的冗余节点，因此研究部分覆盖网络环境下的Voronoi覆盖控制具有重要的意义。

5.4 活跃节点的平均覆盖度

活跃节点的平均覆盖度与节点数量n、传感半径Rs的关系如图10所示。DVC活跃节点的平均覆盖度大约维持在2.5，基本上与节点数量n、传感半径Rs无关。网络覆盖整个目标区域时，CVT活跃节点的平均覆盖度稍微优于 DVC，其差值小于 0.1；网络覆盖部分目标区域时，CVT活跃节点的平均覆盖度明显大于DVC。ECC将边界节点设置为活跃状态，随着节点数量n或传感半径Rs的增大，ECC活跃节点的平均覆盖度呈上扬趋势，大于DVC。

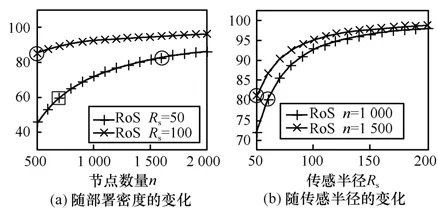
图9 睡眠节点的比率

图10 活跃节点的平均覆盖度

5.5 活跃节点的平均能量

设DVC活跃节点数量为x，选择x个能量最大节点的平均值作为活跃节点的最佳能量；图 11给出实验场景Rs=100与n=1 000中活跃节点的平均能量、最佳能量以及初始网络的节点平均能量。

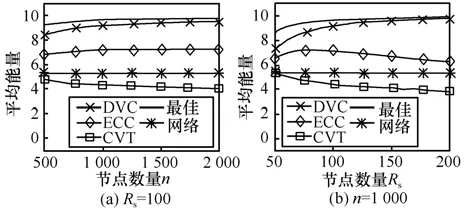
图11 活跃节点的平均能量

随着节点数量n或传感半径Rs的增大，DVC活跃节点相对减少，使得最佳能量逐渐增大；DVC将能量较低节点转入睡眠状态，使得活跃节点的平均能量逐渐接近最佳能量，优于ECC、CVT活跃节点的平均能量。ECC活跃节点相对减少，但是边界节点比率相对增多，边界节点的能量不一定最优，使得ECC活跃节点的平均能量先逐步增大、后呈下降趋势，但优于初始网络的节点平均能量。CVT以最小活跃节点数量为目标，没有考虑节点能量因素，CVT活跃节点的平均能量稍低于初始网络的节点平均能量。

5.6 算法性能分析

5.6.1 分布式调度收敛性

通信相邻、局部Voronoi不相邻的节点可以同步执行Voronoi冗余识别，通信相邻的节点异步执行ECC的冗余识别，使得DVC调度收敛性(即节点确定最终状态的循环迭代次数)优于 ECC；例如，图 12(a)、图 12(b)给出实验场景 Rs=100、n=1 000中DVC与ECC的循环迭代次数；随着节点数量n或传感半径Rs的增加，通信邻居数量将显著增加，DVC与ECC的迭代次数分别增多；其中，DVC的最大、平均迭代次数分别不超过42、9，而ECC的最大、平均迭代次数分别大于、接近通信邻居数量。

5.6.2 时间性能

假设不考虑消息交互、等待时间，使用所有节点的计算时间总和分析算法时间性能；随着节点数量n或传感半径Rs的增大，通信邻居数量显著增加，延长了DVC、ECC的计算时间；但是Voronoi冗余识别与节点密度无关，使得DVC计算时间略优于ECC，如图12(c)、图12(d)所示。CVT基于Voronoi划分的冗余识别时间与节点数量相关、与传感半径Rs无关，CVT计算时间随着节点数量n近似指数增长，如图12 (c)所示；网络覆盖整个目标区域后，传感半径Rs基本上不影响CVT计算时间，如图12 (d)所示；总的来说，CVT计算时间要大于DVC与ECC。

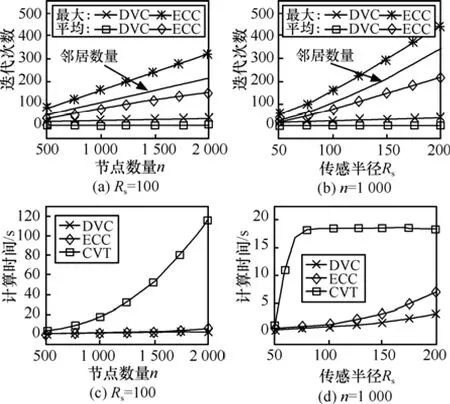
图12 算法性能分析

6 结束语

在传感器网络覆盖部分目标区域的假设条件下，提出一种基于局部Voronoi区域的冗余识别规则，其计算时间复杂度与节点密度无关；在维持网络原有覆盖质量的情况下，提出一种能量优先的Voronoi调度规则，对算法正确性进行了理论分析。仿真实验表明，本文算法求解活跃节点的数量、平均覆盖度，接近集中式CVT算法、优于分布式ECC算法；而活跃节点的平均能量、调度收敛性以及算法时间性能优于CVT算法与ECC算法。下一步将重点考虑Rc＜2Rs、k度覆盖(k≥2)以及三维环境下的Voronoi覆盖控制问题。

[1] 孙利民, 李建中, 陈渝. 无线传感器网络[M]. 北京∶ 清华大学出版社,2005.SUN L M, LI J Z, CHEN Y. Wireless Sensor Networks[M]. Beijing∶Tsinghua University Press, 2005.

[2] YICK J, MUKHERJEE B. Wireless sensor network survey[J]. Computer Networks, 2008, 52∶2292-2330.

[3] 任彦, 张思东. 无线传感器网络中覆盖控制理论与算法[J].软件学报, 2006,17(3)∶422-433.REN Y, ZHANG S D. Theories and algorithms of coverage control for wireless sensor networks[J]. Journal of Software, 2006, 17(3)∶422-433.

[4] TIAN D, GEORGANAS N D. A coverage-preserved node scheduling scheme for large wireless sensor networks[A]. Proc of First International Workshop on Wireless Sensor Networks and Applications[C].2002. 32-41.

[5] YI Z, KRISHNENDU C. A distributed coverage and connectivity-centric technique for selecting active nodes in wireless sensor networks[J]. IEEE Transactions on Computer, 2005, 54(8)∶978-991.

[6] HUANG C F, TSENG Y C. The coverage problem in a wireless sensor networks[A]. Proc of the ACM Int'1 Workshop on Wireless Sensor Networks and Applications[C]. 2003.115-121.

[7] NURCAN T, WANG W Y. Effective coverage and connectivity preserving in wireless sensor networks[A]. Proc of IEEE Conf on Communication and Networks[C]. 2007. 3388-3393.

[8] VIERA M A M, VIERA L F M. Scheduling nodes in wireless sensor networks∶ a voronoi approach[A]. Proc of 28th Annual IEEE International Conf on Local Computer Networks[C]. 2003.423-429.

[9] 蒋杰,方力.无线传感器网络最小连通覆盖问题求解算法[J]. 软件学报, 2006,17(2)∶175-184.JIANG J, FANG L. An algorithm for minimal connected cover set problem in wireless sensor networks[J]. Journal of Software, 2006,17(2)∶175-184.

[10] CARBUNAR B, GRAMA A. Coverage preserving redundancy elimination in sensor networks[A]. Proc of First Annual IEEE Communications Society Conf on Sensor and Ad Hoc Communications and Networks[C]. 2004.377-386.

[11] 陆克中. 无线传感器网络中的数据收集问题研究[D]. 中国科学技术大学, 2007.70-76.LU K Z. Research on Data Collection in Wireless Sensor Networks[D].University of Science and Technology of China, 2007.70-76.

[12] BALISTER P, ZHENG Z. Allowing coverage holes of bounded diameter in wireless sensor networks[A]. Proc of IEEE INFOCOM[C].2009.136-144.

[13] 苏瀚, 汪芸. 传感器网络中无需地理信息的空洞填补算法[J].计算机学报, 2009, 32(10)∶1957-1970.SU H, WANG Y. A self-healing algorithm without location information in sensor networks[J]. Chinese Journal of Computer, 2009,32(10)∶1957-1970.

[14] OKABE A, BOOTS B. Spatial Tessellations∶ Concepts and Applications of Voronoi Diagram[M]. New York∶ John Wiley & Sons, 1999.

[15] ZHANG C, ZHANG Y C. Localized algorithms for coverage boundary detection in wireless sensor networks[J]. Wireless Networks, 2009,15(1)∶3-20.