基于最小二乘优化的车辆位置估计算法

彭鑫，李仁发，杨柳，刘 骄

(湖南大学 计算机与通信学院，湖南 长沙 410082)

1 引言

近年来，道路交通安全已是智能交通系统(ITS,intelligent transportation systems)所要解决的头号问题。车载自组网作为智能交通系统的重要基础引起了学术界和工业界的极大兴趣。

车载自组网是由车辆和布设在特定位置的路边单元(RSU)所组成的开放式移动自组织网络(MANET)[1]。它具有部署方便、成本低廉和结构开放等特点，可实现事故预警、辅助驾驶、交通信息发布、车间通信和 Internet接入等服务，有着广阔的应用前景。位置服务是车载自组网诸多应用的基础，比如车辆导航和碰撞避免。另外，车载自组网的路由也需要车辆位置信息[2,3]。目前，GPS导航以其精度高、费用低廉等特点在车载系统中得到了广泛应用。虽然GPS在开阔地带可以取得良好的定位性能，但由于卫星信号容易受到遮挡，GPS无法用于高楼林立的城市中心区和隧道中。现在采用的替代方案是以陀螺仪为代表的车载航位推算系统[4]。从航位推算系统目前的技术水平看，位置估计误差为行驶距离的1%～2%。也就是说，一辆以60英里时速行驶的汽车，GPS信号只要中断30s，车辆的位置估计误差将会大于10m。这样的精度无法满足高安全性位置服务的需要。因此，车辆位置估计将是车载自组网研究的热点问题之一。

本文提出一种基于最小二乘法的车载位置估计算法。提出的方案充分利用了车辆间的距离信息，通过对距离矩阵采用最小二乘法来提高估计精度并且避免了定位滞后问题，满足车网环境下实时定位的性能要求。提出的算法可以直接得到车辆的相对位置分布，而且在有绝对位置信息的条件下可以获得车辆的实际位置。最后通过仿真与文献[5]的算法进行了对比。

本文第2节简述国内外相关研究；第3节建立了车辆位置估计的模型和最小二乘估计方法；第 4节给出了车辆位置估计算法及其复杂度分析；第 5节是仿真和实验分析；第6节是结束语。

2 相关研究

目前已提出的位置估计算法主要面向无线传感器网络。由于节点计算资源的限制，一些估计精度高但计算量较大的算法无法很好地用于无线传感器网络，而车载系统具有丰富的计算资源，有利于高精度位置估计算法的开发。一般来说，位置估计算法可分为粗粒度和细粒度2大类。粗粒度位置估计算法主要利用节点在网络中的连通性关系来确定节点的大致位置[6,7]。细粒度算法通过距离测量等手段可提供更为精确的位置信息[8]。本文出于研究上的考虑，主要研究用于移动自组网环境下的细粒度位置估计算法。

文献[9]提出的移动定位算法要求每个节点测得与一跳邻居间的距离并且建立局部坐标系求出与一跳邻居间的夹角，然后节点对局部坐标系进行变换得到全局坐标系。该算法的不足在于通信开销过大并且扩展性低。文献[10]提出的蒙特卡罗移动定位算法把运动节点的可能位置以加权样本集的形式表示为后验分布，用加权样本集作为节点的位置估计。该算法在滤波阶段需要锚节点直接支持，不能直接得到周围节点的运动情况，制约了算法在车载环境下的应用。文献[11]利用移动节点在网络中添加采样点，然后利用多维尺度变换来实现移动定位。文献[12]提出一种基于点模式匹配的车辆位置估计算法。该算法维持一个地标拓扑数据库，然后车辆对周围环境的地标进行识别，用识别到的三角拓扑与库中的拓扑进行匹配来确定车辆位置。该算法要求车辆配备激光扫描器，并且主要面向单台车辆的自身位置估计。文献[13]提出了一种车载定位算法，它根据定位需要进行建簇，然后利用三边定位得到簇内车辆的相对位置。但是该算法在测距过程中存在明显的误差扩散问题无法保证估计精度。文献[5]提出的分布式位置估计算法通过对初始位置估计采用最小二乘法来求得车辆位置分布。该算法在得到车辆位置分布的同时保证了较好的估计精度，是目前典型的车载分布式位置估计算法。

上述车辆位置估计方法有一个共同点，就是通过对运动车辆的瞬时估计把动态网络转化为静态问题来求解。在一般移动自组织网络环境下，这种方法是可行的，但是在车辆高速运动的车载网络环境下，采用这种模式将会导致定位滞后问题，降低了估计精度，无法满足实时性要求。

3 算法模型的建立

3.1 车辆位置估计模型

本文算法通过测量车辆间的距离信息求出车辆位置的最佳估计。令ρij表示车辆i和j之间的测量距离，Xn,m表示车辆的坐标矩阵，n表示车辆数，m表示空间维度，dij表示车辆i和j在m维空间X中的距离：

对于n阶距离矩阵A，定义中心化映射：

其中，In表示 n阶单位矩阵，令根据多维尺度变换[14]，有如下定理。

定理1 矩阵P为 m维空间中点间平方距离矩阵，当且仅当矩阵π(P)为对称半正定矩阵，并且有分解式π(P)=XXT，其中X为n×m的空间点坐标矩阵，使得D2(X)=P。

定理2 如果矩阵P为 m维空间中点间平方距离矩阵，B=π(P)，r=rank(B)，λ1≥…≥λr≥λr+1=…=λn=0表示矩阵B的奇异值，Λ=diag(λ1…λn)，则有分解式B=QΛQT。在m维空间中，令Λm=diag(λ1…λm)，Qm表示矩阵Q的前m列，则X=QmΛm1/2。

上述定理实际上给出了由空间中点间距离计算各点坐标的方法。基于多维尺度变换的无线传感器网络定位算法[11,15]就是以上述结论为基础。

从定理中不难看出，要得到网络中节点的坐标，必须准确获得各节点之间的距离，构成距离矩阵。这在静态无线传感器网络中易于满足，在移动自组织网络中可以通过对移动节点的运行轨迹进行采样，将动态网络转化为静态网络进行定位。但在车载自组网中，车辆运动速度非常快，如果仍然通过对车辆运动轨迹采样的方式进行位置估计将造成车辆的估计位置滞后于实际位置，导致估计精度的下降，无法满足实时性要求。本文算法将车辆的运行时间划分为连续的时间段，从而把车辆位置估计问题转化为多约束联合优化问题，然后通过迭代最小二乘法求解。

下面考察2种交通模型。如图1所示，在t0时刻，测得车辆i、j之间的距离为r0，与行驶方向间的夹角为α，车辆i、j的行驶速度分别为vi、vj。不难算出，图1(a)中，t1=t0+τ时刻，车辆i、j之间的距离为

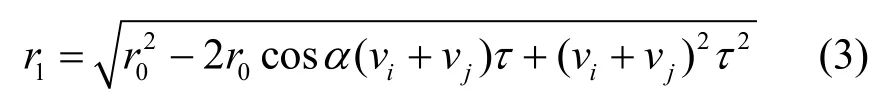
图1 2种交通路段

图1(b)中，t1=t0+τ时刻，车辆i、j之间的距离为

其中，μ=(r0sinαi-vjτsinθ)/sinθ，ω=(r0sinαj- viτsinθ)/sinθ，θ=π-αi-αj。在[t0,t1]时间段内，i、j之间的距离 δij∈[min(r0,r1), max(r0,r1)]，车辆距离矩阵满足条件Δ0≤Δ≤Δ1，其中，

图1的车辆运动模型适用于车辆由远及近或由近及远的情况。另一运动模型是在时间τ内，两车因距离过近运动状态发生了改变，即从由远及近变为由近及远，两车间的最短距离出现在(t0, t1)内。由于本文选取的τ为很短的时长，仅当两车距离很近时才有这种状况发生，此时虽然但是两者非常接近。为计算方便和统一模型，本文不考虑这种情况。

因此，根据以上分析，车辆位置估计问题可转化为多约束联合优化问题：

本文采用迭代最小二乘法来求解上述问题。

3.2 车辆位置估计的最小二乘法

根据问题(5)，分别定义最小二乘迭代函数f1(Δ)与f2(D)。

函数 f1(Δ)：

step2 对矩阵B进行奇异值分解。B=QΛQT，在 m 维空间中，令Λm=diag(λ1…λm)，Qm表示矩阵Q的前m列，则

这样函数 f1和 f2构成了问题(5)的 2个迭代过程。接下来讨论该迭代过程的收敛性。首先证明一个定理。

定理 3 距离矩阵约束条件 Sn=[Δ0,Δ1]是一个凸集。

不失一般性，假设r0≥r1。

令矩阵 M1=[m1ij], M2=[m2ij]，且 M1, M2∈Sn，即min(r0,r1)2≤m1, m2≤max(r0,r1)2。由不难得到

因此，Sn是一个凸集。

证毕。

令{Δk}为f1和f2迭代过程所产生的序列，En表示n阶距离矩阵的集合。不难看出，函数f1完成了从Sn到En子集上的映射，函数f2完成了从En子集到Sn的映射。将式(2)定义的映射π应用于问题(5)，令 B=π[D(X)]，根据定理 1，式(5)可以表示为如下形式：

其中，P(n)表示n阶半正定矩阵的集合。

令Δ∈Sn，b∈P(n)，将函数 f1的 step2～setp4 重新定义为函数D=φ(b)。由此构建问题(6)的迭代过程分别为 F1=πf1(Δ)，F2=f2φ(B)，并且 G(Δ)=F2F1(Δ)。不难看出，F1为距离矩阵所构成的凸集到半正定矩阵集合上的映射，F2为半正定矩阵到一个凸集上的映射。通过函数 G(Δ)可得到问题(6)的迭代序列{Δk}=G(Δ0)。对于∀Δa∈Sn，有 Ba=F1(Δa)，Δα=F2(Ba)，Δα∈G(Δa)。因此可得到如下不等式：

由F2为半正定矩阵到凸集上的单射可知F2(Ba)是唯一的。如果F2(Ba)=Δa，则取

如果Δa∈G(Δa)，则取

在Sn上定义子集：

由定理3可知，Sn是一个闭凸集，所以集合N是有界的。由式(8)可知{Δk}=G(Δ0)⊆N，再由不等式(7)可得{Δk}=G(Δ0)在Sn上是收敛的。令Δn为序列{Δk}的收敛点，有Δn=G(Δn)。由于函数F1为距离矩阵所构成的凸集到半正定矩阵集合上的映射，因此，{Bk}=F1(Δ0)也是有界的并且为收敛序列。

综上，由 F1，F2构成的问题(6)的迭代序列是收敛的并且有唯一收敛点(Δn,F1(Δn))。问题(6)与问题(5)是等价的，所以函数f1，f2所构成的迭代序列在问题(5)上也是收敛的。

4 基于迭代最小二乘的车辆定位算法

4.1 算法描述

本文提出的车辆位置估计算法描述如下。

step1 在t0时刻，每台车辆测量与周围邻居间的距离 r0和夹角α，并广播行驶速度 v，选取合适的τ值，根据式(3)或式(4)求得r1；

step2 通过Dijkstra算法求得车辆2跳邻居间的距离和以及t0时刻的距离矩阵；

step4 令 k=1，由函数 f1(Δ0)得到矩阵 D(X0)；

step5 对矩阵 D(Xk-1)使用函数 f2(D(Xk-1))求得Δk；

step6 对矩阵Δk使用函数 f1(Δk)得到矩阵D(Xk)；

step7 若‖Δk-D(Xk)‖≤ε，转到step8；否则，k=k+1，转到step5；

step8 根据每台车辆得到的相对位置Xk，逐步添加与其有最多共同节点的局部坐标图，直至得到全网相对坐标；

step9 如果有3台以上车辆已知绝对位置，则可由Householder变换将相对坐标Xk转化为绝对坐标。

4.2 算法分析

根据驾驶行为规律，车辆在道路上会按特定方向定速巡航，而且τ本身也是较小的时间段。因此算法step1中，使用t0时刻的速度v来计算t1=t0+τ时刻的车辆间距是合理的，而且避免了车辆相对运动状态的改变。由于车辆依据道路规划行驶，而非随机分布，因此 step2采用最短路径长度来近似车辆距离可以保证较好的测距精度。为了保证实时性要求，本算法并未求出问题(5)的最优解，而是在step7中设定一个阈值ε，当问题(5)满足ε条件时终止迭代。对于车辆的某些安全应用而言，比如碰撞避免，无需求得车辆绝对位置，只要在 step8中求出周围车辆的相对位置即可。

如果车辆的连通度为c，车辆数为n，k为算法平均迭代次数，a为信标车辆的数目。算法 step1的复杂度为 O(c2)。step2的复杂度为 O(c3)。step3-step7的复杂度为 O(kc3)。step8的复杂度为O(c3n)。step9的复杂度为 O(a3+n)。因此算法总复杂度为O(c3n+kc3+a3)。

5 仿真分析

本文模拟2种交通环境。一种是直线路段，另一种是交叉路段。采用MATLAB7.1与文献[5]的算法进行了比较。实验中距离测量引入零均值高斯噪声 N(0,σ2)。算法 step7的迭代终止条件ε=10-3。用均方根误差(RMSE)作为性能评价指标:

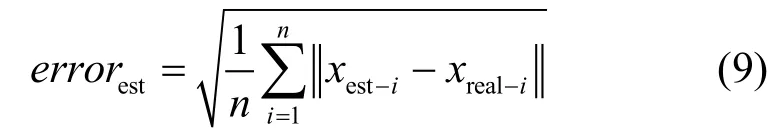
其中，n是阴影区域内车辆总数。

5.1 仿真实验1

如图2所示，模拟2km长的双向6车道路段，其中阴影区域1km长路段表示无法获取GPS信号的区域，也就是需要进行位置估计的区域。阴影区域两侧各有 0.5km的路段，其中的车辆可以估计自身的绝对位置，从而为阴影区域内车辆的位置估计提供支持。仿真区域随机分布300台车辆，行驶速度保持 60km/h。上方路段由右向左行驶，即从右端随机进入仿真区域，从左端离开仿真区域，下方路段则反之。

图2 双向6车道交通

GPS定位采用标准差为7m的高斯误差模型，每秒刷新一次位置信息，取τ=1s，并且位置估计采用地图匹配法，将车辆的估计位置限制在当前车道上。文献[5]算法初始位置估计采用三边测量法。车辆通信距离r=130m，车辆测距标准差σ=3m。记录场景中某台车辆的实验结果如图3所示，上方曲线为GPS的估计精度，中间曲线为文献[5]算法的精度，下方曲线为本文算法的估计精度。从图中可以看出，GPS外加地图匹配的估计误差约为6.9m，文献[5]算法的估计误差为4.7m，本文算法的位置估计误差为3.4m。

图3 3种位置估计算法的误差比较

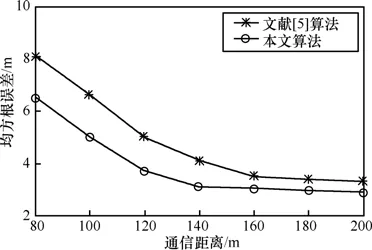
图4 2种算法在不同通信距离下的误差比较

在上述环境中，改变车辆通信半径，比较2种算法在不同通信半径下的估计精度。实验结果取10次运行的平均值。如图4所示，2种算法随着通信半径的增大估计误差显著下降。对文献[5]算法而言，通信半径越大周围邻居越多，在三边测量阶段能够取得更好的精度，在求精阶段可更准确地估计邻居车辆的位置。本文算法，通信半径越大，最短路径距离近似方法引入的误差也就越小，而且在最小二乘过程中的距离值也越精确。从图中可以看出，在当前实验环境中，文献[5]算法当通信半径大于150m时性能趋于稳定，本文算法当通信半径大于120m时性能趋于稳定，并且比文献[5]算法有更好的估计精度。

在相同环境中，改变车辆测距误差比较2种算法在不同测距误差下的性能。结果如图 5所示。2种算法都以距离信息为基础，因此在车辆测距误差增大的情况下，算法的估计误差都呈增大趋势。由于本文算法可以通过最小二乘迭代过程求得一个凸集范围内的最优解，因此取得了比文献[5]算法更好的估计精度。

图5 2种算法在不同测距误差下的比较

5.2 仿真实验2

如图6所示，模拟2km长的双向四车道路段，其中车道1和4各有一条长0.5km的辅道单向出口以评估算法在交叉路段的性能。图中阴影区域的1km长路段表示进行位置估计的区域。阴影区域两侧各有0.5km的路段，其中的车辆可以获知自身的绝对位置。仿真区域随机分布220台车辆，行驶速度保持60km/h，车道1和4的车辆从辅道离开。上方路段由右向左行驶，也就是右端随机进入仿真区域，从左端离开仿真区域，下方路段则反之。

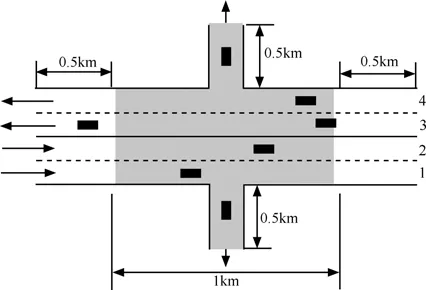
图6 交叉路段

本次实验采用和实验1相同的参数。首先改变车辆通信半径与文献[5]比较，结果如图 7所示。然后设置车辆通信半径r=130m，改变车辆测距误差，结果如图8所示。从图7和图8不难看出，在交叉路段环境中，2种算法位置估计精度比直线路段略有下降。这是由于文献[5]采用三边测量法，在交叉路段环境中容易出现反褶的不定性。虽然该算法采用多次测距来进行弥补，但在交叉路段车辆的距离估计精度难以保证。本文采用最短路径距离来估计2跳车辆间的距离，这种方法在直线路段可取得较好的结果，但在交叉路段精度有所降低。总体上看，本文算法在交叉路段环境中性能稳定，仍然取得了较好的精度。

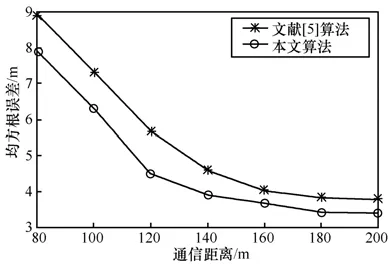
图7 交叉路段环境下，算法在不同通信距离的比较

图8 交叉路段环境下，算法在不同测距误差时的比较

6 结束语

针对车辆位置服务要求精度高、实时性强的特点提出了基于最小二乘法的车辆位置估计算法。该算法充分利用车辆行驶速度和车辆间的距离信息推导车辆距离矩阵所满足的凸约束，然后采用最小二乘法进行车辆位置估计，从而避免了定位滞后问题引入的误差。实验分析表明，本文算法在满足车辆实时位置估计的同时，能有效地提高估计精度，并且在不同道路环境下表现出较强的适应性和可靠性。

[1] BLUM J, ESKANDARIAN A, HOFFMAN L. Challenges of inter-vehicle ad hoc networks[J]. IEEE Transactions on Intelligent Transportation Systems, 2004, 5(4)∶ 347-351.

[2] BOUKERCHE A, OLIVEIRA H A B F, NAKAMURA E F. Vehicular ad hoc networks∶ a new challenge for localization-based systems[J].Computer Communications, 2008, 12(31)∶2838-2849.

[3] 常促宇,向勇,史美林.车载自组网的现状与发展[J]. 通信学报, 2007,11(28)∶ 116-126.CHANG C Y, XIANG Y, SHI M L. Development and status of vehicular ad hoc networks[J]. Journal on Communications, 2007, 11(28)∶116-126.

[4] KING T, FUBLER H, TRANSIER M, et al. Dead-reckoning for position-based forwarding on highways[A]. Proceedings of the 3rd International Workshop on Intelligent Transportation[C]. Hamburg, Germany, 2006. 199-204.

[5] PARHER R, VALAEE S. Vehicle localization in vehicular networks[A]. IEEE 64th Vehicular Technology Conference[C]. Canada,2006.2713-2717.

[6] BULUSU N, HEIDEMANN J, ESTRIN D. GPS-less low cost outdoor localization for very small devices[J]. IEEE Personal Communications Magazine, 2000, 5(7), 28-34.

[7] DOHERTY L, GHAOUI L E, PISTER K. Convex position estimation in wireless sensor networks[A]. Proceedings of INFOCOMM[C]. Anchorage, USA, 2001. 1655-1663.

[8] RUDAFSHANI M, DATTA S. Localization in wireless sensor networks[A]. Proceedings of IPSN[C]. Cambridge, USA, 2007. 51-60.

[9] CAPKUN S, HAMDI M, HUBAUX J P. GPS-free positioning in mobile ad-hoc networks[A]. Proceedings of the 34th International Conference on System Sciences[C]. Hawaii, USA, 2001.9008-9018.

[10] BAGGIO A, LANGENDOEN K. Monte-carlo localization for mobile wireless sensor networks[J]. Ad Hoc Networks, 2008, 5(6)∶ 718-733.

[11] WU C H, SHENG W H, ZHANG Y. Mobile sensor networks self localization based on multi-dimensional scaling[A]. Proceedings of IEEE International Conference on Robotics and Automation[C]. Roma,Italy, 2007. 4038-4043.

[12] HAUNERT J, BRENNER C. Vehicle localization by matching triangulated point patterns[A]. Proceedings of the ACM International Conference on Advances in Geographic Information Systems[C]. Seattle,USA, 2009. 344-351.

[13] KUKSHYA V, KRISHNAN H, KELLUM C. Design of a system solution for relative positioning of vehicles using vehicle-to-vehicle radio communications during GPS outages[A]. Proceedings of IEEE Vehicular Technology Conference[C]. Dallas, USA, 2005. 1313-1317.

[14] BORG I, GROENEN P. Modern Multidimensional Scaling∶ Theory and Applications[M]. New York∶ Springer-Verlag, 1997.53-59.

[15] SHANG Y, RUML W, ZHANG Y. Localization from connectivity in sensor networks[J]. IEEE Transactions on Parallel and Distributed Systems, 2004, 15 (11)∶ 961-974.