WEP数据加密协议的两种改进攻击

孙思维，胡磊

（中国科学院研究生院 信息安全国家重点实验室，北京 100049）

1 引言

WEP协议是IEEE 802.11无线局域网标准[1]中的数据加密协议，在现实生活中的无线局域网中被广泛使用，对其安全性分析是近年来研究的热点。2001年，Borisov、Goldberg和Wagner首次对WEP协议进行了分析[2]，他们的分析揭示了WEP协议在保护数据完整性和机密性上的一些重大缺陷。同年，Fluhrer、Mantin和 Shamir[3]针对 WEP协议中RC4流密码的使用不当，提出了一个恢复WEP密钥的已知明文攻击（以下称为FMS攻击）。此后，研究人员又发现了更多的攻击方法，如 chop-chop攻击[4]、KoreK 攻击[5]、Klein 攻击[6]和 PTW 攻击[7]，等等。FMS攻击和chop-chop攻击是2类最重要的攻击方法，其中，chop-chop攻击是所有主动型WEP攻击的基础。这一切都表明，WEP加密协议的设计存在着严重缺陷。到目前为止，国际标准 WEP已被 WPA替换，但是出于经费等原因，市面上的多数无线接入点仍然使用 WEP协议。由于现今一些高效WEP攻击需要向网络中大量广播伪造的ARP数据分组，许多入侵检测系统可以迅速地发现那些主动攻击者。这使得改善原有的被动型WEP攻击变得很有意义，这是本文研究的一个出发点。

在本文的第3节中，描述chop-chop攻击，并给出它的一个改进，此改进不仅提高了 chop-chop攻击的速度，也减少了攻击所需向网络中发送的WEP数据帧的数量。在第4节中，分析RC4流密码在WEP协议中的使用细节，给出原始的FMS攻击。在第5节中，提出被动型的WEP攻击，即FMS攻击的一个改进方法——FMS+攻击，理论分析表明，FMS+攻击具有更高的成功率，并给出具体的实验数据。

2 WEP协议概述

在 WEP协议中，无线接入点和每个合法客户端共享一个 WEP密钥 R。当数据发送端要发送明文M时，它首先计算M的32bit校验值CRC32(M)，选择一个初始向量V，然后用V||R作为RC4流密码的密钥生成密钥流 X = RC4(V||R)去加密M||CRC32(M)，即密文为

最后，发送者发送的数据为 V||C，称为一个 WEP数据帧，C为WEP数据帧的加密部分。当接收端收到WEP数据帧时，通过计算

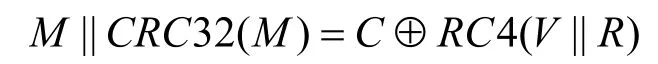
得到明文M。

这里需要指出的是，每个从客户端发送到客户端的 WEP数据帧通常都是由无线接入点转发的。当无线接入点接收到WEP数据帧V||C后，它首先对V||C的加密部分进行解密，然后对解密后的数据进行 CRC32完整性检测。如果通过检测，它就对WEP数据帧V||C进行转发，否则丢弃此数据帧。下节的chop-chop攻击正是利用了无线接入点的这个转发特性。

3 chop-chop攻击及其改进

在 WEP协议中，每个数据被看作一个二元序列，同时被看作二元域 F2上的一个多项式，例如，二元序列 100111101被看成多项式 x8+ x5+ x4+x3+ x2+ 1。下面将等同地看待二元序列和上的多项式。一个二元序列P可以通过CRC32检验，当且仅当它的多项式满足

其中，J =x31+x30+…+1对应32bit全1二元序列，f = x32+ x26+ x23+ x22+ x16+ x12+ x11+ x10+ x8+x7+ x5+ x4+ x2+ x +1 是上的一个32次不可约多项式。由式(1)可以得出 M 的校验值 CRC32(M)的计算方法：因为 M ||C RC 3 2(M )通过校验，即Mx32+CRC 3 2(M ) = J ( mod f )，所以有

通过式(2)可由 M 计算出唯一的 32bit序列CRC32(M)。

如果用 Pi表示P的最后i位，Qi表示二元序列P去掉最后i位所形成的二元序列，则有

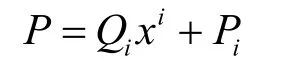
因为f是一个不可约多项式，对于 F2上任意多项式 g ≠ 0 (modf)，可以计算出唯一的小于32次的多项式，记为 g-1，使得 g-1g = 1 (mod f)。下面给出一个简单性质。

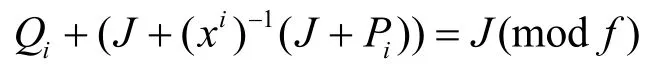
第1步 攻击者截获一个WEP数据帧V||C。

第2步 攻击者去掉 C = (M || C RC3 2(M )) ⊕X的最后i位，此时得到的二元序列记为。令 Qi为M | |C RC 3 2(M )去掉最后i位得到的二元序列， Xi为X去掉最后i位得到的二元序列，即 Xi是一个缩短的密钥流。

第3步 攻击者随机猜测 P = C⊕ X = (M|| C RC32(M ) )的最后 i位为，然后计算= J +(xi)-1(J +Pi) (mod f )，并把作为新的WEP数据帧发送给接入点。

下面给出改进的chop-chop攻击，并给出此攻击的理论分析。原始的以代码形式给出的chop-chop攻击[4]实质上是上述攻击 i = 8 的情形，此时当攻击者进行到chop-chop攻击的第3步时，它需要猜测一个 8bitP8并向接入点转发数据帧由第2节中最后一段的讨论可知，当接入点接收到这个数据帧后首先解密得到，然后对进行CRC32完整性检测。如果攻击者正确地猜到了P8的真实值，检测通过，接入点便转发攻击者构造的数据帧。这样，在第4步中，攻击者会发现接入点的这个行为，从而知道它自己已经正确地猜测到了8P。然而，在第3步中，攻击者平均要进行82/2 128= 次猜测才能猜到真实的8P，而当它猜错时，由于检测不到接入点转发的数据帧，它必须重复第3步。

实际上，在chop-chop攻击中，如果取 i =1，则在进行到第3步时，真实的 P1只可能为1或者0，不妨在每次进行到第3步时，都猜测 P1为0。那么在进行到第4步时，如果攻击者监听到接入点转发的，那么显然，它在第3步时正确地猜到了 P1，如果它没有监听，说明它猜错了，然而此时的 P1只有2种可能，所以攻击者此时并不需要重新进行第3步，而是直接确定出真实的 P1一定为1。也就是说，当取 i = 1时，攻击者每发送1个数据帧就一定可以解密1bit数据，而当i= 8 时，攻击者平均要进行128次才能猜到真实的8bitP8，即平均每发送16个数据帧才能正确地解密出1bit数据。可见，当 i = 1时，其攻击效率是原始的 chop-chop攻击的 16倍。对密文依次剪切 1bit并执行上述攻击，可以恢复明文的所有数据位。

4 FMS攻击

WEP协议中RC4流密码的使用比较特别，即RC4的密钥K是通过V与R的简单链接V||R得到的。WEP协议中规定V为3byte，由第2节中的描述可知，这3byte的V是攻击者知道的。2001年，Fluhrer、Mantin和Shamir发现这样使用RC4是危险的[3]，一个被动监听网络的攻击者在得到足够多的 WEP数据帧后，可以通过它们的攻击以很大的概率恢复WEP密钥R。

4.1 RC4流密码算法

RC4是一个密钥长度可变，面向字节操作的流密码。图1给出了 RC4算法的描述，其中加法在Z256上进行。RC4算法的实现非常简单，它包括RC4-KSA与RC4-PRGA 2部分。RC4-KSA首先将一个由 256byte组成的状态向量 S初始化为[0,1,…,255]，然后利用密钥K，对状态向量S进行256次置换。每次置换时，首先用i、j标识出状态向量S中的2个元素S[i]与S[j]，然后对换S[i]与S[j]的位置，即新的S[i]和S[j]为原来的S[j]和S[i]，其他位置的元素保持不变。

当 RC4-KSA完成对 S的 256次置换后，RC4-PRGA利用所得状态向量不断地输出密钥流字节。在每次输出密钥流字节前，都要对S进行一次新的置换。例如，当RC4输出其第一个密钥流字节时，状态向量S共经历了257次置换。下面的讨论采用如下记号：

1) 用0,…,255表示全部的单字节值，即把每个字节看成Z256中的一个元素。

2) 用S0表示状态向量S刚经过RC4-KSA Initialization后S的状态，即此时有S = [0,…,255]。用S-1[i]表示满足S[j] = i的j值。

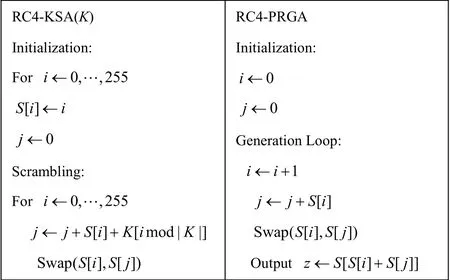
图1 RC4流密码算法

3) K表示RC4算法的密钥。特别地，在WEP协议中，K = V||R，其中，V是3byte的初始向量，R是WEP密钥。

4) X表示RC4算法输出的密钥流，X[0]表示X的第 0个字节，X[0,…,u]表示 X的第 0到第 u个字节。

5) 用Sk表示经过k次Swap对换后的状态向量S，S的第k次置换也称为RC4算法的第k步，用ik，jk表示在第k次Swap对换发生的位置，即S[ik]与S[jk]发生了对换。

下面以K = [23,42,232,11]为例，给出RC4算法的具体运算步骤。首先是RC4-KSA：

初始化

?

i0= 0 , j0=0

第1步

?

i1= 0 , j1=23

第2步

?

i2= 1 , j2=66

……

接下来是RC4-PRGA：

第257步

?

i257= 2 , j257= 4 0，并输出 X[0]= 8 5。

另外，通过RC4-KSA算法描述的Scrambling部分，可以得到如下等式：

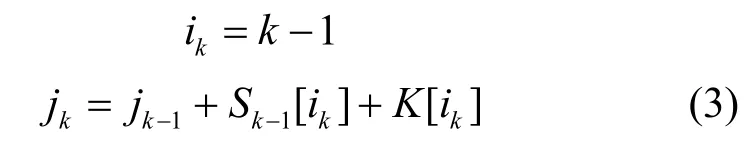
而通过RC4-PRGA，还可以得到RC4算法输出的第一个字节为 S257[ S257[ 1]+ S257[ S256[1]]]。

4.2 FMS条件与攻击

下面给出 FMS攻击的具体描述：首先攻击者监听网络，收集足够多的明密文对，即知道足够多的形如(V,X[0])的数据对，这里V是变量，R是常量。FMS攻击假设攻击者知道密钥K的前l个字节。初始假设l = 3，因为在WEP协议中，攻击者知道K[0]= V[0]，K[1] = V[1]，K[2] = V[2]这 3个字节。当它收集到足够多的数据对后，对每一个(V,X[0])，攻击者运行 RC4(V||R)的前 l步。由式(3)可知，RC4算法的前l步只用到了K[0]至K[l-1]的值，所以攻击者可以完成这个运行。接着，它检查状态向量S是否满足如下FMS条件a：

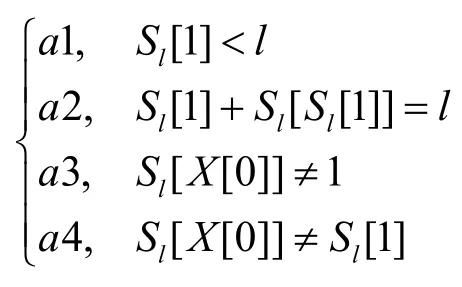
如果不满足上述条件，数据对(V,X[0])就被丢弃，否则，则计算

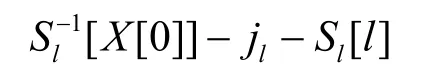
5 改进的FMS攻击

自 FMS攻击被发现以后，又出现了一些新的密钥恢复攻击，然而这些攻击大都要求攻击者知道X[0,…,u]，1u≥ ，或者要求攻击者具有向网络中大量注射 ARP数据分组的能力，而这种行为很容易被入侵检测系统侦测到。本节中将指出，在假设攻击者只能被动监听网络，并且只知道X[0]的情况下，FMS攻击仍能得到改进，将改进后的FMS攻击称为FMS+攻击。

同FMS攻击一样，假设攻击者知道K的前l个字节。攻击者首先要得到大量的 (V,X[0])数据对，利用每个数据对(V,X[0])攻击者运行 RC4算法的前l步，然后检查状态向量S是否满足FMS+条件a：

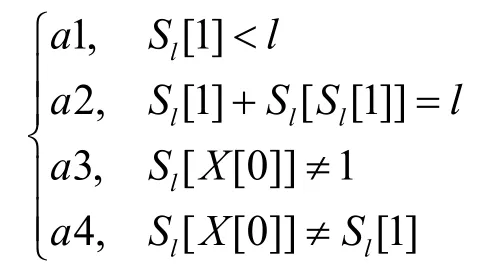
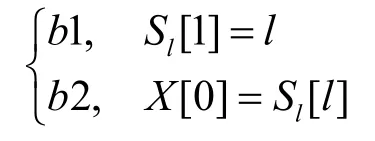
如果满足，则对满足

的K[l]投票；否则，检查是否满足FMS+条件c：

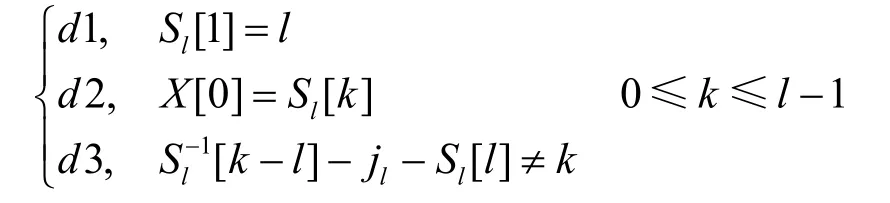
5.1 理论分析

假设当攻击者运行完RC4(V||R)的前l步后，状态向量S满足FMS+条件a1和a2。此时有如下内部状态：

?

对于第l+1步，il+1= l，jl+1=jl+K[l]+Sl[l]，于是S的第l和jl+1个位置的元素被交换，即有如下状态：

?

如果在第l+1步至第256步中，状态向量S的第1、Sl[1]、l个元素没有参与交换，则有

?

对于第257步，i257= 1，j257= S256[1]=Sl[1]，所以有

?

从而，RC4(V||R)输出如下字节：

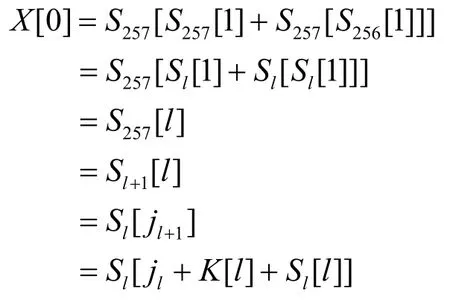
此时有

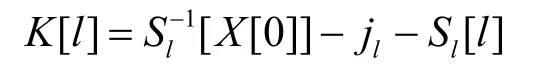
又因为在RC4(V||R)计算的第l+1步至第256步中，Sl[1]和Sl[Sl[1]]没有参与交换，而在第l+2步至第256步中，Sl+1[l]没有参与交换，所以有

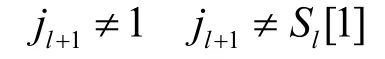
即

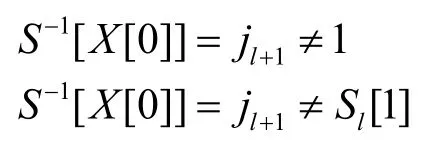
而在第 l+1步至第 256步中，Sl[1]和 Sl[Sl[1]]的位置没有改变，在第l+2步至第256步中，Sl+1[l]的位置没有改变，当且仅当i，j在第l+2步至第256步中不能取到1、l和Sl[1]，而RC4算法从第l+2步开始后，总有 i≥l+1,所以 i不可能取到 1、l和Sl[1](因为 Sl[1]＜l)。

如果把j看成随机的，则j不取1、l和Sl[1](1＜Sl[1]＜l和2＜l)的概率为

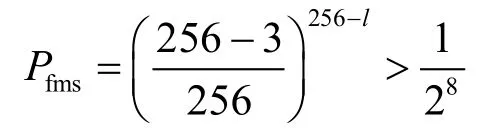
所以，利用满足FMS+条件a计算出的

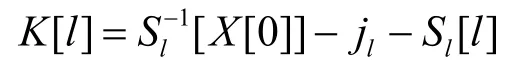
为 K[l]的真实值的概率大于一个取值为随机字节的概率，这是FMS攻击利用这类数据进行投票的原因。

满足FMS条件a的数据只占攻击者所搜集到的数据的很少一部分，大部分数据没有参与投票就被丢弃了，比如在FMS攻击中，满足Sl[1] = l的数据将全部被丢弃。FMS+攻击表明，这类数据不仅不应该被丢弃，而且更具有参与投票的价值。

假设当攻击者运行完RC4(V||R)的前l步后，Sl[1]= l，即

?

对于第l+1步，有

?

如果在第l+2步至第256步中，状态向量S的第1、l和jl+1个位置的元素没有参与交换，则有

?

对于输出的X[0]分2种情况讨论：

1) 若 X[0] = Sl[l]，则

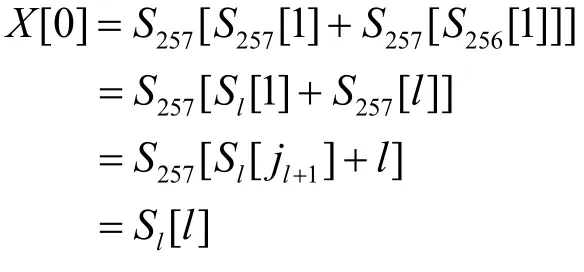
即Sl[jl+1]+l = jl+1，其中，jl+1=jl+K[l]+Sl[l]。同样可以利用 FMS+条件 b的数据计算出的满足Sl[jl+1]+l = jl+1的K[l]的值是K[l]的真实值的概率为Pfms。所以对于这类数据不应该丢弃，也应让其参与到对K[l]的投票中去，同理也可以得到 FMS+条件d。

2) 若 X[0] = l，则

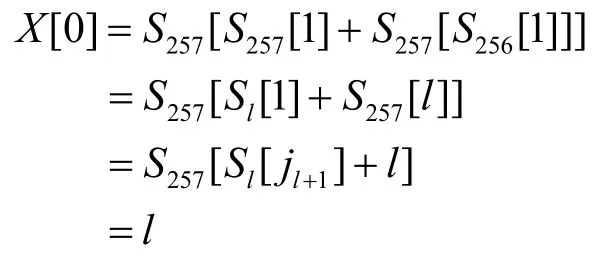
即Sl[jl+1]+l = l或Sl[jl+1] = 0。注意，此时只要求状态向量S的2个位置的元素不参与交换，利用满足FMS+条件c的数据计算出的满足Sl[jl+1] = 0的K[l]的真实值的概率为

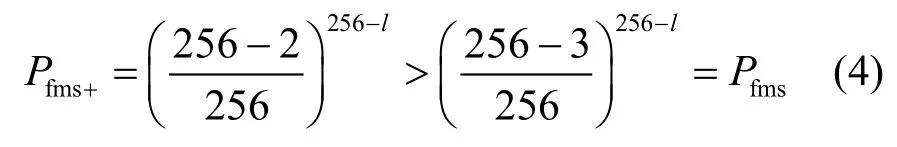
所以说，这类数据更应该参与到对K[l]的投票中去。实际上，Pfms+比Pfms大很多，例如当l = 3时，有

此时Pfms+约为Pfms的2.7倍。利用这类数据投票，可以更容易地区分出K[l]的真实值。

最后指出，随着攻击的进行，攻击者已知的WEP密钥的字节数增多，即l变大，由式(4)可知，Pfms与Pfms+都会随之增加，从而攻击会变得越来越有效。

5.2 实验分析

在实验中，随机生成100个8byte的R（8byte是WEP协议中经常使用的密钥长度），然后对每一个R随机生成一定数量的3byte V，将V||R作为输入，由RC4计算出相应的X[0]。注意FMS攻击和 FMS+攻击是已知明文攻击，这里的“一定数量的X[0]”用于模拟攻击过程中能收集到的明密文对的数量。利用这些(V,X[0])，分别用 FMS攻击与 FMS+攻击猜测 R[0]，统计可用数据帧的数量与正确猜测出R[0]的次数，实验结果见表1。例如，表1的最后一行表示随机生成了100个R，然后对每个 R随机生了 15 000 000个(V,X[0])数据对，在利用这些数据对猜测R[0]时，FMS平均可以利用651个，而FMS+攻击可以利用1 429个；FMS攻击正确地猜测到91个R[0]，而FMS+攻击正确地猜测到98个R[0]。

从表 1可以看出，FMS+攻击将 FMS攻击可以利用的WEP数据帧的数量提高一倍以上。相对于 FMS攻击，FMS+恢复密钥的成功率也有明显提高：当已知60 000至2 000 000个明密文对时，FMS+将FMS攻击恢复WEP密钥第一个字节的成功率提高20%以上。在已知100 000个明密文对的情况下即可以19%的概率恢复出WEP密钥的第一个字节R[0]。

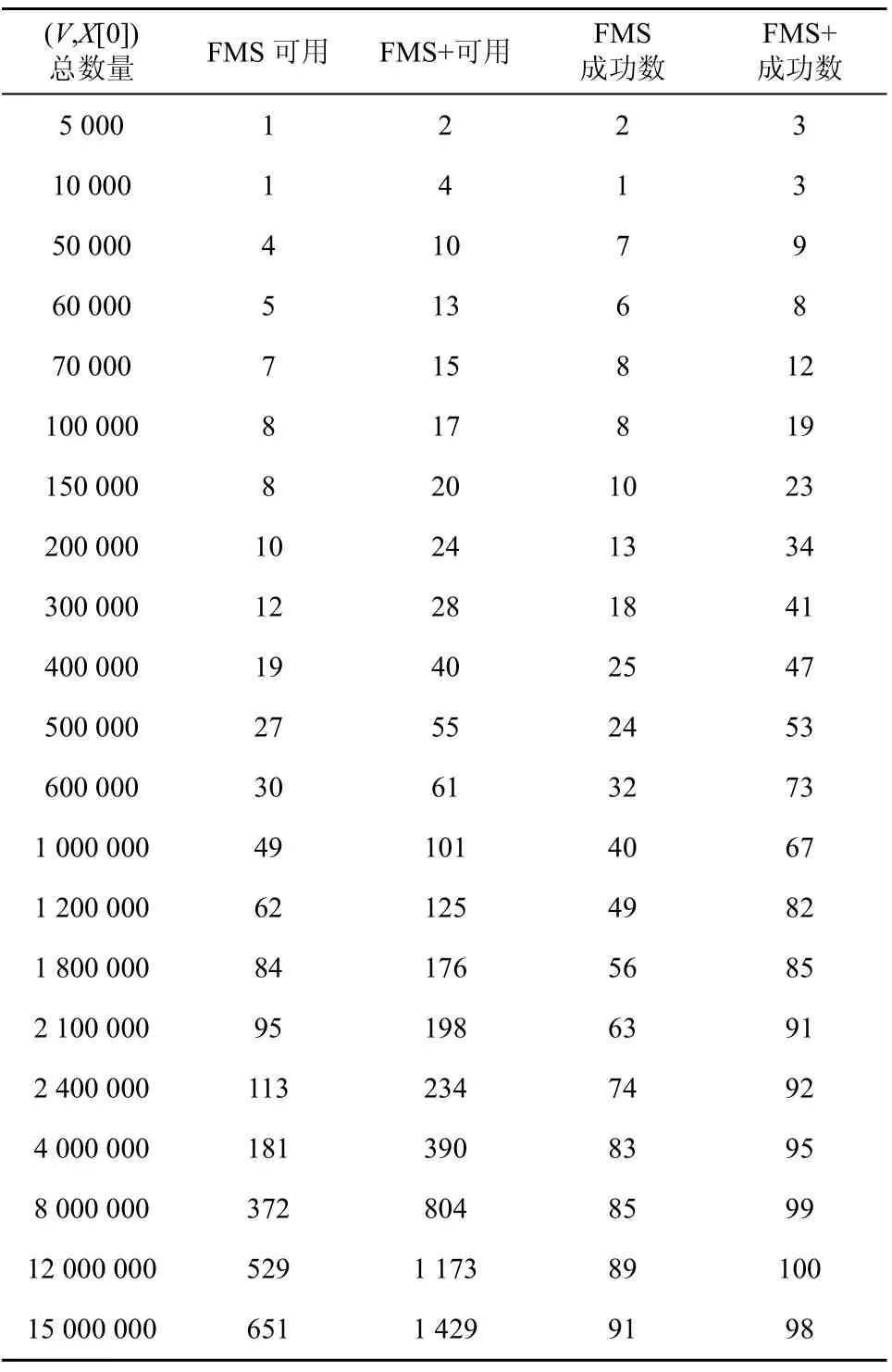
表1 可用(V, X[0])数量与成功恢复R[0]次数比较

在图2中，对FMS与FMS+猜测R[0]的成功率随攻击者收集到的(V,X[0])数据对的数量的变化趋势进行了描述。从图中也可以看出，FMS+攻击显然优于FMS攻击。

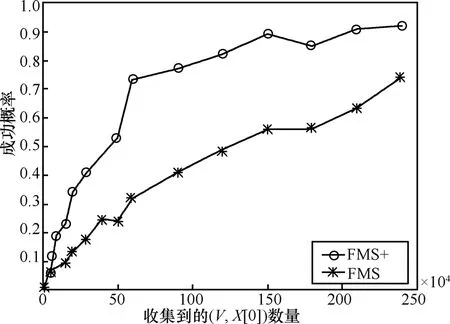
图2 FMS+与FMS猜测R[0]成功率比较

需要指出的是，FMS攻击和FMS+攻击的效率还可以用如下方式提高。在上述实验中，当且仅当得票最多的字节值为真实的R[0]时，才认为一个猜测是成功的。实际上，一个攻击者可以每次猜测出一组R[0]的候选值。比如，可以认为如果R[0]的真实值在得票最多的前2个字节值中，则一次猜测是成功的。这样，实验的成功率可以更高，为取得同样成功率所需的明密文数据可以更少。在实验中，发现R[0]的真实值是得票第二多的字节值的情况经常发生，例如在上述已知 150 000个(V,X[0])数据对的实验中，FMS攻击与FMS+攻击分别有5次和7次出现R[0]真实值是得票第二多的字节值的情况，相比表1第7行后2列的数据“10”和“23”来说，并不是很小。

在攻击中使用的(V,X[0])数据量可以是很大的。保守估计，在一个比较繁忙的网络中，由于多个用户被分成一个用户群而共享一个WEP密钥，攻击者可以每秒收集到 300个(V,X[0])数据对，要收集到10 000 000个这样的数据对也不过10h的时间。攻击者甚至可以通过一些方法使得网络中的流量剧增[10]，从而大大提高收集数据对的速度。

6 结束语

对于WEP加密协议的chop-chop攻击，通过减少每次猜测明文字节的位数，可以明显地提高攻击速度并减少攻击过程中向网络发送的 WEP数据帧的数量，从而提高所有基于chop-chop攻击的主动型WEP攻击的效率。

对于WEP加密协议的FMS攻击，给出的改进方法FMS+攻击可以利用更多的WEP数据帧，从而提高了攻击速度与恢复 WEP密钥的正确率，理论与实验都证明了这一点。据笔者所知，这个改进是目前只利用每个密钥流中一个已知字节就可以恢复 WEP密钥的最好攻击，另外它本身还是一种完全被动攻击，这对真实的攻击者很有意义，一些更高效的攻击（如PTW攻击[7]）需要攻击者主动向网络中广播伪造的 ARP数据分组，而这很容易就会触发入侵检测系统，甚至暴露攻击者的位置。

FMS+攻击还很容易地与其他一些已有的WEP密钥恢复攻击（比如KroeK攻击）结合起来，从而产生更有效的攻击方法。

[1] IEEE, ANSI/IEEE Standard 802.11b∶ Wireless LAN Medium Access Control (MAC) and Physical Layer (Phy) Specifications[S]. 1999.

[2] BORISOV N, GOLDBERG I, WAGNER D. Intercepting mobile communications∶ the insecurity of 802.11[A]. Proceedings of ACM MobiCom 2001[C]. Italy, 2001. 180-189.

[3] FLUHRER S, MANTIN I, SHAMIR A. Weaknesses in the key scheduling algorithm of RC4[J]. Selected Areas in Cryptography , 2001,2559(10)∶ 101-117.

[4] KOREK.Chop-chop experimental WEP attacks [EB/OL]. http∶//www.netstumbler.org/showthread.php?t=12489, 2004.

[5] KOREK. Next generation of WEP attacks?[EB/OL]. http∶//www.netstumbler.org/showthread.php?p=93942&postcount=35, 2004.

[6] KLEIN A. Attacks on the RC4 stream cipher[J]. Designs, Codes, and Cryptography, 2008, 48(3) ∶ 269-286.

[7] TEWS E, BECK M. Practical attacks against WEP and WPA[A].Proceedings of the Second ACM Conference on Wireless Network Security[C]. Zurich, 2009. 79-86.

[8] BITTAU A, HANDLEY M, LACKEY J. The final nail in WEP’s coffin[A]. IEEE Symposium on Security and Privacy[C]. USA, 2006.386-400.

[9] BARON A. Hi-tech heist, how hi-tech thieves stole millions of customer financial records[EB/OL]. http∶//www.cbsnews.com/ , 2007.

[10] 杨哲. 无线网络安全攻防实战[M]. 北京∶ 电子工业出版社, 2008.YANG Z. Practical Wireless Attack and Defense[M]. Beijing∶ Electronic Industry Press, 2008.