用蒙特卡洛模拟法进行库存控制模拟

秦皇岛职业技术学院 范兴昌 赵玉莲

我们使用经济订货批量来决定最优的订购量和生产批量。假设需求量是恒定的，而且到货时间是即时的，这样EQQ就可以作为成本最小化的订货量的近似值。

事实上，任何一个时间段内的需求量都是不确定的。当需求是随机时，自然会产生一个问题；库存低到什么水平时才需求下订单呢？我们把需要订货时的库存量称为订货点。很显然，订货点越高，缺货成本降低，存置成本增加。同样，订货点低，缺货成本增加，存置成本降低。其次，很多情况下，主要原材料、燃料的到货时间也是不确定的，即企业进行采购订货时，原材料、燃料并不能在一个精确的时间到达，有的早，有的晚，这也涉及到一个订货提前期的问题，提前期长，缺货成本降低，存置成本增加，提前期短，缺货成本增加，存置成本降低。那么，企业在每周原材料用量和到货时间均不确定的情况下如何控制库存成本呢？蒙特卡罗法为我们提供了这个问题的解决方案。

1 蒙特卡罗模拟法原理

蒙特卡罗模拟法又称随机模拟法，统计试验法，由匈牙利数学家Von Neumann建立，它是为了求解确定性问题而构造一个与原来问题没有直接关系的概率过程，并利用它产生统计现象的方法，使用这种方法进行模拟时，要从系统的研究方法开始。目前，蒙特卡洛法已成为模拟的有力工具，在物流系统工程中，它被用来解决订货、风险性决策、排队等很多问题。

蒙特卡洛的原理是：在所研究的系统中，采用某种特定方法产生随机数和随机变量，模拟随机事件，对结果进行统计处理，从而得到问题的解。

1.1 注意事项

(1)关于随机数和随机变量的产生。随机数和随机变量的产生必须符合实际问题的概率特征，因此，构造模拟的数学概率模型尤为重要。产生随机数的方法过去常用掷币、袋中摸球等，得到个别具体解之后，把它加以平均，才能获得我们所要知道的决策变量和目标函数之间存在的关系。

(2)关于统计结果的处理。任何模拟问题的个别具体解本身并不表征这个系统。只有得到了很多的个别具体解之后，把它加以平均，才能获得我们所要知道的决策变量和目标函数之间存在的关系。

1.2 蒙特卡洛法的步骤

(1)根据实际问题，对资料进行分析和处理，构造模拟的数学概率模型。

(2)根据数学概率模型的特点，设计和应用降低方差的各种方法，以加快模拟结果的收敛。

(3)给出概率模型中各种不同分布的随机变量的抽样方法。

(4)统计处理模拟的结果，得到问题的解，并估计解的精度。

1.3 随机模拟步骤

(1)求出模拟事件出现的概率。

(2)计算累计频率。

(3)将累计频率转换为随机概率。

(4)从随机数表中任意指定一个随机数作为始点，一个一个地模拟。

2 实例模拟

某企业为改善经营管理降低成本，拟建立主要原材料的经济批量和安全备用量制度，根据过去材料消耗情况得知，耗用量、到货期均不固定。

分析以往资料得知主要原材料在100周内每周的消耗数量(见表1)及100次到货时间统计表(见表2)。

表1 主要原材料每周需用量统计表

表2 主要原材料到货时间统计表

我们知道，蒙特卡洛法的关键是建立模拟模型，而建立模拟的关键是确定随机数，产生随机数的方法有很多，如掷骰子、掷硬币等等，这里我们通过查随机表以确定随机数。为了使用上的方便，人们将预先产生的随机数排列在表格中，称为随机数表(见表3)。随机数表中随机有数的分布具有较好的随机性和均匀性，在取用随机数时要按照随机化性原则确定随机数的起点。随机数的起点确定后，可以从左到右或由上到下连续使用，或按一定间隔使用。

表3 两位数字随机表

成本部门核算该种原材料每周占用成本为10元/件，每批订购量费25元，缺货损失为100元/件。初步确定库存量不足13件时就要订货，订货批量每次16件。用随机数模拟14周的使用、到货、存储量及成本(见表4)，随机数表由表3左对齐横向选用。

表4是按时间顺序进行模拟的，首先从初期存货20件开始。查随机数表得知：第一周需用3件，(表4查到随机数33相当于需用33件)，到第一周末存储数量减至17件，占用成本17×10=170元。第二周也需用3件(随机数50表示需用3件)，第三周随机数为13，需用量为2，第三周末存量减到12件。原设定13件为再订货点，现已低于13件故应订货补充。依此类推可得表4。

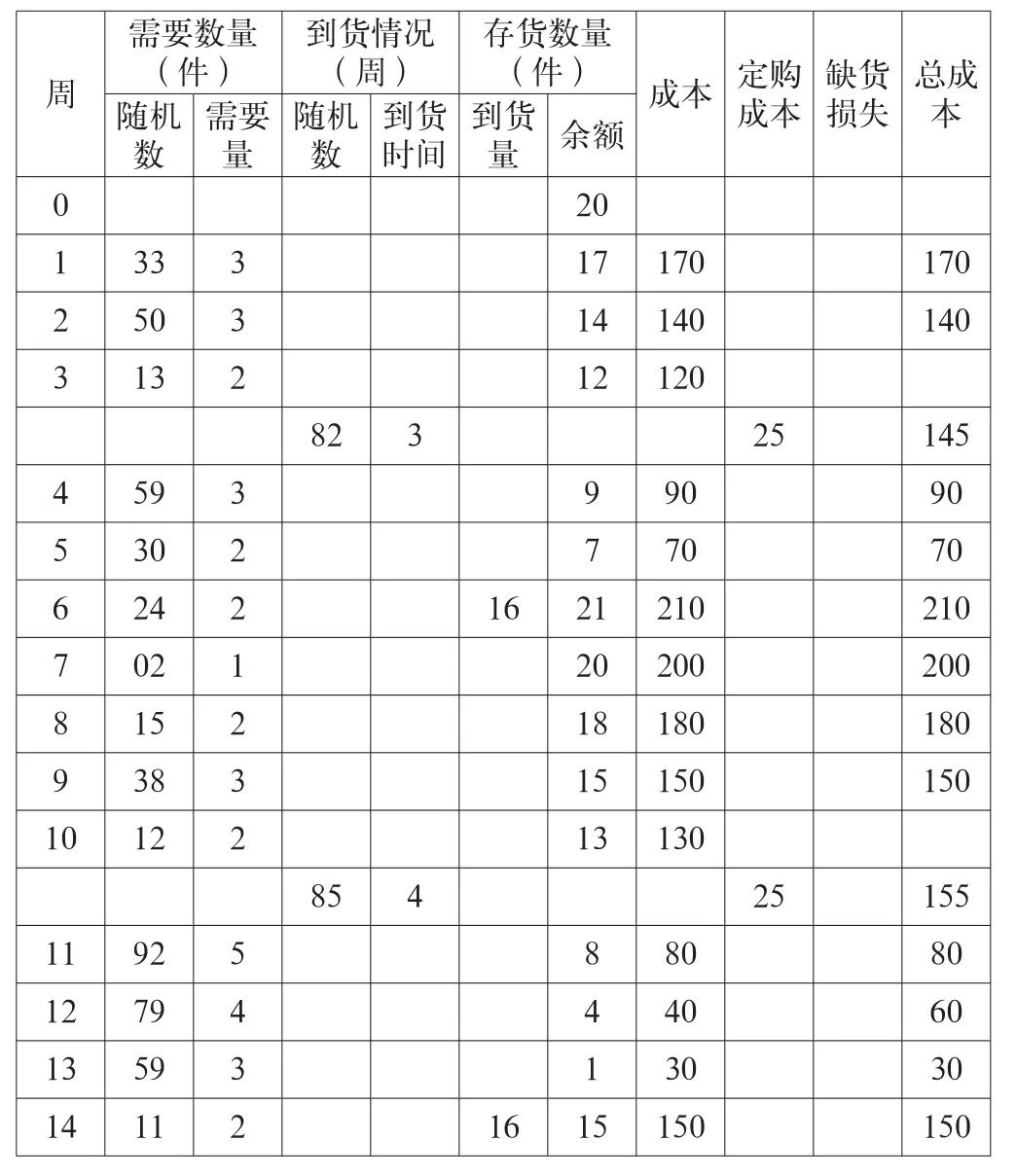
表4 到货、存储量及成本表

通过上表，我们可以看出，需求量是随机变化的，需求量大时，存贮量在单位时间内下降得较快，需求量较小时，存贮量在单位时间内下降得较慢。总共进行了两次进货，第一周期的订货3周内到达，存贮量未降到零时，订货到达，不发生缺货，第二周期四周后到达，也是存贮量未降到零时，订货到达，但面临缺货的危险。

3 结语

表4是订货点为13件，批量为16件，初始存货点为20件的情况，最后得出的平均成本为(170+140+145+……+150)/14=130.7143。如果取不同的订货点，订货量以及初始库存时，可以得到另外的表，可取其中总成本最低做为控制的依据。但真正要计算出库存成本最低时的订货点，订货批量及初始库存，最起码要进行几百次甚至上千次的模拟，现在借助于计算机也可以在很短的时间内完成。

[1]张健中.蒙特卡洛方法[I].数学的实践与认识.