带加劲环埋藏式压力钢管的抗外压稳定性分析
2010-08-06郑林仙陈亚君
周 挺,郑林仙,陈亚君
(1.浙江省水利水电工程局(浙江省水利水电技术咨询中心),浙江杭州 310020;2.浙江省水利水电建筑监理公司,浙江杭州 310020)
0 引 言
在正常情况下,水电站压力钢管可承受高的内水压力,不存在失稳问题,但钢管作为一种薄壳结构,在隧洞放空检修承受外水压力或接缝灌浆承受灌浆压力时,均可能发生压屈而失稳,成为某些工程钢衬设计的控制因素[1-4].伍鹤皋等[2]对埋藏式加劲环压力钢管抗外压稳定的计算方法作了总结,重点讨论了加劲环,对于环间管壁,认为外包混凝土衬砌与钢管之间存在着初始缝隙,使混凝土衬砌对管壁变形的约束作用减弱,故将混凝土衬砌的径向约束作用作为安全储备,相应安全系数略予降低.赖华金等[3]曾提出埋藏式加劲环压力钢管的计算简图并运用壳体稳定理论,推导临界压力pcr的计算公式,但其假定条件较强烈,还得进一步研究.刘东常[4]用半解析有限元法求解加劲环压力钢管外压稳定性问题,目前只能按明管进行稳定分析.林皋[5]按壳体稳定理论建立有限元公式计算锚筋式和加劲环式压力钢管的临界外压,并指出加劲环式压力钢管的临界外压计算公式没有考虑外部混凝土衬砌约束作用,其计算结果是偏保守的.外包混凝土衬砌的径向约束作用必然使钢管的临界外压提高.本文利用通用有限元分析系统ANSYS中的非线性屈曲分析技术,首先对某工程加劲环式压力钢管按明管进行屈曲分析,进而再通过在外包混凝土衬砌和钢衬间设置接触单元按埋管进行屈曲分析,最后与按米赛斯公式和赖华金等所推导的公式(考虑混凝土径向约束)计算的临界外压进行对比,以量化混凝土衬砌径向约束对管壁临界外压的提高,以期为设计人员提供参考.
1 非线性有限元屈曲分析基本思路
屈曲分析是一种用于确定结构开始变得不稳定时的临界荷载和屈曲模态的分析技术.ANSYS提供了两种分析结构屈曲荷载的技术:特征值(或线性)屈曲分析和非线性屈曲分析.利用特征值屈曲分析可以了解屈曲形状和预测出屈曲荷载的上限.然而材料的初始缺陷和非线性使得很多实际结构都不是在其理论弹性屈曲强度发生屈曲,非线性屈曲分析则可得到屈曲荷载的下限.
非线性屈曲分析的基本方法是逐步施加一个恒定的荷载增量直到解开始发散为止,即结构开始变得不稳定,此时的荷载即为临界荷载.其它诸如衬始缺陷、塑性、大变形等非线性也可以包括在分析中.通常钢材本身及钢管焊缝处有一些细观上的缺陷,长期运行管壁会产生不同程度的锈蚀和磨损,这些初始缺陷及锈蚀和磨损的存在,均会降低钢管的抗外压能力.国内规范所采用的米赛斯公式中并没有计入材料的初始缺陷,通常的作法是用较大的抗外压稳定安全系数来保障初始缺陷对临界外压的降低.屈曲分析时可先做特征值屈曲分析求出单位荷载下的屈曲失稳模态,将第一阶屈曲失稳模态乘以一定的因子(如1%)[6-7],并在非线性屈曲分析之前引入作为初始缺陷.
是否发生屈曲最直接的判定可通过计算是否发散加以判断.本文根据屈曲的定义,当外压荷载逐渐增加到一定值后,尽管也许总的变形较小,但荷载再有微小的增加则管壁的变形急剧增加,类似于薄壳的管壁产生波皱,发生屈曲响应.所以本文通过管壁节点的变形——外压荷载曲线的拐点来判断管壁是否屈曲以及屈曲时的临界外压.
2 加劲环式压力钢管按明管非线性屈曲分析
某水电站埋藏式加劲环压力钢管几何尺寸为:管内径r=2100 mm,管壁厚t=21 mm,加劲环间距l=2000 mm,加劲环板厚32 mm,加劲环外径2400 mm.沿洞轴线方向在两个相邻加劲环之间的全圆周内的钢衬连同加劲环建立有限元模型,见图1.所用单元为SHELL143塑性薄壳单元,在加劲环所在平面法向约束加劲环的外侧,在洞轴线方向法向约束加劲环圆环面,在两加劲环间的管壁面外侧沿管壁面法向以0.02 MPa为增量施加外压荷载直到管壁发生屈曲.钢材的应力应变关系采用经典的双向性随动强化模型,用双线性来表示,见图2,两个斜率分别为弹性斜率和塑性斜率,遵守VonMises屈服准则.折点表示钢材的屈服强度,钢材为16 MnR,屈服强度为 325 MPa,弹性模量为 206 GPa,泊松比为0.3.本文为和按米赛斯公式计算出的临界外压对比,环间管壁外压按均匀分布.

图1 加劲环式压力钢管有限元网格图
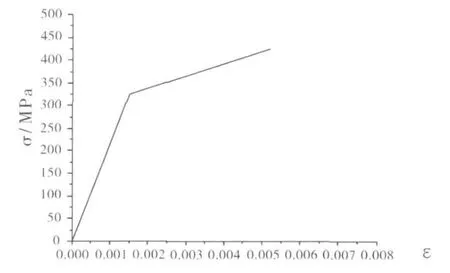
图2 钢衬的应力应变关系曲线
按上所述屈曲失稳的判定,由图3管壁节点变形——外压荷载变化曲线可确定该环间管壁的临界屈曲压力为2.14MPa,当外压荷载超过2.14 MPa时并有微小增加时,管壁则急剧变形发生屈曲失稳.图4是管壁临界屈曲失稳时的变形云图,可以看出管壁发生屈曲时变形的绝对值较小,其值为7.6 mm.管壁屈曲失稳波数为9个,与规范公式计算的波数相同.图5是管壁在临界外压作用下屈曲时的等效应力云图,向管内凹陷的部位超过了钢材的屈服强度(325MPa)而进入塑性,最大应力为337 MPa.
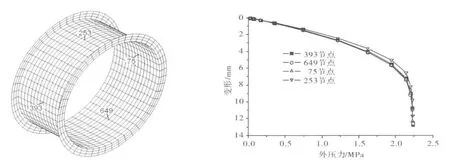
图3 管壁节点变形——外压荷载变化曲线
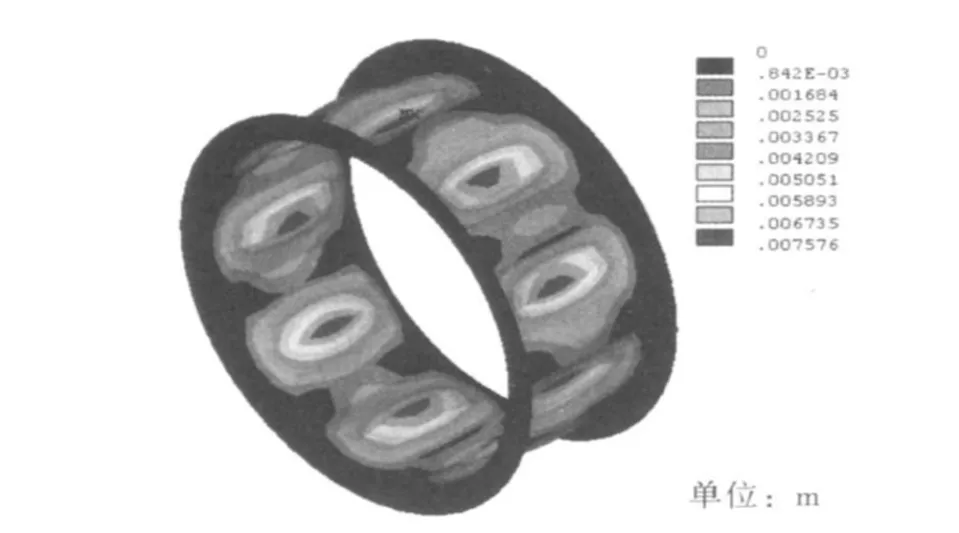
图4 在临界外压下管壁变形云图
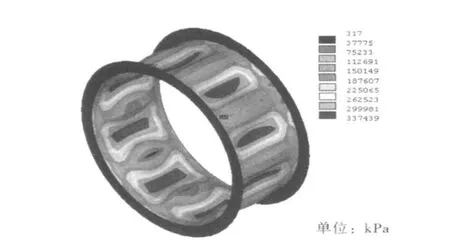
图5 在临界外压下管壁等效应力云图
3 加劲环式压力钢管按埋管非线性屈曲分析
仍以该水电站压力钢管为例,为考虑外包混凝土衬砌的径向约束作用,沿洞轴线方向在两个相邻加劲环之间的全圆周内的钢衬连同加劲环、外包混凝土衬砌和5倍洞径范围的围岩建立有限元模型,在钢衬和混凝土衬砌之间设置接触对(接触单元),并利用接触单元的初始间隙值模拟钢衬与混凝土衬砌之间的初始缝隙,0.8 m厚的C25混凝土衬砌和Ⅲ类围岩均按弹性考虑,有限元局部网格见图6.管周均匀分布的初始间隙值取为1 mm,约束同上,另在加劲环所平面的围岩和混凝土表面也法向约束.在管壁外侧逐级施加外压,每级0.05MPa,随着外压的增加,管壁发生微小的褶皱,有向内凹有向外凸,当外凸变形的管壁与混凝土衬砌接触时则受到混凝土衬砌的径向约束,直到管壁发生屈曲失稳.
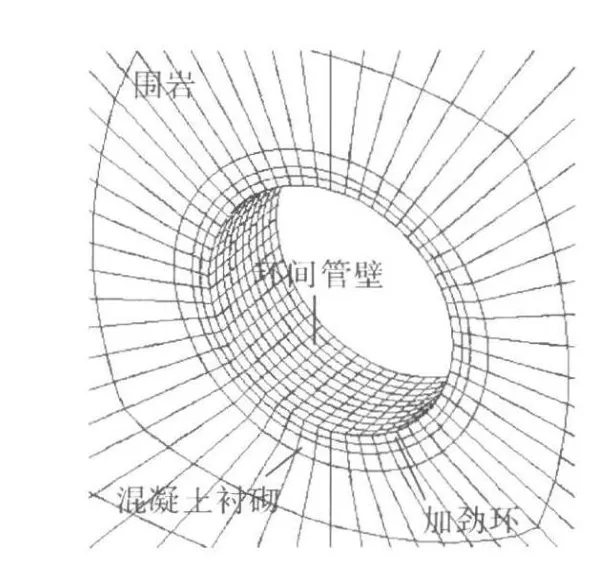
图6 考虑衬砌和围岩有限元局部网格
由图7管壁节点变形——外压荷载变化曲线可确定该环间管壁的临界屈曲压力为3.45 MPa.图8是管壁屈曲失稳时的变形云图,管壁变形的绝对值仍较小,其值为6.7 mm,比按明管屈曲失稳的管壁变形稍小,但屈曲波数则较按明管时多.图9是管壁在临界外压作用下屈曲时的等效应力云图,与按明管屈曲时的管壁应力一致,环间管壁屈曲时向管内凹陷部位的应力为343 MPa,已进入塑性.从变形和应力还可推断,考虑了混凝土衬砌的径向约束后,管壁发生局部屈曲,再引发整体失稳.

图7 管壁节点变形——外压荷载变化曲线

图8 在临界外压下管壁变形云图

图9 在临界外压下管壁等效应力云图
4 不同方法求得临界外压的对比
4.1 米赛斯公式(不考虑混凝土衬砌的径向约束)
规范对设有加劲环的明管和埋藏式加劲环压力钢管环间管壁的径向均布的临界外压值均采用米赛斯公式计算[7]:

式中:pcr—抗外压稳定临界压力计算值,N/mm2;Es—钢材弹性模量,N/mm2;vs—钢材泊松比;r—钢管的内径,mm;t—钢管管壁厚度,mm;l—加劲环间距,mm;n—最小临界压力的波数,由n=2.74(r/l)(r/t)估算,取相近的整数.将各参数代入可得该水电站压力钢管按明管的临界屈曲外压为2.23 MPa.
4.2 赖华金和范崇仁公式(考虑混凝土衬砌的径向约束)
赖华金[3]提出带加劲环的埋藏式压力钢管的计算简图并运用壳体稳定理论,考虑了外包混凝土衬砌对埋藏式压力钢管壁的径向约束作用,求得埋藏式压力钢管的临界荷载.推导临界压力的计算公式如下:

4.3 不同方法下临界屈曲外压对比讨论
从表1不同方法不同情况下的压力钢管临界屈曲外压值可以看出,按明管用非线性屈曲分析计算的管壁临界屈曲外压值由于考虑了初始缺陷和钢材的塑性而比按规范计算值略小.赖华金等[3]推导的公式考虑了外包混凝土衬砌的径向约束作用,没有考虑钢管和混凝土衬砌间的初始缝隙,所以计算出的屈曲临界外压达4.26 MPa,比按明管计算的临界外压值高90%.进一步按埋管用非线性有限元屈曲分析,考虑钢管和混凝土衬砌间的均匀分布的初始缝隙(1 mm)和混凝土衬砌对钢管的径向约束作用,这种径向约束作用使得钢管的屈曲临界外压明显提高,屈曲临界外压从按明管的2.14 MPa增加到按埋管的3.45 MPa,提高了 55%,比按赖华金等[3]推导的公式计算的临界外压降低了20%.

表1 各种计算方法求得该水电站埋藏式加劲环压力钢管屈曲临界外压值
通常认为钢管和混凝土衬砌之间由于各种原因存在缝隙,会减弱混凝土衬砌对钢管的径向约束作用.但明管的屈曲失稳表明管壁向管内凹陷的屈曲波的两侧是向外凸出的屈曲波,波幅相近,尽管管壁临界屈曲时的绝对变形较小,但仍比缝隙大的多,外凸的管壁仍然受到衬砌的约束作用,不会明显减弱.本文对同一尺寸钢管按埋管进行屈曲分析,只是缝隙值从无缝隙到7×10-4r变化,临界外压只减小约10%,但仍比明管的临界外压大50%以上.
以上的分析表明,埋藏式加劲环压力钢管有着较高的屈曲临界外压,规范规定按明管的米赛斯公式计算,将混凝土衬砌的径向约束作用作为安全储备,只将安全系数略予降低,过于保守.在实际施工过程中钢管作为浇筑混凝土衬砌的内模板,加之有接缝灌浆,实际的钢管与外包混凝土衬砌间的初始缝隙呈不连续岛状分布,对比本文按埋管非线性屈曲分析时所考虑的因素,埋藏式加劲环压力钢管实际的屈曲临界外压应介于按本文埋管非线性屈曲分析和按赖华金所推导公式的计算值之间,至少比按明管计算的临界外压提高50%以上.
5 结 语
(1)非线性屈曲分析用一种逐渐增加载荷的非线性静力分析技术来求得使结构开始变得不稳定的临界荷载,以管壁的变形随外压荷载变化曲线的拐点判断管壁屈曲失稳,可用来进行压力钢管按明管或按埋管的抗外压稳定性分析,诸如初始缺陷、塑性、大变形等非线性可包括在分析中.
(2)本文用有限元非线性屈曲分析计算了明管和埋藏式压力钢管的屈曲临界外压,并与规范公式和赖华金、范崇仁所推导的考虑混凝土径向约束的公式计算结果的对比讨论,表明即使混凝土衬砌和钢管间有均匀分布的缝隙,外包混凝土衬砌的径向约束作用也会使环间管壁的临界屈曲外压明显提高,提高幅度可高达50%以上,而实际的压力钢管与外包混凝土衬砌间的初始缝隙呈不连续岛状分布,接触的部位有一定的粘结力,埋藏式加劲压力钢管实际的屈曲临界外压应介于按本文埋管非线性屈曲分析和按赖华金所推导公式的计算值之间.
[1] 潘家铮.压力钢管[M].北京:电力工业出版社,1982.
[2] 伍鹤皋,陈观福,王金龙,等.埋藏式压力钢管抗外压稳定分析[J].武汉水利电力大学学报,1998,31(4):14-17.
[3] 赖华金,范崇仁.带加劲环埋藏式压力钢管外压屈曲的研究[J].水利学报,1990(12):30-36.
[4] 刘东常.半解析有限元法解加劲压力钢管外压稳定性问题的研究[J].水力发电学报,1990(2):41-49.
[5] 林 皋,陈建云,张忠义,等.埋藏式钢管的抗外压稳定研究[J].大连理工大学学报,1998,38(6):700-704.
[6] 博嘉科技编著.有限元分析软件——ANSYS融会与贯通[M].北京:中国水利水电出版社,2002.
[7] 中华人民共和国电力行业标准.DL-T 5141-2001水电站压力钢管设计规范[S].北京:中国电力出版社,2002.
