转子型式对高速透平膨胀机临界转速的影响

赵祥雄 陈双涛 侯 予

1 引言

气体轴承低温透平膨胀机是空分系统和低温系统的关键产冷机械，而且随着基于高速透平逆布雷顿循环的空气制冷技术在航空工业、高速铁路与环境模拟系统中的应用，对高速透平膨胀机的性能和稳定性提出了更高的要求。为了保证膨胀过程具有较高的绝热效率和可靠性，透平膨胀机转子要求具有较高的稳定转速，并最大限度的减小转子系统的振动幅度。如美国目前已经研制出转速高达60万转/分钟的透平膨胀机［1］，中国低温领域工业产品的气体轴承透平膨胀机转速一般也在4万转/分钟以上。工作在高转速下的透平膨胀机其转子结构必须有合理的振动特性才能实现平稳运转，首先要考虑的就是设计转动频率不能与转子本身横向振动的固有频率及其倍数相等或相近。因此进行转子的临界转速特性分析，选取合适的轴承-转子系统型式是高速透平膨胀机结构设计的首要环节。

高速透平膨胀机转子临界转速的计算是转子振动特性分析的核心问题，国内外学者对其都给予了充分的关注。然而，其计算精度、准确性和可行性还有待提高。传统的Prohl递推法和Riccati传递矩阵法在进行转子临界转速计算和振型分析时往往对刚度进行了简化并且忽略了阻尼影响。而文献［2-5］的研究表明支承刚度和阻尼是衡量小型透平膨胀机的气体轴承高速稳定性的重要参数。因此在对微型透平膨胀机转子进行临界转速计算时进行刚度简化和忽略阻尼势必在很大程度上影响计算结果的合理性和精确性。虽然Prohl递推法和Riccati传递矩阵法也有针对各项异性支承且计入阻尼影响的轴承转子系统振动特性进行分析的方法，但是其求解过程十分复杂，不利于程序实现。Nelson，McVaugh等人［6-8］提出的转子系统振动特性的有限元解法在求解具有各项异性支承并且阻尼不可忽略的轴承转子系统时的核心是求解具有形如A x=λB x的广义复特征值问题。其中矩阵A、B均为大型非对称矩阵。而Ward和Moler等人［9-10］提出的求解非对称广义复特征值问题的QZ法是针对此问题一种简便且高效的解法。因此，本文基于有限元划分的QZ法(FEQZ)，求解了具有各项异性支承并且阻尼不可忽略的高速透平膨胀机转子临界转速，经与工程应用结论对比，表明该方法准确度较高，计算简便且行之有效。

2 算法分析

次式为:

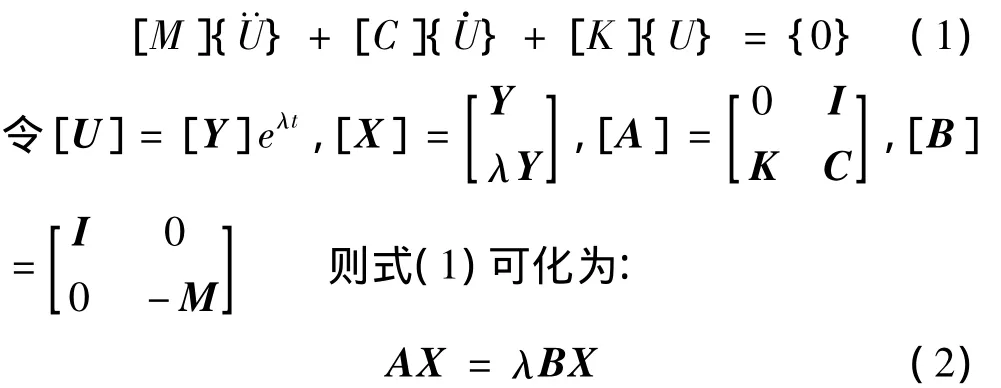
其中:λ的虚部就是转子振动的固有频率。对所得数据进行拟合后联立w=Ω进行求解。

对于转速Ω，其对应的第m阶复特征值λm=sm+jwm，其中s为阻尼系数，w为固有频率，复特征向量

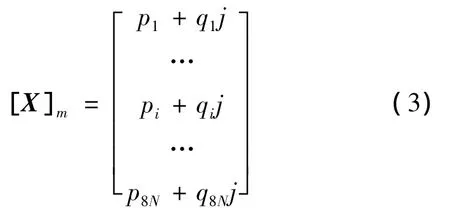
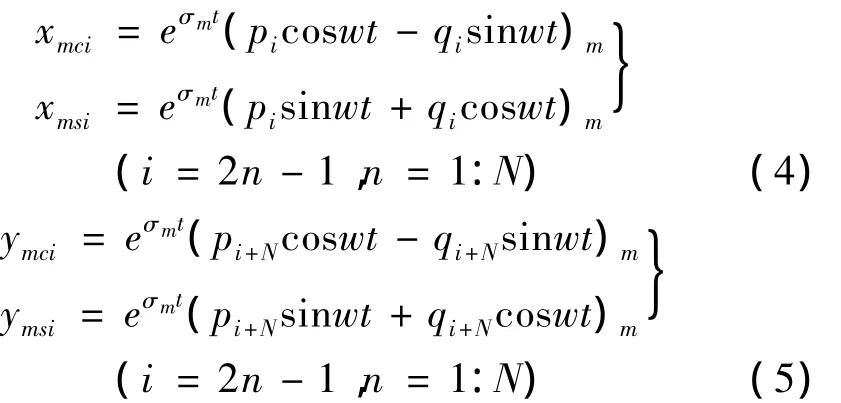
推出的直接用式所求特征向量表示的表达式经简化后可得:

正进动反进动判据:

由此，可以直接用特征向量相关元素来进行正反进动的判别。

用所求特征向量元素表示的某段轴心轨迹方程为:

其中长短半轴分别为:

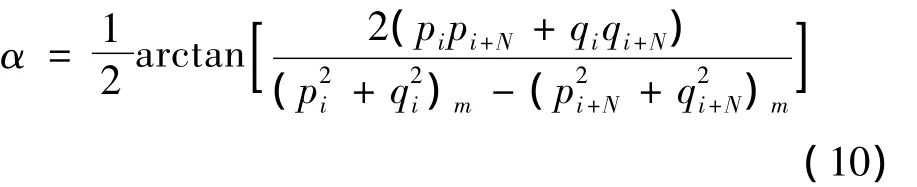
从式(10)可以明显可以看出，衰减指数s＞0时，随着时间的推移，转子最终会出现失稳，s＜0时转子最终趋于稳定，这点十分符合转子动力学中对衰减指数相关性质的描述。对于具有各项异性支承并且考虑阻尼影响的透平膨胀机转子来说，大多数情况下衰减指数s≠0，透平转子涡动的幅值从式(9)可看出是随时间t衰减或者增强的，各个部分的中心轨迹是一系列螺旋线，此时转子的运动十分复杂。根据文献［12］，通常情况下在描述此类节点的运动时令各节点处于稳态，即令式(8)式(9)中的衰减指数s=0所得运动方程作为节点稳态运动方程。

即:

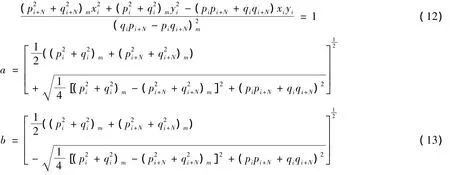
式(13)也能用来做转子正反进动的判别，当b＞0，转子做正进动，b＜0转子做反进动。此外，需要特别提到的一点是，对于支承异性比较严重的转子，会产生混合进动，即一部分节点作正进动，一部分节点作反进动。

3 转子分析实例

为验证算法的正确性，选取在工业上已获得广泛应用的150 m3(O2)/h制氧机用中压低温透平膨胀机 (PLK-8.33 ×2/20-5)为例［13］，其设计参数如表1所示。该低温膨胀机原采用小孔节流切向供气静压气体径向轴承和一体化环形小孔供气静压止推轴承，膨胀机工作轮为反动式叶轮，采用风机制动，双止推盘对置。图1是可供选择的4种转子结构，选定4种结构转子轴的长度相等，采用相同的膨胀机叶轮和制动风机叶轮，采用相同支承条件的气体轴承。计算可知工作轮质量为7.89×10-3kg，极惯性矩5.91×10-7kg·m2，轴惯性矩3.82 ×10-7kg·m2，风机轮质量为2.36 ×10-2kg，极惯性矩4.25 ×10-6kg·m2，轴惯性矩 2.11 ×10-6kg·m2。

表1 透平膨胀机主要设计参数Table 1 Main design parameters of turbo-expander

图1 常用转子型式Fig.1 Four typical rotor structures

3.1 临界转速

表2列出了在各项异性支承下忽略和计入阻尼情况下4种转子前两阶的正进动(F)和反进动(B)临界转速计算值。可以看出，正进动阻尼临界转速低于不考虑阻尼的临界转速，阻尼对一阶临界转速的影响大于其对二阶临界转速的影响。反进动的阻尼临界转速高于不考虑阻尼的临界转速，与正进动类似，阻尼对一阶临界转速的影响较大。实际的膨胀机转子均做正向涡动，对于要求的额定转速，转子1、3、4都符合1.4 wcrn＜ Ω ＜ 0.7 wcrn+1的要求，其中转子4 安全范围最小，转子1转速的安全范围最大。图2是各阶临界转速的Campbell图。由于气膜轴承的各项异性转子的第一阶阻尼临界转速分离为两个临界转速，这与文献［14］描述的油膜轴承各项异性支承的情况类似。

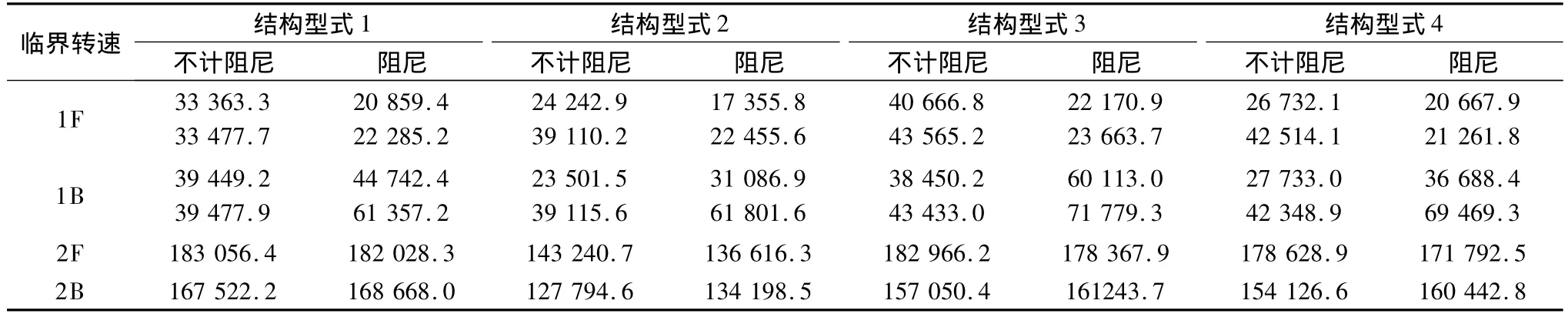
表2 各转子型式临界转速比较Table 2 Comparative on critical speed of four different rotor structures

3.2 振型对比

应用于低温系统的透平膨胀机由于其工作温度较低，尤其是启动过程中的温区跨度和转速变化范围较大。对于设计好的气体轴承支承的透平膨胀机，在未达到额定工作状态前，其刚度和阻尼也会发生变化，特别是动压气体轴承支承的转子，其刚度和阻尼在启动过程中会发生较大变化，这时，如果转子本身对刚度和阻尼的变化比较敏感，则转子的阻尼临界转速和振幅会发生较大变化，反之，转子能够较为平稳的达到指定工作状态。其次还应该考虑两边支承对支承刚度和阻尼敏感度的一致性。

文献［14］指出轴承转子系统某阶复振型在轴承处的幅值越小，则该轴承的刚度、阻尼对该阶特征值的影响越小。图3为4种转子的额定转速下的前两阶复振型曲线。可以看出对于额定转速下的一阶复振型，转子2和转子4的幅值分别在转子左右半边达到最大，转子1和3幅值相差不大，其中转子1幅值最小。从额定转速下的二阶复振型可以明显的看出在转子2支承处的幅值最大，其余转子在支承点的幅值相差较小。针对前两阶复振型，从左右支承的一致性和对刚度和阻尼的敏感度来衡量，转子1和转子3优于转子2和转子4。从图3还可以看出，除了在起始轴段和结尾轴段x方向和y方向的复振幅|X||Y|可以看出有差别外，其余部分几乎重合，这表明转子的振动轨迹在某个平面是接近于圆形的椭圆，这是由于在以上计算中没有考虑转子质心和几何中心的不重合度和支承气膜在x和y方向具有相近的支承刚度所造成的。此外需要注意的是，由于假设s=0，此处的复振幅并不能代表转子实际的振动幅度，它只是转子轴心轨迹的一个形象描述。

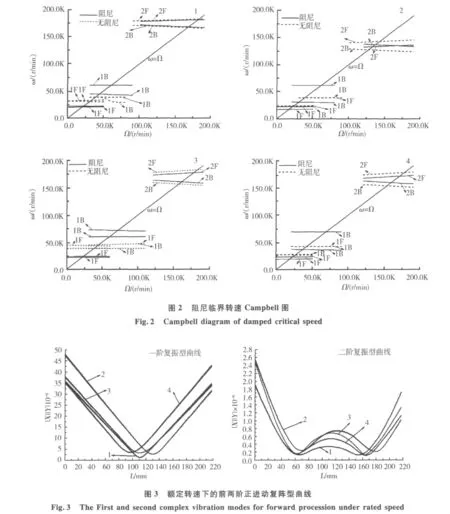
3.3 稳定性分析

用来衡量转子稳定性的无量纲对数衰减率定义为δ=2πσ/w，δ越大表明系统在受扰动后振动衰减的越快，系统的稳定性越好。图4显示了转子1-4前两阶正向涡动固有频率的对数衰减率。从图中可以看出，转子3具有最高的一阶对数衰减率，转子2具有最高的二阶对数衰减率。转子3的二阶对数衰减率大于转子1的一阶对数衰减率。

经过上述分析可知，转子2虽然有较高的二阶对数衰减率，但是其转速安全范围不符合要求，复振动型曲线幅值也较大。转子3有优于转子4的对支承刚度和阻尼的不敏感度和优于转子1的稳定性。综合考虑以上因素，转子3为最佳转子结构。事实上，转子3也是原设计［13］采用的转子形式。

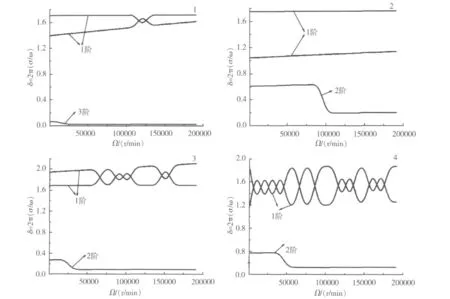
图4 前两阶固有频率对数衰减率Fig.4 The First and second natural frequency logarithm scale attenuation rate

4 结论

通过比较分析，提出基于有限元划分的QZ法是一种简便有效的求解具有各项异性气体轴承支承小型透平膨胀机转子阻尼临界转速简便有效的计算方法，利用QZ法求得的广义复特征向量矩阵，推导出各项异性支承下透平膨胀机转子轴心轨迹的瞬态和稳态表达式，给出了透平转子正反进动阻尼临界转速的两种判据。利用上述方法，对适用于同一透平的四种不同形式转子的阻尼临界转速、复振型、稳定性进行了对比研究，表明采用该算法进行临界转速的计算是十分准确的。并验证了双止推盘对置转子结构具有较好的安全转速范围，并且具有优于单止推盘中置转子结构的稳定性和单止推盘偏置转子对支承刚度和阻尼的不敏感度。

1 陈汝刚，侯 予，陈纯正.微型气浮轴承高速透平膨胀机的研制［J］.西安交通大学学报，2010，44(1):61-65.

2 Zhao H，Hou Y，Chen L，et al.Analytical study of aerodynamic foil bearing with elastic support［J］.Journal of Advanced Mechanical Design.Systems and Manufacturing，2008(2):303-312.

3 Hou Y，Zhu Z H，Chen C Z.Comparative test on two kinds of new compliant foil bearing for small cryogenic turbo-expander［J］.Cryogenics，2004，44:69-72.

4 Xiong L Y，Wu G，Hou Y，et al.Development of aerodynamic foil journal bearings for a high speed cryogenic turboexpander［J］.Cryogenics，1997，37:221-230.

5 Hou Y，Xiong L Y，Chen C Z.Experimental study of a new compliant foil air bearing with elastic support［J］.Tribology Transactions，2004，47:308-311.

6 Nelson H D，McVaugh JM.The dynamics of rotor-bearing systems using finite elements［J］.Journal of Engineering for Industrytrans，ASME，1976，98:593-600.

7 Hashish E，Sankar T S.Finite elment and modal analyses of rotorbearing systems under stochastic loading conditions［J］ .Acoustics Stress and Reliability in Design Trans.，ASME，1984(106):80-89.

8 Childs D W，Graviss K.A noteon critical-speed solutions for finite element-based rotor models［J］.ASME Journal of Mechanical Design，1982，104:412-416.

9 Ward R C.The combination shift QZ algorithm［J］.SIAM Journal on Numerical Analysis，1975(12):835-853.

10 Moler C B，Stewart GW.An algorithmfor generalized matrix eigenvalue problems［J］.SIAM Journal on Numerical Analysis，1973，241-256.

11 钟一锷，何衍宗，王 正，等.转子动力学［M］.北京:机械工业出版社，1987.

12 闻邦椿，顾家柳，夏松波.高等转子动力学［M］.北京:机械工业出版社，1999.8.

13 侯 予，王 瑾，熊联友，等.高速透平气体轴承试验台的建立［J］.润滑与密封，2003，(5):17-19

14 虞 烈，刘 恒.轴承-转子系统动力学［M］.西安:西安交通大学出版社，2001.