锚索的极限抗拔力分析
2010-07-30刘伟平扶名福罗小艳
刘伟平,扶名福,罗小艳
(1.南昌大学 建筑工程学院,南昌 330031;2.江西科技师范学院,南昌 330013)
锚索广泛应用于土木等各类工程中,然而,锚固体与围岩的相互作用的力学问题还不是很清楚,其设计主要还是根据经验。预锚索作用机理的认识也在不断地提高[1-2]。SERRANO A[3]采用 Euler参数方法,假定岩石材料为Hoek Brown强度准则,分析了岩石锚杆的受拉力学性能,根据长细比分成了短锚和长锚。邓宗伟等[4]基于统一强度准则进行了预应力锚索极限承载力计算。本文采用非线性强度包络线,即采用抛物线型和双曲线型 Mohr强度准则[5],并根据极限平衡原理分析了锚索的极限抗拔力。
1 强度包络线形式
1900 年,MOHR提出岩石的破坏发生在岩石内某个面上的剪切破坏,该面上的法向应力σ与剪应力τ满足关系式

但是式(1)并没有明确的解析式,而是根据试验求得。根据直剪试验和三轴试验的结果可知,岩石破坏时应力圆的莫尔包络线是非线性的,即τ与σ呈非线性关系。设破坏包络线为二次抛物线型。
直线型(库仑)强度包强线

φ,c与 σt、σc之间关系为[6]
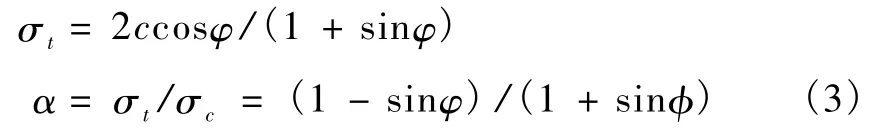
或
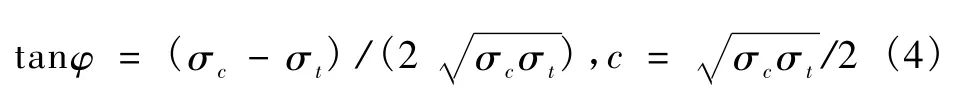
式中,φ为摩擦角,c为黏聚力,α为材料的拉压强度比,σc为材料的单轴抗压强度,σt为材料的单轴抗拉强度。
二次抛物线包络线的一般表达式为[5]
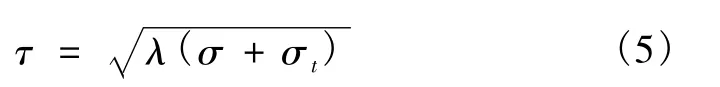
双曲线包络线的一般表达式为[5]

2 锚索极限抗拔力计算
假设锚索锚固段的破裂面为锥体破裂面,如图1所示。在此基础上,采用抛物线型Mohr强度准则和极限平衡原理来研究破裂面上力的平衡,并确定锚索的极限抗拔力。锚索的自由段上的岩土体用超载代替,其大小为q0=γh,其中,γ为自由段上岩土体的平均重度,h为自由段长度。如图1所示,取一微元体进行极限平衡分析,作用在微元破裂面上的切向应力为τ*,法向应力σ*,破裂面的长度设为Δl。
根据文献[7] 破裂面的参数方程为

作用在破裂面上的法向应力σ*计算公式为

式中,k0为侧压力系数,γ′为锚固段岩土体的平均重度,θ为微元体破裂面切线方向与水平向的夹角,L为锚固段长度。
考虑到微元体的竖向力平衡条件,得

图1 锚索极限抗拔力计算模型

略去微分的高阶项并对等式两边取极限,得
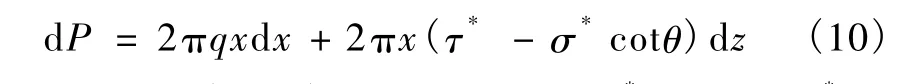
其中,q=γh+ γ′(L - z),cotθ=dx/dz,τ*分别取 τ*=

上述平衡方程可化为

对上式积分,可得出锚索的极限抗拔力计算公式
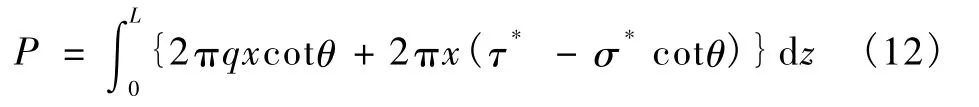
在分析过程中,σ*取灌浆压力与锚固段发生破裂面的围岩压力两者之间的大值。
为计算锚索的极限抗拔承载力,可以利用极值原理来进行求解
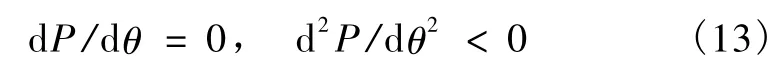
从而找到抗拔力最小时所对应的破裂面,此时的破裂面为真实破裂面,则可确定其极限抗拔力。
3 算例分析
作为算例,假定锚索锚固段长度为5 m,自由段长度为6 m,钻孔直径为100 mm,自由段岩土介质的平均重度γ=20 kN/m3,锚固段的岩体参数指标为:γ′=21 kN/m3,σc=1.85 MPa,σt=280 kPa。图 2 给出了灌浆压力与锚索极限抗拔力之间的关系,随着灌浆压力的增加,极限抗拔力也在增加。这表明,通过合理地增加灌浆压力有利于提高锚索极限抗拔承载能力。通过选用抛物线型、双曲线型和直线型(库仑)强度包络线,得出各自对应的极限抗拔力。从图2可以看出,包络线选取直线型时,极限抗拔力最大,双曲线次之,抛物线对应的抗拔力最小;在灌浆压力较小时,选用不同的强度包络线,对锚索的极限抗拔力影响不大,但当灌浆压力较大时,强度包络线的选取对极限抗抗力的影响加大。

图2 灌浆压力对锚索极限抗拔力的影响
4 结语
1)大多数的岩土材料的强度包络线应该是非线性的,本文基于非线性的强度包络线,即抛物线型、双曲线强度包络线,利用极限平衡原理对预应力锚索的极限抗拔力进行分析研究,并与直线型(库仑)强度包络线进行比较。
2)极限抗拔力受到岩土体的种类、破裂面形状、灌浆压力和围岩压力等的影响。灌浆压力对极限抗拔力有着重要的影响,随着灌浆压力的增加,极限抗拔力相应增加。在实际工程中,通过合理地增加灌浆压力有利于提高锚索极限抗拔承载能力。
3)选用不同的强度包络线,得出的锚索极限抗拔力不同。包络线选取直线型时,极限抗拔力最大,双曲线次之,抛物线对应的抗拔力最小,其结果可以为锚索的工程应用提供理论依据。
[1] 战玉宝,毕宣可,尤春安.预应力锚索锚固段应力分布影响因素分析[J].岩石力学与工程学报,2007,40(6):49-53.
[2] 汪海滨,高波.预应力锚索荷载分布机理原位试验研究[J].岩石力学与工程学报,2005,4(12):2113-2118.
[3] SERRANO A,OLALLA C.Tensile resistance of rock anchors[J]. InternationalJournalofRock Mechanics and Mining Sciences,1999,36(10):449-474.
[4] 邓宗伟,冷伍时,李志勇,等.基于统一强度准则的预应力锚索极限承载力计算[J].岩石力学与工程学报,2007,26(6):1138-1144.
[5] 赵彭年.松散介质力学[M].北京:地震出版社,1995.
[6] 范文,白晓宇,俞茂宏,等.基于统一强度理论的地基极限承载力公式[J]. 岩土力学,2005,26(10):1617-1622.
[7] 何思明,王成华.预应力锚索破坏特性及极限抗拔力研究[J].岩石力学与工程学报,2004,23(17):2966-2971.
