矩形薄板四边固支时的自由振动分析

张 强

(西南交通大学 土木工程学院，成都 610031)

薄板结构在土木工程中应用较为广泛，土木工程结构由于振动特性造成的破裂、损害、倾覆和坍塌等破坏事故已为实践所证实，正确分析与评估土木工程结构在动力作用下的安全性，在土木工程结构的设计中起着十分重要的作用。因此，为了满足工程上各种不同的需要，对薄板振动性能的研究是非常必要的。在一定的横向荷载作用下处于平衡位置的薄板，受到干扰力的作用而偏离这一位置，当干扰力被除去后，薄板在该平衡位置附近作微幅振动。目前对矩形薄板横向振动的固有频率计算方法主要有解析法与数值法，其中数值法有差分法，Reyleigh-Ritz法等。

Matlab软件是一款应用较为广泛的数学软件，在土木工程、机械工程等领域都有所应用。Matlab的基本数据单位是矩阵，它的指令表达式与数学、工程中常用的形式十分相似，故用Matlab来解算问题要比用C，FORTRAN等语言完成相同的事情简捷得多，Matlab软件具有基本的数值运算、矩阵运算、绘制图形等多种功能，特别是Matlab具有十分强大的矩阵运算功能。由于在弹性矩形薄板的有限元分析中会涉及到大量的大型矩阵，所以利用Matlab软件进行弹性矩形薄板的有限元分析较为方便快捷。

1 Reyleigh-Ritz法

Reyleigh-Ritz法即能量法在求解矩形薄板横向振动的固有频率中应用较多。设薄板在平衡位置的挠度为we=we(x，y)，这时薄板所受的横向荷载为 q=q(x，y)，根据薄板的弹性曲面微分方程可得

当薄板以某一频率ω及振形W(x，y)进行自由振动时，它的瞬时挠度可以表示为

薄板自由振动时不受荷载的作用，即q=0，在其自由振动过程中薄板的动能为零时，其形变势能达到最大值 Vε，max

当薄板经过平衡位置时，其自由振动的速度达到最大值，这时薄板的形变势能为零，而动能达到最大值Ek，max

根据能量守恒定理可得到 Vε，max=Ek，max，通过设定薄板的振形函数W，同时满足边界条件即可求得薄板自由振动时的频率。取振形函数为W =(x2－a2)2(y2－b2)2，其可以满足边界条件，根据 Reyleigh-Ritz法可求解出基频ω

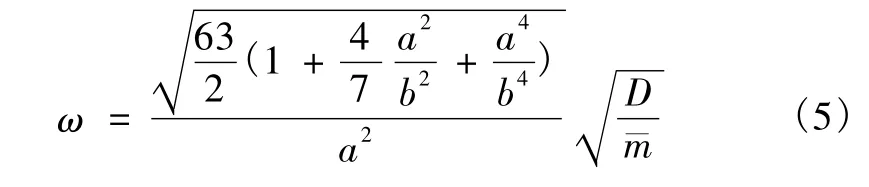
2 基于Matlab的有限元分析

Matlab的具体编程过程可以分为6个步骤，设竖向划分n列，横向划分为m行。划分的网格数越密，计算出的结果越精确。

1)进行单元节点编号:矩形薄板网格划分后总节点数为NN=(n+1)(m+1)，单元节点编号的规律以及单元编号的规律如图1所示，式中NN表示节点总数。

图1 单元与节点编号

2)形成节点位移编号与单元定位向量:对于矩形薄板中面上的每个节点只考虑三个自由度，分别是沿z方向的挠度w，绕 x方向的转角 θx以及绕 y方向的转角 θy;对任一节点，按照 w、θx、θy的顺序进行编写。每个单元对应的四个节点可形成每个单元的定位向量。将单元四个节点按照从左下角逆时针旋转的顺序将其相应的位移编号按照 w、θx、θy的顺序依次列出，即可得到该单元的定位向量。每个单元的单元定位向量是一个1×12的向量。

3)引入边界约束条件:对所有的节点位移清零，将自动形成一个存放所有节点位移的一维数组，其维数为3(m+1)(n+1)。当矩形薄板四边固支时，其沿z方向的挠度w为0，绕y方向的转角θy为0，绕x方向的转角θx也为0，为了方便对组集总刚度的修改，将约束方向的位移赋值为1，而没有约束方向的位移赋值为0。

4)形成单元刚度矩阵与单元质量矩阵。

5)组集总刚度与总的质量矩阵并引入边界条件加以修改:形成单元刚度矩阵与单元质量矩阵后采用对号入座的方法形成总刚度与总质量矩阵，组集完总刚度和总的质量矩阵后，需要根据薄板的边界条件对其进行修改，所使用的方法是主一赋零法。

6)求解开孔板自由振动的频率。

3 计算结果分析

为了验证利用Matlab软件编写的有限元程序的正确性，取弹性矩形薄板a=b=5 m(见图2)，弹性模量E=3.0×1011Pa、泊松比υ=0.3、薄板的厚度t=1 m、薄板的密度ρ=7 900 kg/m3。利用能量法可以得到矩形薄板自由振动时的基频ω=671.33，工程频率f=ω/(2π) =106.85。表1列出了利用编写的Matlab程序计算的基频。

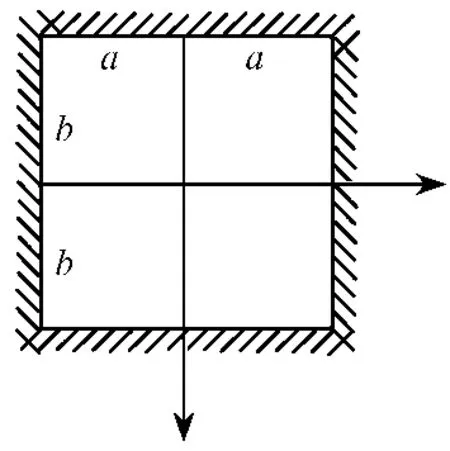
图2 四边固支矩形薄板

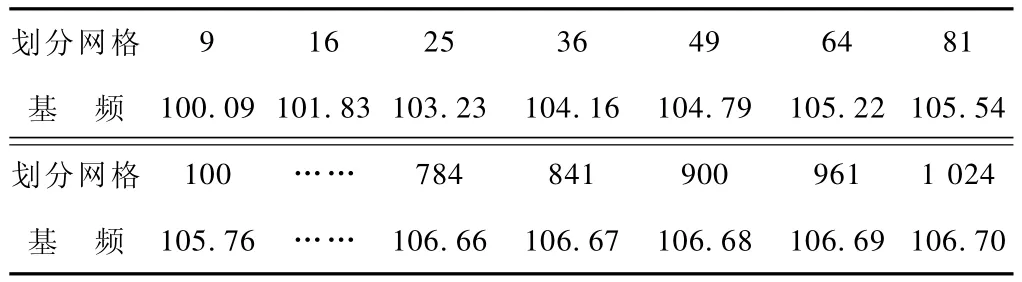
表1 利用Matlab算法求解的基频 Hz

从图3中可以看到，随着网格的不断细分，利用Matlab编写的程序所求解的基频值是收敛的，且越来越接近能量法所求解的基频，表明利用Matlab编写的此算法是合理的，可以应用到其它阶频率的求解中去。

利用ANSYS求解第二、第三、第四阶频率可以得到:

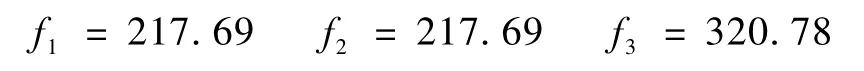
结合表2可以得到利用Matlab求解的频率值与ANSYS求解的频率值相当吻合。且利用Matlab求解中随着网格的细分所求解的频率值越接近于ANSYS求解值，且收敛性较好。

4 结语

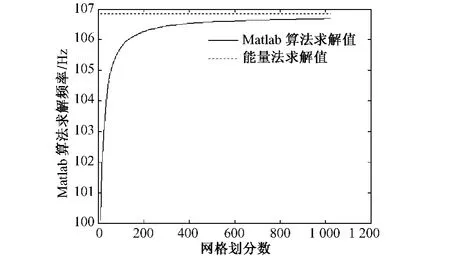
图3 基频收敛性曲线

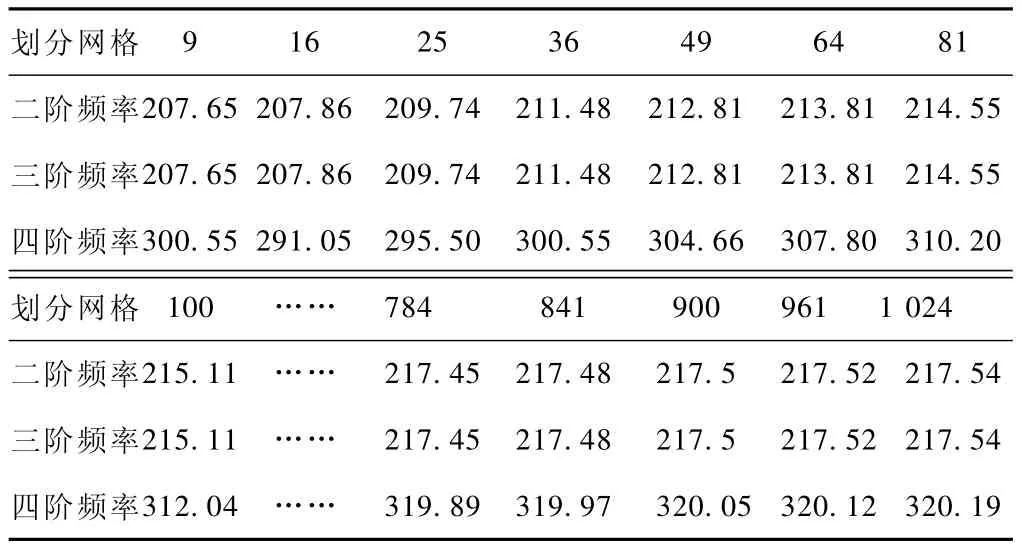
表2 利用Matlab算法求解第二至第四阶频率 Hz

通过比较计算结果说明:基于Matlab软件编写的程序所求解的矩形薄板在四边固支时自由振动的频率值能够达到足够的精度。利用Matlab所画的基频收敛曲线其收敛性较好。因此利用Matlab编写地计算频率程序可以应用到实际工程中去，且能够方便快捷的计算出频率值，具有重要的工程意义。由于在工程实际中，部分薄板是开孔的，因此有待于对开孔薄板进行研究。

[1]杜丽艳.基于Matlab的均布荷载作用下矩形薄板的有限元分析[J].重庆工学院学报，2009(1):32-35.

[2]钟阳，殷建华.两对边固支另两对边自由弹性矩形薄板理论解[J].重庆建筑大学学报，2005(6):29-32.

[3]王道斌，武兰河，李延强.结构矩阵分析原理与程序设计[M].成都:西南交通大学出版社，2006.

[4]徐芝纶.弹性力学(下册)[M].北京:高等教育出版社，2006.

[5]张铮，杨文平，石博强，等.MATLAB程序设计与实例应用[M].北京:中国铁道出版社，2003.

[6]王勖成，邵敏.有限单元法基本原理和数值分析[M].北京:清华大学出版社，1997.