基于图像奇异值分解的滚动轴承故障模式识别
2010-07-26秦海勤徐可君隋育松孟照国
秦海勤,徐可君,隋育松,孟照国
(1.海军航空工程学院 航空机械系,山东 青岛 266041;2.青岛科技大学,山东 青岛 266042)
目前基于故障特征频率的诊断方法[1-3]是滚动轴承常用的诊断手段之一。当滚动轴承发生故障时,不但其特征频率会凸显,而且其振动信号三维和二维谱图中也包含着丰富的故障信息。提取并利用这些谱图信息对于进一步完善轴承故障诊断技术和提高诊断精度具有现实的指导意义。
图像矩阵奇异值能够反映图像的本质特征,把滚动轴承振动信号的S变换三维时频谱图转换为二维灰度图,应用奇异值欧氏距离作为两幅图像相似程度的度量尺度,即可实现滚动轴承的故障诊断。
1 S变换三维和二维谱图的生成
虽然对于振动信号的三维和二维谱图有多种生成方法,如短时Fourier变换、小波变换、Gabor变化、Wigner-Ville变化等。但这些变换均存在一定的固有缺陷,如短时Fourier变换分辨率固定,Wigner-Ville变化存在交叉项等,其应用受到了一定的限制。而由Stockwell提出的S变换不仅吸收了短时Fourier变换和小波变换的优点,而且克服了两者的缺陷,同时也不存在交叉项[4]。S变换通过Gauss窗将短时Fourier变换和小波变换进行了有效的结合,具体定义为:
(1)
(2)
式中:x(t)为能量有限的信号时间序列函数;X(f)为x(t)的Fourier变换;w(t,f)为Gauss窗函数;f为频率;τ为时窗函数的中心点,表示Gauss窗函数在时间轴上的位置。
从S变换的定义可以看出,时窗宽度σ=1/|f|与频率f成反比,具有与小波变换相似的多分辨率特征。在实际应用中,所得到的信号都是采样离散时间序列,因此使用更多的是离散S变化,可直接由连续变化推导出。
设采样间隔为T,采样时间为t,则采样点数为N=t/T。令f→n/NT,τ→kT,则S变化的离散形式可以表示为:
(k,m=0,1,…,N-1;n=1,2,…,N-1)
(3)


以采样时间为x坐标,频率为y坐标,S变换的幅值为z坐标,所得谱图即为振动信号的三维S变换谱图。三维谱图分别向xy平面、xz平面和yz平面投影即可得到振动信号的二维谱图。
2 基于奇异值距离的故障诊断
2.1 图像矩阵的奇异值分解及其特性
设Ap×q是秩为q的实矩阵,则存在两个酉矩阵U和V满足:
A=UΛVT
(4)
式中:U为p×p的矩阵;V为q×q的矩阵;Λ=diag(λ1,λ2,…,λq,0,…,0)且λ1≥λ2≥…≥λi(i=1,2,…,q),则λi就是矩阵Ap×q的奇异值。
由S变换所得的谱图实质为滚动轴承不同故障模式下的处理图像。处理时该图像常常以矩阵的形式表示,因此图像的各种特性以及纹理特征等包含在矩阵元素中。而矩阵的度量特征与奇异值密切相关,故奇异值反映了图像的一种代数本质,这种本质是一种内在属性[5-6]。
由于:‖A‖F=‖UΛVT‖F
=‖U‖F‖Λ‖F‖VT‖F
(5)
式中:F表示范数。因此,图像的能量也完全可以由图像的奇异值表示。同时奇异值还具有一系列良好的特性,主要表现为:
(1)稳定性。对图像噪声、光照条件等引起的灰度变化不敏感。
(2)旋转不变性。表示对原始图像旋转后其奇异值保持不变。
(3)比例不变性。表示对图像进行标准化处理后其奇异值保持不变。
这些良好的特性保证了奇异值代表图像特征具有一定的鲁棒性。
2.2 奇异值距离
由于图像矩阵奇异值能够很好地表示图像特征,因此可直接利用奇异值作为故障特征进行诊断。为了更好地区分不同故障状态,以奇异值欧氏距离作为两幅图像相似程度的度量尺度。
对于任意的向量X=[x1,x2,…,xn]和Y=[y1,y2,…,yn],其欧氏距离定义为:
(6)
若向量X和Y相等,则D(X,Y)=0。若X和Y相差越多,则D(X,Y)越大。
3 实例分析
为了验证该方法在滚动轴承故障诊断中的有效性,以Case Western Reserve University(CWRU)的轴承试验数据为例进行说明[7]。试验所用轴承为SKF的6205-2RS型深沟球轴承。利用电火花加工模拟轴承的内圈故障、外圈故障、钢球故障以及正常情况下的4种模式,轴承故障参数如表1所示。利用加速度传感器进行拾振,采样频率为12 kHz,采样时各故障状态轴承转速均为1 772 r/min。
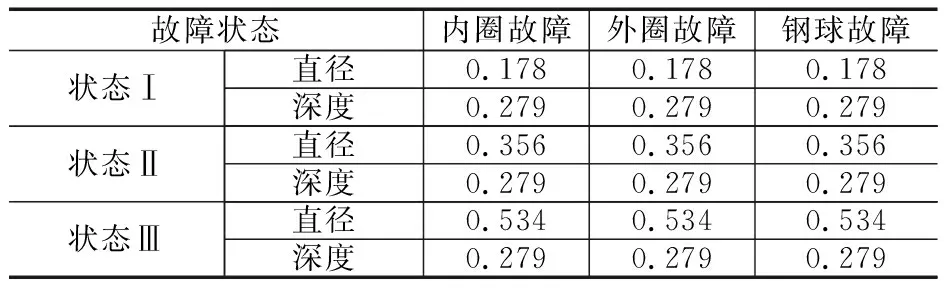
表1 轴承故障参数表 mm
每一故障模式下分别提取25组数据,每组数据长度为2 048个数据点。其中前5组数据用来构造标准故障模式,后20组数据作为测试样本。首先通过S变换求取振动信号的三维时频谱图,图1为状态Ⅱ下4种轴承模式的三维时频谱图。
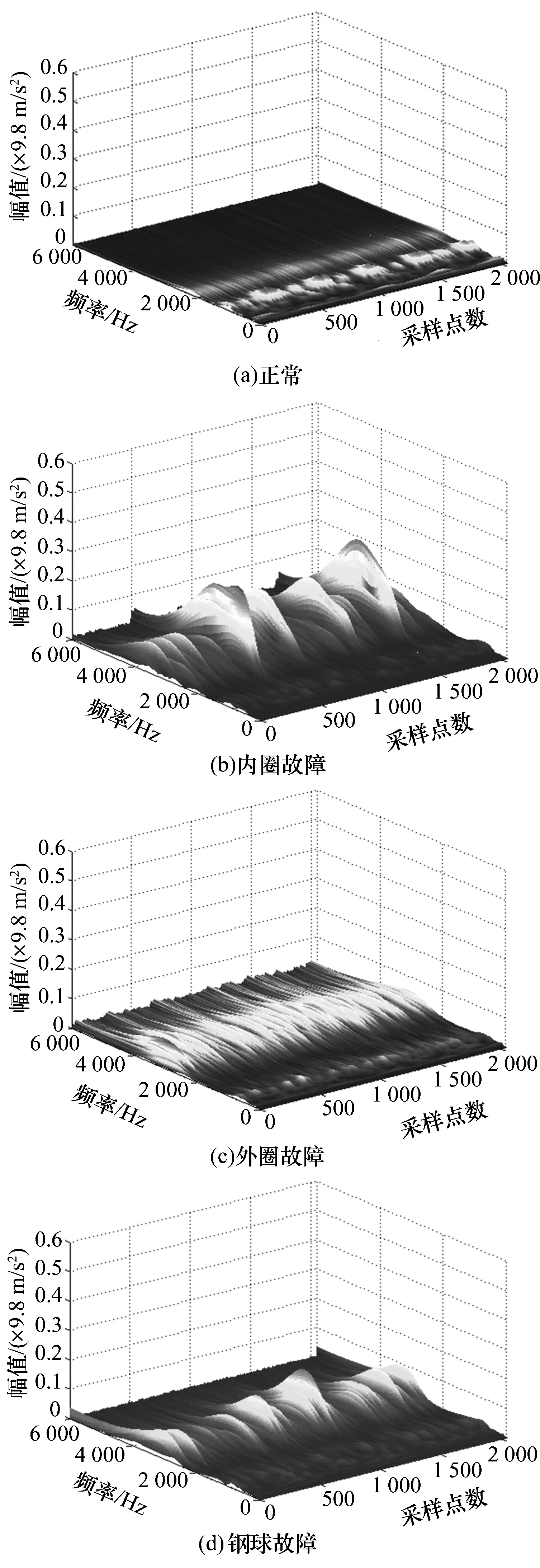
图1 状态Ⅱ下不同模式的三维频谱图
从图中可以看出这4种模式存在明显的差别。在正常状态下信号的能量主要集中在2 kHz以内的低频段;发生内圈故障时信号的能量集中在2~5 kHz;发生外圈故障时信号的能量集中在4 kHz左右且1 kHz附近也分散少许能量;发生钢球故障时能量集中在3~4 kHz。
为了提取图像奇异值特征,需把三维时频谱转换为二维灰度图。在进行转换时既可以向时间频率平面内投影,也可以向频率幅值平面内或时间幅值平面内投影。这3种投影方式各有优缺点,但都舍弃了图像某一维的信息。为了提高故障诊断的精度,应该尽量综合利用这3方面的信息。而三维时频谱本身就是一种三维信息在二维平面的投影,现采用这种投影方式把三维时频谱直接转换为灰度图,图2即为图1经过平滑、滤波处理后的灰度图。

图2 不同模式灰度图
首先,对得到的每一幅灰度图矩阵进行奇异值分解,得到其图像奇异值特征向量。然后,取每一故障模式前5组数据各个图像奇异值特征向量的平均值作为该故障模式的标准特征向量。最后,通过欧氏距离对测试样本特征向量与标准特征向量进行度量即可实现滚动轴承的故障诊断。
取3种状态下每种故障类型各20个样本进行诊断,结果见表2。分析可得,该方法具有较高的诊断精度,尤其在故障尺寸较小时,4种故障都被正确识别出来。但值得注意的是随着故障尺寸的增加,诊断平均正确率反而有所降低。究其原因可能是由于故障的加剧,轴承各部件相互引起的调频效果增强,使得故障特征频率产生相互交叠的可能性大大增强。同时随着故障尺寸的增加,各部件的振动加剧,但由于相互影响有可能使反映在轴承座上的振动在不同故障模式下量值比较接近。正是由于这两方面的原因使得故障加剧时诊断平均正确率反而有所降低。
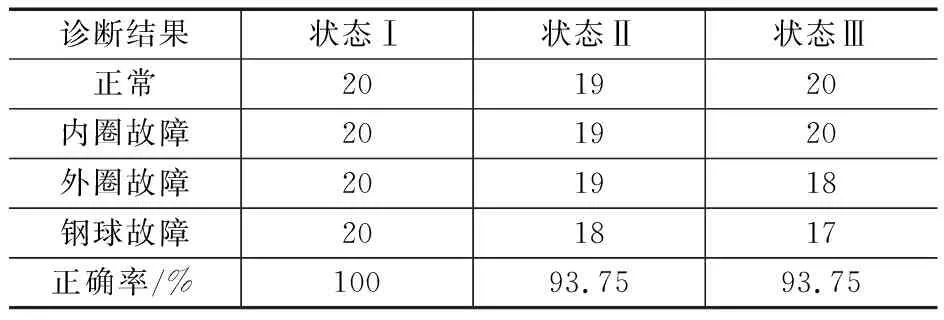
表2 基于图像奇异值特征的诊断结果
为了进一步比较,通过提取各灰度图纹理特征,利用灰关联对各故障状态进行了识别。表3为通过灰关联,利用图像纹理特征对各故障模式的详细识别结果。

表3 基于图像纹理特征的灰关联诊断结果
通过比较表2和表3可以发现。虽然对于个别故障基于图像纹理特征的识别效果好于基于图像奇异值特征向量的识别效果,但绝大多数情况后者优于前者,且后者的平均识别正确率高。进一步说明本文方法的有效性。
4 结束语
对实测不同故障状态数据的分析表明:该方法具有较高的故障模式分类精度,但随着故障尺寸的增加,由于轴承各部件之间的影响,诊断正确率会有所降低。同时,与基于图像纹理特征的灰关联识别结果对比表明,该方法总体识别效果更好。
