基于Origin平台的滚动疲劳寿命Weibull分析
2010-07-26张军利陈建春周井玲
张军利,陈建春,周井玲
(南通大学 机械工程学院,江苏 南通 226007)
滚动接触疲劳寿命具有离散性,需用数理统计的方法处理数据,才能对疲劳性能有比较清楚的了解。在多种分布理论中,由于Weibull分布更接近寿命试验结果,数学处理也较方便,所以在讨论滚动轴承寿命时,绝大多数都采用Weibull分布进行分析[1]。
Weibull分布常用的有图解法和估算法。图解法,即利用Weibull概率纸,对试验数据进行分析和评价。由于使用概率纸比较简单直观,故图解法成为获取Weibull分布参数估计的常用方法。然而,由于受描点、连线、测量的肉眼误差,甚至笔尖粗细等因素的影响,导致这种传统的手工图解法的计算精度不太理想。随着计算机技术的发展,目前已出现了Weibull分布分析的专用软件,如美国的Relex Weibull,Weibull ++等,能较好地解决此类问题。但是,使用此类专用软件进行数据量不大或者频率不高的Weibull分析时,成本相对太高。因此,下文提出了一种基于常用数据分析软件Origin平台进行Weibull分析的简便方法。
1 Weibull分布与Weibull概率纸
1.1 Weibull分布概述
自从Palmgen A将Weibull分布用于滚动轴承分析以来,一直沿用至今[1]。Weibull分布函数为:
(1)
式中:F(L)为轴承寿命不大于L时的破坏概率;L为寿命,作为随机变量处理;L0为分布中最小的寿命值,一般设其为0;β为斜率参数,表示一批轴承寿命的离散性,β值越大,表明离散性越小;η为特征寿命参数,又称作尺度参数,表示破坏概率为0.632时所对应的轴承寿命。文献[2]从疲劳统计理论观点证实了(1)式的合理性。
1.2 Weibull分布概率纸
为便于直观检查Weibull分布与试验结果的符合程度并近似估计Weibull分布的参数,常利用Weibull分布的概率纸[2]。
将(1)式改写成:
(2)
然后,对(2)式两边取两次对数,整理后可得:
lglg[1-F(L)]-1=βlgL+(-lgηβk)
(3)
式中:k=2.303。
设:lglg[1-F(L)]-1=y,β=α,lgL=x,(-lgηβk)=b,则上式可表示为:
y=ax+b
(4)
(4)式为一个线性方程,x,y的关系可用直线在等间隔刻度的直角坐标系中表示。以lglg[1-F(L)]-1为纵坐标刻度,以lgL为横坐标刻度,这样满足(3)式的分布即Weibull分布,在图中为直线,这种格式的纸称为Weibull概率纸[1]。
1.3 Weibull概率纸中寿命数据的标图
将1组寿命试验所得的n个转数数据按数值大小进行排列,可得:L1≤L2≤…≤Li≤Ln,Li称为次序统计量。显然,Li是随机变量,与之所对应的破坏概率为F(Li),F(Li)的数学期望为:
(5)
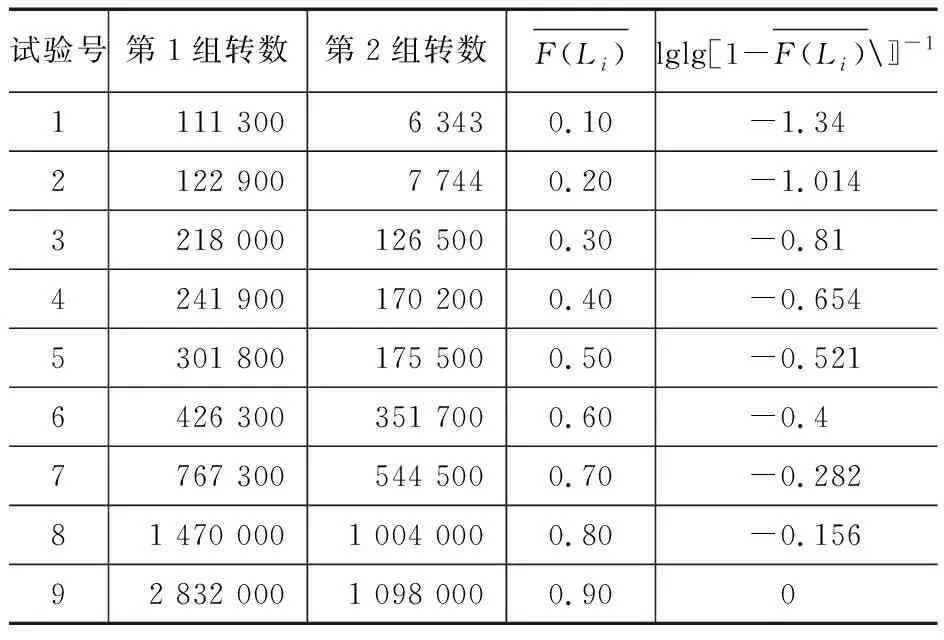
表1 ZrO2陶瓷球疲劳试验数据
2 陶瓷球疲劳寿命的Weibull分布分析
2.1 传统寿命总体估计方法
传统寿命总体估计方法是以手工绘制试验数据点,即在Weibull概率纸上先直接描绘点,然后目测一条直线,读出特征寿命η,当F(L)=90时,则lglg[1-F(L)]-1=0,由(3)式得到的β=lgk/(lgL-lgη)可确定Weibull分布参数,估计寿命。此法虽然简单,但是描点、连线、测量过程中容易产生较大人为误差,使得其计算精度不太理想。当坐标点离散性较大时,还需要应用最小二乘法进行直线回归,即用(6)~(10)式将其变换成等刻度的坐标值x,y后,再进行线性回归[1]。
x=logL
(6)
y=ax+b
(7)
(8)
(9)
F(x)=1-1/1010y
(10)
通过计算 (8)和(9) 式可求得回归直线的斜率和截距,从而得到 (7) 式的表达式,然后用 (10) 式估计总体寿命的分布。从上面的公式和计算步骤可看出,当试验数据组较多时,利用上面的公式进行计算就比较繁琐。
2.2 基于Origin软件平台Weibull分析的方法
下面提出的方法,是在Origin平台上,将试验数据利用最小二乘法原理直接进行直线回归,求得直线的截距和斜率;并且在绘制Weibull概率纸的同时描绘试验点和回归直线。此法方便、易行,且提高了计算精度和工作效率。该方法具体步骤如下:
第1步。将表1第2,3列所示的2组ZrO2陶瓷球疲劳寿命试验数据输入图2的A(x1),C(x2)列,先选中A(x1)列,单击鼠标右键,选中set column values,即出现‘set values’界面,如图1所示,点击选项F(x),选择log(),在窗口中输入式子log(Col(A))。C(x2)与A(x1)操作命令相同,最后按OK自动求得对应的计算结果,如图2中A(x1)和C(x2)所示;图2中B(y1),D(y2)输入表1第5列的数据。
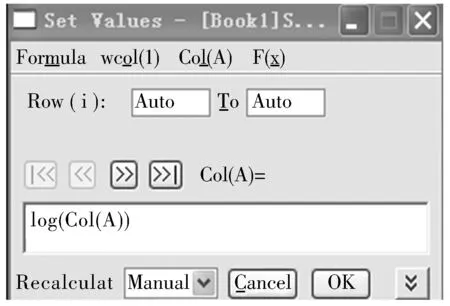
图1 set values窗口中直线的输入

图2 直线拟合所需要的数据
第2步。选中图2的4列数据,使用Origin中菜单栏Analysis>>Fit liner对2组试验数据进行拟合,可分别得到2组回归直线的截距和斜率及相关的其他数据。由图3可知,第1组回归直线的斜率a1=0.841,截距b1=-5.292;第2组线的斜率a2=0.497,截距b2=-3.150。代入(4)式可得回归直线分别为:y1=0.841x-5.292,y2=0.497x-3.150。在Origin中方程的输入与图1相似,第1组输入:0.841log(Col(A))-5.292。第2组输入:0.497log(Col(A))-3.150。
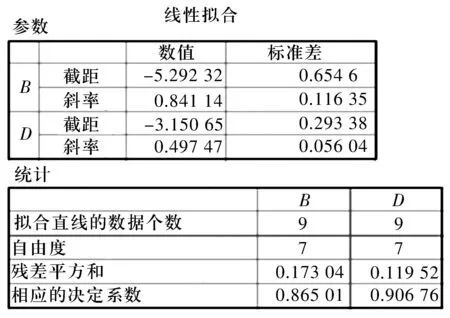
图3 试验点拟合结果
第3步。将用于绘制Weibull概率纸、2组试验点和2组回归直线的数据列在Origin的sheet工作表中,如图4所示。选中sheet工作表中所有数据,点击菜单栏Graph>>Add Plot to Layer>>Line来绘制Weibull概率纸、2组试验点及2组试验点的回归直线。完成直线的绘制后,在Origin的Graph界面中,对横坐标取常用对数,修改线的颜色、线型以及线宽等属性,调整图形后可得到如图5所示的Weibull概率纸、试验点及其回归直线。
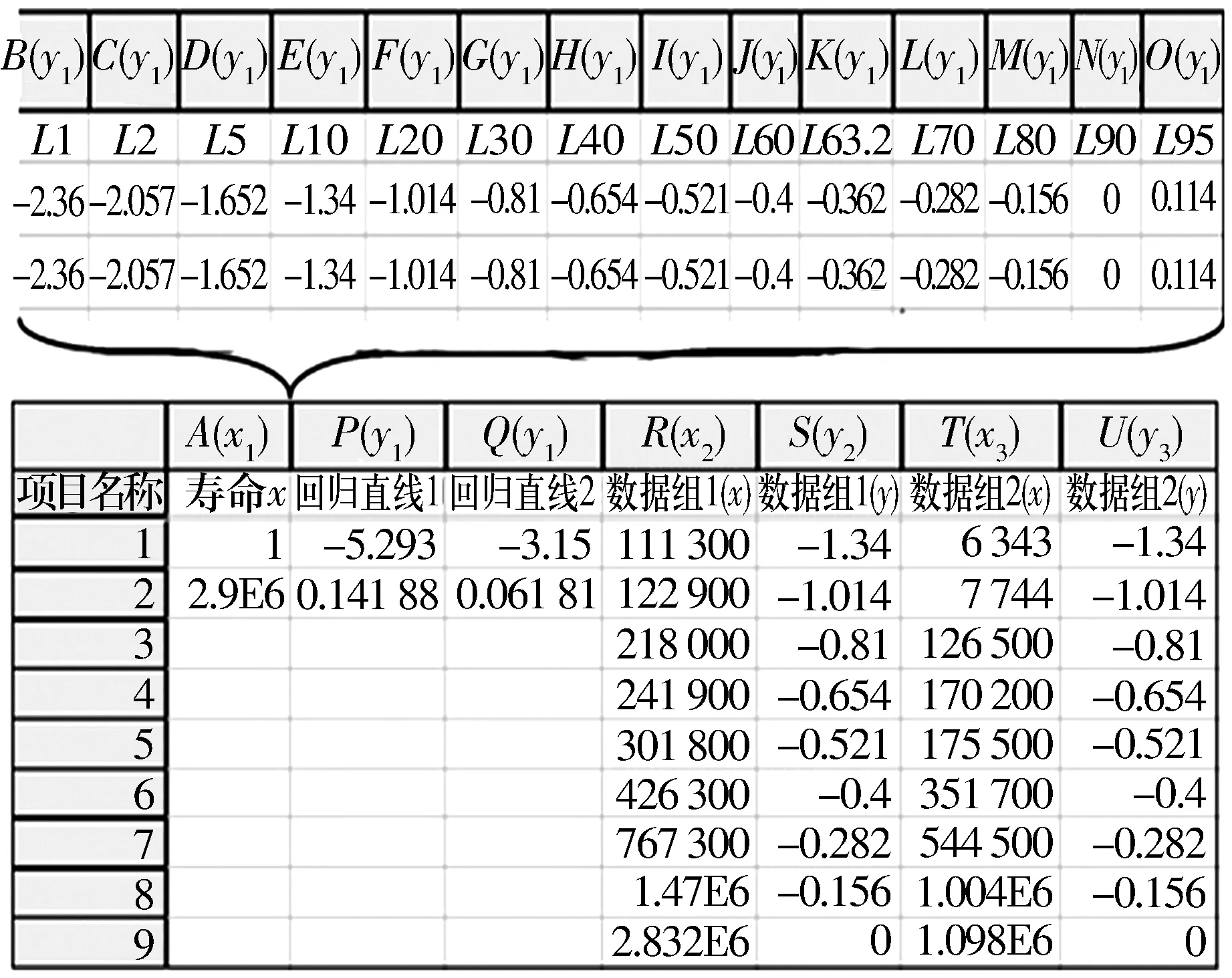
图4 绘制Weibull概率纸和拟合直线所需的数据
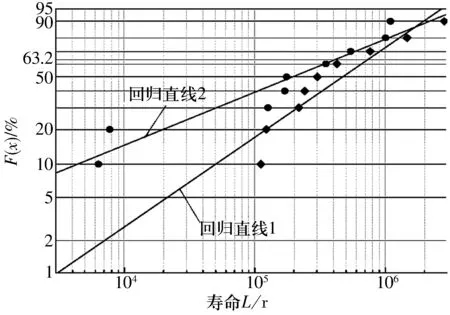
图5 Weibull概率纸上数据的标图
第4步。分析Weibull概率纸上的分布特性。用鼠标选中Origin工具栏中的screen reader或者draw data工具,可在图中读出任意失效概率下的陶瓷球的寿命。如图6所示,第1组试验数据的额定寿命L10=5.016×104,中值寿命L50=4.766×105,特征寿命L63.2=7.363×105;第2组试验数据L10=4.399×103,L50=1.969×105,L63.2=4.079×105。
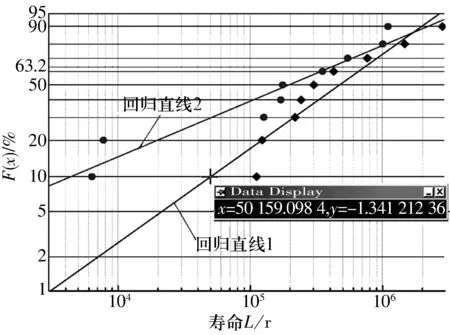
图6 读取任意概率下的寿命值
Weibull概率纸中的每一条回归直线代表1组ZrO2陶瓷球疲劳寿命的概率分布。回归直线在图中的位置反映了该组试验球寿命的长短,直线斜率越小则表示试验球在同样的失效概率下寿命越长。
3 结束语
综上所述,采用基于Origin平台的Weibull分析的方法来绘制Weibull概率纸、试验数据点以及进行直线回归和分析是非常方便的。这种方法减小了传统图解法的误差,弥补了专用分析软件成本昂贵的不足,简化了繁琐的数据计算,为各种试验数据的Weibull分布分析提供了极大的便利。
