基于混沌振子和小波理论的轴承故障诊断方法
2010-07-26纪国宜
张 勇,纪国宜
(南京航空航天大学 振动工程研究所,南京 210016)
混沌振子检测微弱信号主要是利用混沌系统对初始条件的敏感性,当被测信号输入混沌系统后就可导致系统的动力学行为发生变化,从而测出有用特征信号[1-2]。而小波分析是一种多尺度的分析方法,在故障诊断方面有着广泛的应用。现将小波分析思想与混沌振子结合起来检测滚动轴承的故障信号,以实现对轴承故障的成功诊断。
1 基于混沌振子检测信号的方法
1.1 混沌振子方程
从微弱信号的检测下限、混沌系统检测信噪比、系统混沌判据的证明等几方面,文献[3]对Duffing方程进行了改进,提出的混沌检测模型为:
(1)
式中:k为固定值,fcos (t)为周期策动力。此方程构成的非线性动力系统是一个混沌系统,其参数的摄动会引起周期解发生本质的变化。在进行微弱信号检测时,将待检信号作为周期策动力的摄动并入系统,通过观测混沌系统的相轨迹变化,可知待检信号中是否含有周期微弱信号。
设待测信号为:
s(t)=Acos (t)+σrandn(t)
(2)
式中:randn(t)为满足正态分布的均值为零的白噪声;σ为噪声的标准偏差;A为微弱信号的幅值。将s(t)代入(1)式得:
(3)
采用4阶Runge-Kutta法,对(3)式进行数值微分。选择不同的步长时,从同一连续系统中导出的离散系统也不相同,特别是在系统从混沌到有序转变这一特别情况下,不同的步长值将导致分岔值明显不同[4]。考虑到不同的步长h、频率ω以及噪声的强度都会对阈值产生微小的影响,经过大量的仿真试验,认为选取f=0.717较为合适,此时系统虽然处于混沌运动状态,但即将向周期状态转变。
为了满足信号检测的需要,将(3)式进行尺度变换:
ω2[Acosωt+σrandn (t)]
(4)
可以证明(3)式和(4)式系统的分岔值是相同的[5]。
1.2 混沌振子的间歇运动
间歇混沌主要是指非线性系统在时间和空间上表现出的有序和无序交替出现的特殊动力学形态。现所指的间歇混沌是由周期策动力幅值在非平衡相变临界值附近的消涨而引起的。
当内驱动信号与微弱信号存在频率差时:
cos [(1+Δω)t+φ]
(5)
式中:fcos (t)为内驱动信号;Δω为微弱信号与内驱动信号的角频率差;A为微弱信号幅值;φ为微弱信号的相位。对(5)式等号的右侧进行变换,如下所示:
fcos (t)+Acos [(1+Δω)t+φ]=F(t)·
cos [t+θ(t)]
(6)
其中:
(7)
(8)
当Δω≠0时,F(t)在f+A和f-A之间周期性变化。这样混沌系统就出现时而混沌,时而大周期的间歇混沌现象。当Δω很小时,F(t)变化非常缓慢,远远慢于相变过程,因此周期和混沌的出现是泾渭分明的。说明振子相变对小信号很敏感。当系统存在微小角频率差时,F(t)值的大小将在f值左右两侧变化,系统将以ΔT的周期做间歇混沌运动。其ΔT的值为:
ΔT=2π/Δω
(9)
因此可以通过测量ΔT的数值来获得微弱信号频率的数值。文献[4]中应用Duffing振子分析并得出,当角频率差与系统内驱动频率之比不大于0.03时,可以观察到间歇混沌现象的发生。经试验发现,在频差比等于0.03时,微弱信号的幅值要足够大才能较清楚地从图形中看出间歇混沌现象。而在实际中,由于微弱信号幅值都很小,通过仿真得出使用本研究所使用的振子系统在频差比不大于0.02时,应用时域图可以较明显地观测出间歇混沌运动现象。(5)式中令k=0.5,f=0.717,Δω=0.01,A=0.03,φ=-π/6时,系统的间歇混沌运动的现象如图1所示。
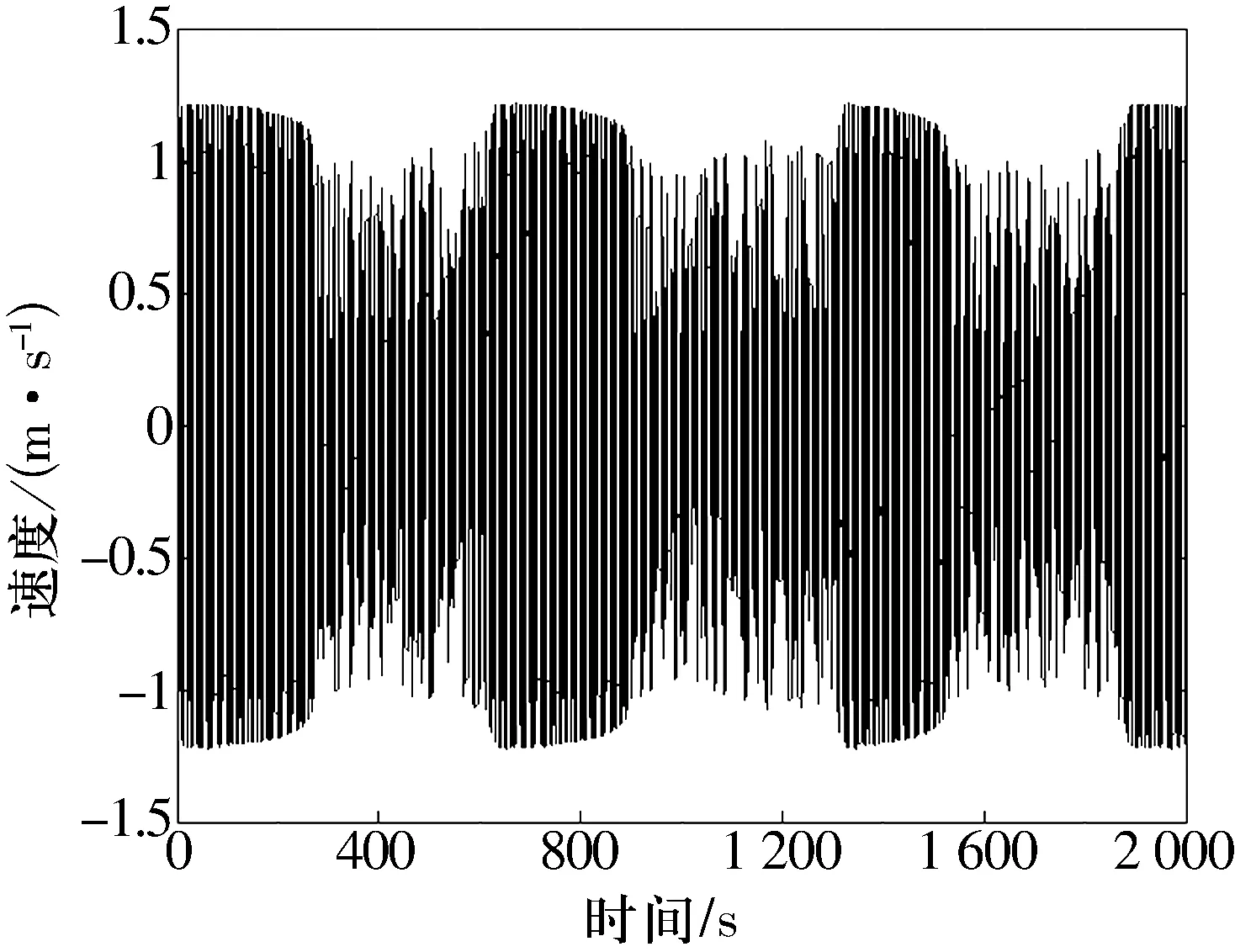
图1 间歇混沌运动状态图
2 滚动轴承故障分析
下面以6205轴承为例,分析其在1 797 r/min下的滚动体故障。轴承损伤采用电火花加工而成,损伤直径为0.711 2 mm,深度为3.810 mm,轴承故障数据的采样频率为12 kHz,轴承各部件的故障频率如表1所示。

表1 轴承各部件的故障频率
小波分析和混沌振子结合检测滚动轴承故障信号的基本原理如图2所示。

图2 检测原理图
滚动体故障的原始数据时域图如图3所示。从表1的轴承故障数据中可以看出,其故障频率点主要集中在低频段,所以在处理数据时采用小波的多分辨率分析原理,应用Daubechies小波对故障原始数据进行6层分解,由于采样频率为12 kHz,故通过小波分解后留下94~187 Hz频率的数据作为分析对象,其时域图如图4所示。再将分解后的信号输入到混沌振子系统进行频率成分的识别。由于故障信号比较微弱(阈值为0.717),为了便于观测,在输入混沌振子系统前可将小波处理后的故障信号适当放大。在混沌振子系统的内驱动频率为140 Hz和144 Hz时,得到了间歇混沌运动现象,如图5和图6所示。
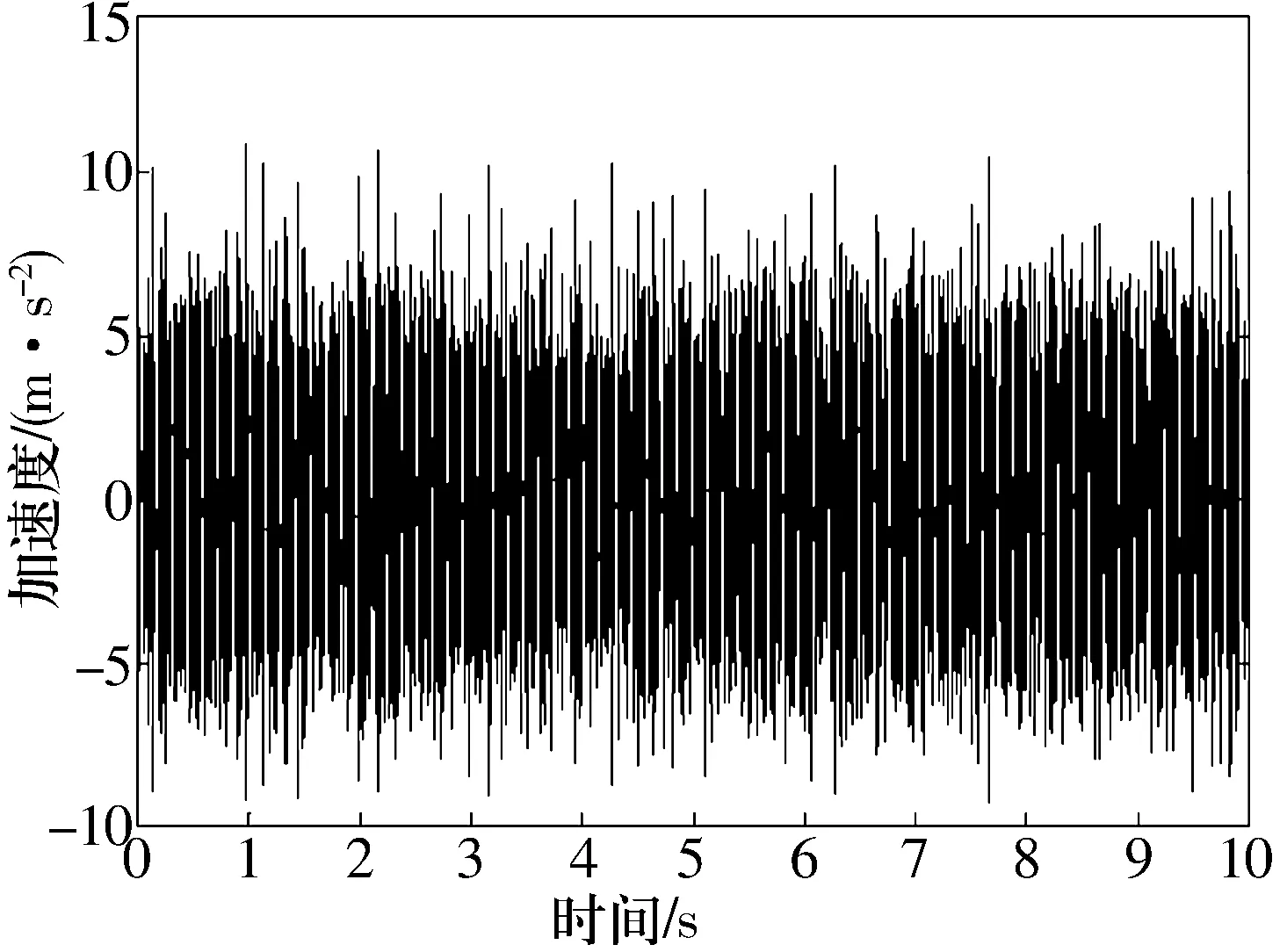
图3 滚动体故障的原始数据时域图
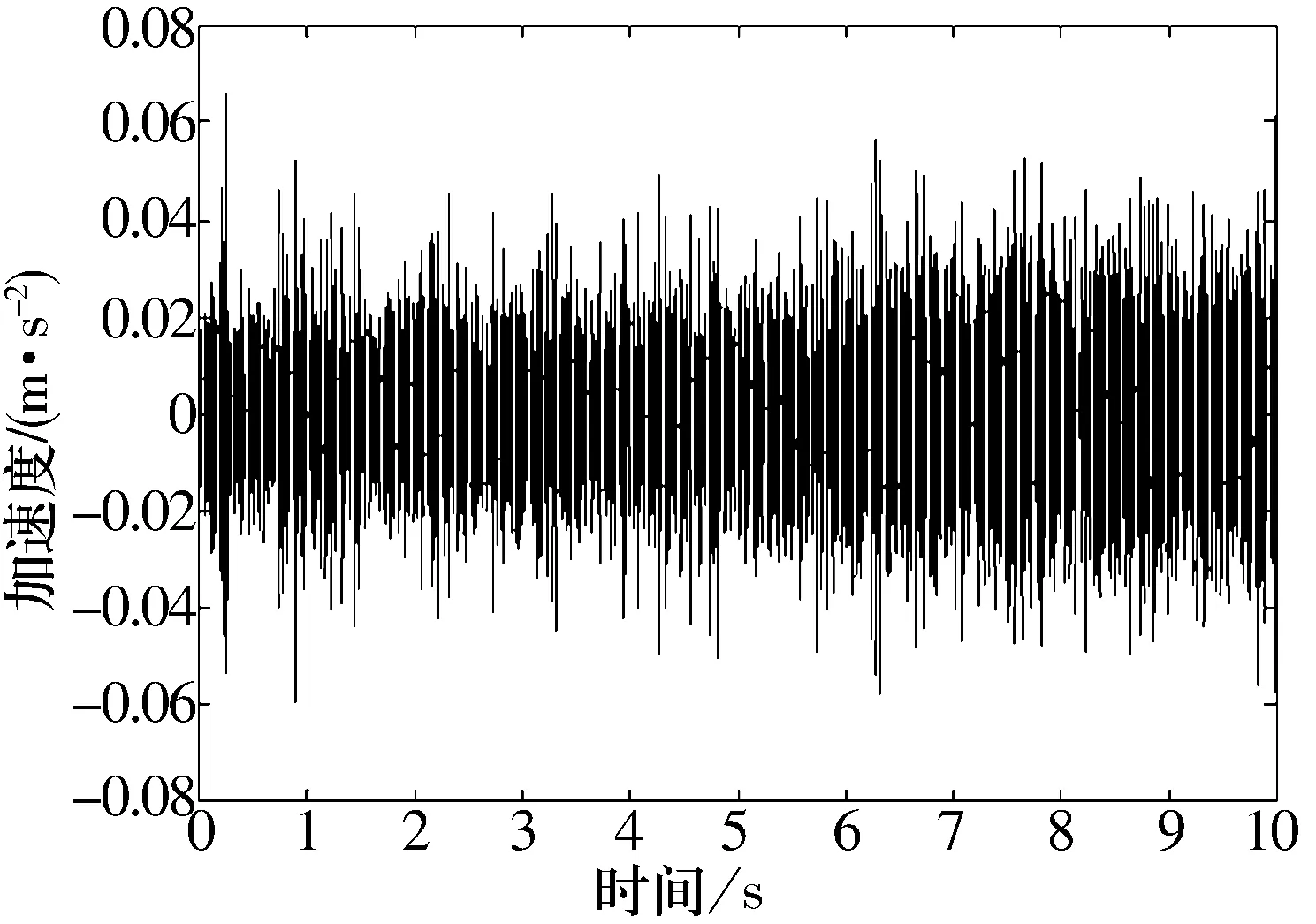
图4 小波分解后时域图
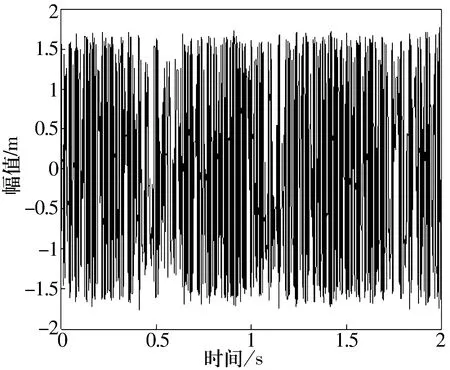
图5 频率140 Hz时的间歇混沌现象图
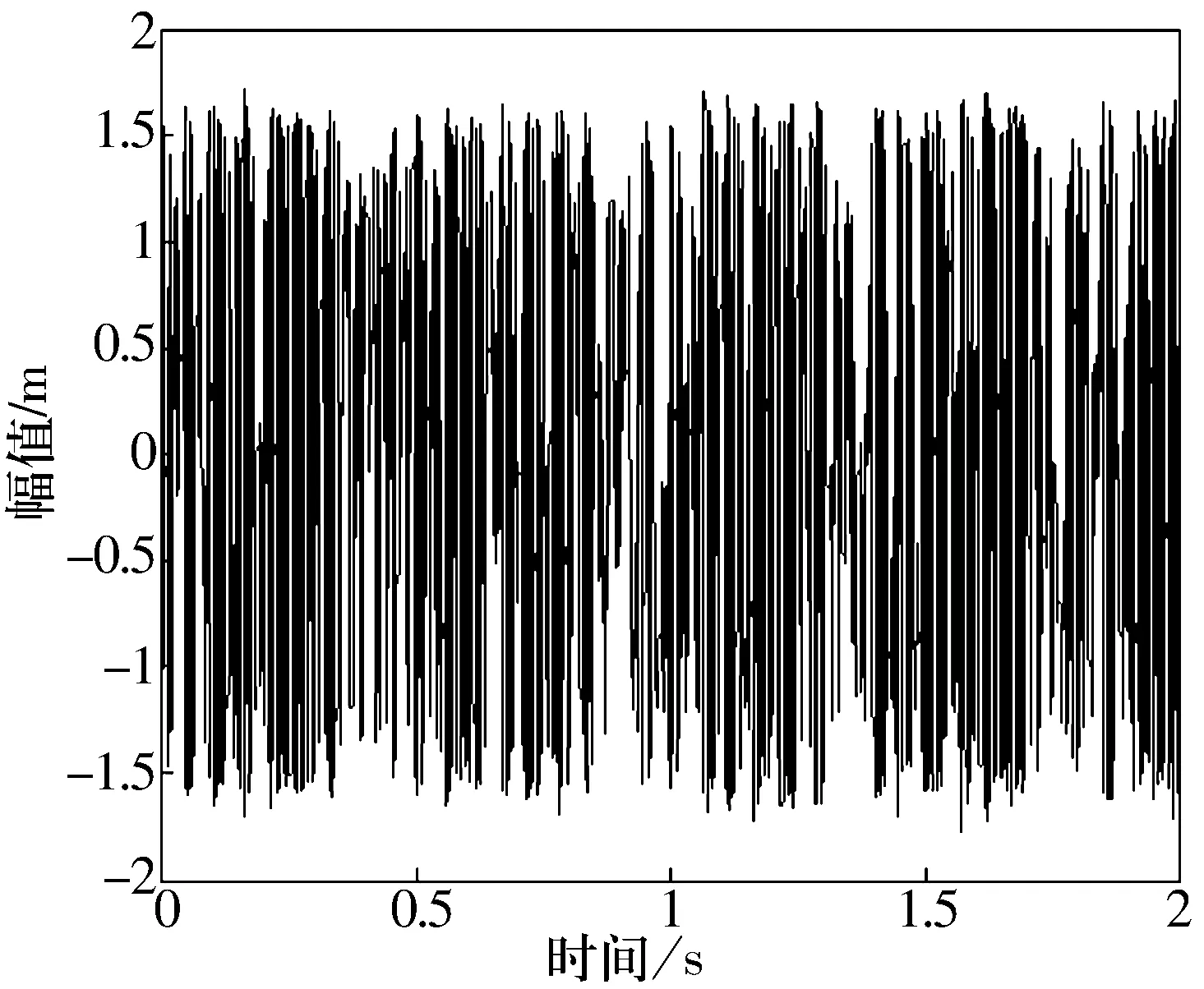
图6 频率144 Hz时的间歇混沌现象图
在频率为f1=140 Hz时,间歇混沌周期ΔT1=0.636 2 s,Δf1=1/ΔT1=1.572 Hz;在频率为f2=144 Hz时,间歇混沌周期ΔT2=0.451 2 s,Δf2=1/ΔT2=2.216 Hz;通过混沌振子系统的间歇混沌运动现象检测到的故障信号的频率大小为:
与理论分析的轴承滚动体故障频率141.17 Hz比较接近,且误差较小。通过以上分析可以判断出此轴承有滚动体故障出现,同时证实了所提出的方法对滚动轴承故障识别具有一定的可行性。
3 结束语
介绍了利用小波分析和混沌振子相结合诊断滚动轴承故障的一种方法,分析了其基本原理及可行性,并通过试验证实了其具有较高的精度和可靠性。该方法具有简单、直观、便于实现的特点,在轴承故障诊断方面具有很好的应用前景。
