基于发电预测的分布式发电能量管理系统

陈昌松 段善旭 殷进军 蔡 涛

（华中科技大学电气与电子工程学院 武汉 430074）

1 引言

由于传统能源资源的枯竭、当今社会许多部门对电能质量要求的提高以及世界各国对环保问题的日益关注，分布式发电系统已经被世界各国所重视[1-4]。但是，分布式发电系统中的部分发电单元，如光伏阵列发出的电能受到气候条件和环境因素的影响[5-8]，具有较强的随机性，因此当其容量达到一定的等级，或者系统中存在储能和其他发电单元时，需要采用一定的能量管理策略对系统的能量流进行监控和管理，优化系统内部各个发电单元、储能单元及其与电网之间的能量流动的方向和幅值，以提高系统运行的稳定性和经济性。当分布式发电系统并网运行时，发电单元发出的电能可以直接供给负荷或者并网，也可存储到储能单元，再由储能单元供给负荷或者并网，电网也可以直接给负荷供电。但是，如何协调发电单元、储能单元、负荷和电网之间的能量流，实现关键负荷优先的可靠供电、发电单元和储能单元的寿命优化、系统运行的经济效益最大化，需要一定的能量管理策略进行能量流的最优控制，保障系统稳定、可靠、经济运行。当分布式发电系统独立运行时，系统脱离电网，系统中只存在发电单元、储能单元和负荷，发电单元发出的能量可直接供给负荷，或者存储到储能单元，再由储能单元供给负荷。由于部分发电单元具有较强的随机性，同时负荷也随着时间处于变化之中，从而在独立运行时分布式发电系统也需要一定的能量管理策略控制系统中的能量流，保持系统内部能量的供需平衡以及电压和频率的稳定性。

目前对于分布式发电系统能量管理技术已有不少研究[9-11]，而这正是分布式发电大规模应用的难点之一。在分析目前分布式发电系统能量管理的研究基础上，本文综合考虑电网实时电价、发电单元预测发电量和储能单元预测剩余容量等因素，提出了一种基于模糊控制的分布式发电能量管理控制算法。该算法能够根据电网实时电价、预测发电量、预测剩余容量和实时运行状态采用模糊规则进行模式切换和能量流的优化控制。文中给出了模拟运行结果，验证了这种算法的良好鲁棒性。

2 系统结构

目前已有系统的网络拓扑主要分为两种，一种是基于直流母线方式，另一种是基于交流母线方式。在基于直流母线方式的分布式发电系统中，风力发电单元和光伏发电单元分别通过 AC/DC变换器和DC/DC变换器与直流母线相连接，这两种变换器均为单向变换器，能量只能从发电单元流向直流母线；多元复合储能单元分别通过AC/DC变换器（如飞轮储能）和DC/DC变换器（如超级电容和蓄电池）与直流母线相连接，这两种变换器均为双向变换器，能量可在储能单元与直流母线之间双向流动。

直流母线方式的系统架构主要优点是：①只需对直流母线电压进行控制，容易满足系统性能要求，控制算法相对容易。②由于省去了子系统中的整流部分，因此系统成本低，易于推广。③采用分布式直流母线控制，系统容易扩展，可以满足用电设备和发电设备增加的要求。直流母线方式系统的关键在于直流母线电压的设定范围和变动方式，从而决定各单元的运行方式。

本文采用直流母线方式的分布式发电系统，其结构如图1所示，由发电单元、储能单元、控制单元和模拟负载单元组成。其中发电单元由风力发电、光伏发电组成；储能单元由铅酸蓄电池组成；控制单元由四个 DC/DC变换器、DC/AC变换器和AC/DC变换器组成。发电单元和储能单元通过相应的功率变换器以直流的形式输出，并汇流到系统的直流母线。直流母线通过独立型DC/AC变换器给关键负荷供电，通过双向DC/DC变换器与储能单元之间进行能量交换，通过双模式型DC/AC变换器与公用电网/配电网之间进行能量交换。

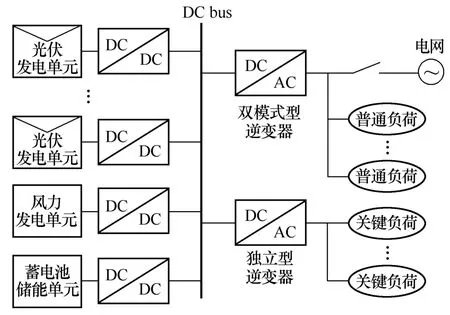
图1 系统结构框图Fig.1 System configuration of distributed generation

3 能量管理

分布式发电系统能量管理的基础是保持系统中能量的供需平衡，即在系统运行过程中的任意时刻均能满足：

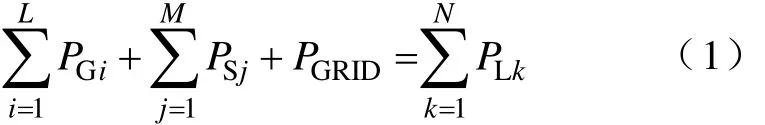
式中，PGi为系统中第i个发电单元发出的功率；L为系统中发电单元的个数；PSj为第j个储能单元吸收或发出的功率；M为系统中储能单元的个数；PLk为第k个负荷需求的功率；N为系统中负荷的个数；PGRID为电网吸收或发出的功率。当系统并网运行即电网存在时，式（1）总能满足。当系统独立运行即电网不存在时，PGRID=0，此时式（1）可简化为

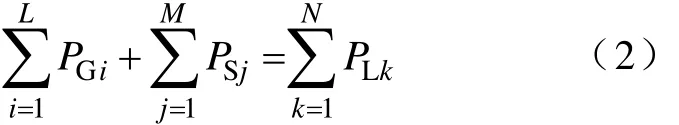
为了使分布式发电系统能够稳定、可靠以及经济地工作，必须保证发电单元和储能单元协调工作，对系统的能量流向进行管理。在独立运行时，分布式发电能量管理控制算法根据发电单元的单位时段运行成本选择运行成本较低的发电单元，优化分布式发电系统的运行成本。在并网运行时，由于分布式发电系统能够实现与电网的电能交换，因此，能量管理控制算法应根据电网电价实时地买入或者卖出电能，追求分布式发电系统的利益最大化。光伏电池和风力发电机等发电单元则将其运行成本与电网电价进行比较，若运行成本高于电网电价时，进入关闭状态；若运行成本低于电网电价时，开始正常启动。对于储能单元，当电网电价最低时，以最大功率给储能单元充电，并可结合电网电价调整充电功率的大小，即电网电价低时，充电功率大，电网电价高时，充电功率小；当电网电价较高时，储能单元根据能量管理系统的调度指令释放足够的电能，在卖电过程中，当储能单元存储的电能释放到只够维持本地关键负荷不间断供电的要求（即备用发电单元启动过程中，关键负荷需要消耗的电能）时停止释放电能，进入待机状态。

3.1 发电预测模块

本文所要研究的分布式发电系统中，发电单元主要由光伏阵列构成，储能单元由蓄电池组构成。为了降低光伏阵列输出电能的随机性对分布式发电系统的影响，能量管理系统需要采取一定的方式先预测光伏发电单元的输出电能，然后依靠预测的输出电能和蓄电池剩余容量制定发电计划，通过分布式发电系统的模拟运行确定变换器及储能装置的实际运行设定值，实际运行过程中再根据发电单元和储能单元的实时状态实时调整能量流传输的大小和方向，使其工作在理想工作模态，从而对整个系统进行能量流动管理，实现负荷需求与发电的能量平衡和系统运行成本最优化。

本文以华中科技大学新能源研究中心光伏发电实验平台(东经114°，北纬30°)为研究对象，以光伏监控系统数据库的历史发电数据和气象数据为参考。以光伏监控系统数据库中2006年12月19日～25日的日发电量数据为例，如图2所示。

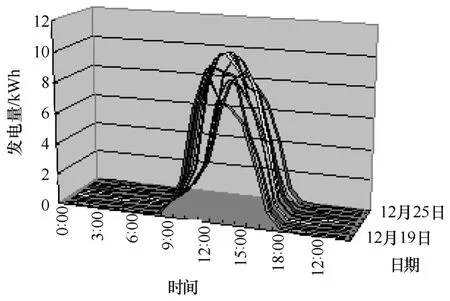
图2 日发电量Fig.2 Daily power output

如图2所示，对于光伏发电单元来说，一个明显的特征就是光伏阵列发电量时间序列的本身高度自相关性。因为在阵列的历史发电量时间序列中，所有的发电量时间序列来自于同一套发电系统，数据自身就包含了光伏阵列的系统信息，解决了光伏阵列的安装位置随机性和光伏阵列的使用时间等对转换效率的影响。除了历史发电量外，还需要考虑日类型、大气温度对光伏阵列发电量的影响。设计的模型结构如图3所示，每个模型的输入矢量为X=（x1,x2,…,x16），其中x1,x2,…,x12分别为预测日前一天的12个时间点的发电量，x13,x14为前一天的最高气温、日类型指数，x15,x16为预测日的最高气温、日类型指数。输出变量y1,y2, …,y12对应预测日的12个时间点的发电量。

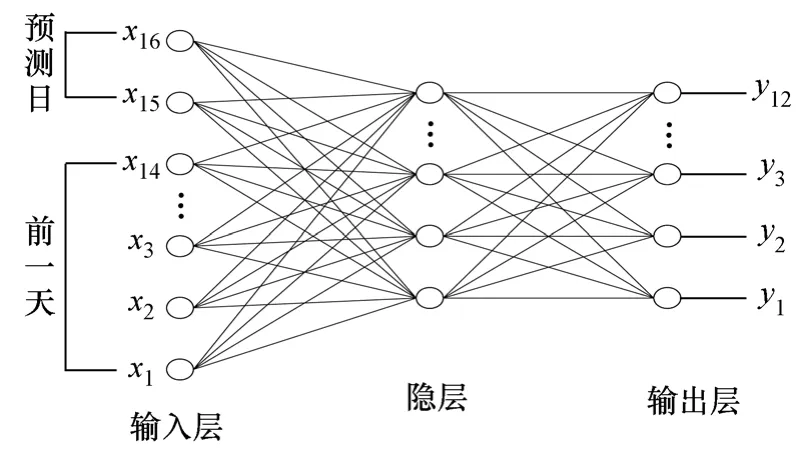
图3 预测模型拓扑结构Fig.3 The topology of the forecasting model

图4为三天皆是晴天时预测模型的预测结果，从图中可以看出，神经网络模型能够准确地预测光伏阵列的发电量。

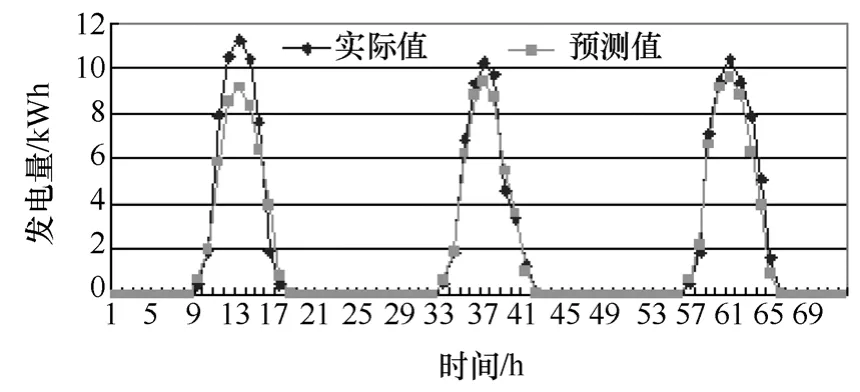
图4 预测模型的预测结果Fig.4 The forecasting results of the model

3.2 最优控制模块

最优控制模块利用数据库中的规则集、当前状态、发电预测模块的预测数据和其他的需求进行推理决策，以确定发电系统的状态转换和控制参数。决策推理模块是能量管理系统的核心模块，它主要由两部分组成：运行模式判断和模糊控制策略。

3.2.1运行模式判断

制定每天的运行模式需要综合考虑光伏阵列的预测发电量、蓄电池组的剩余容量。蓄电池的剩余容量是指在当前工作状态下，蓄电池还能输出的电量。蓄电池的剩余容量也常用其荷电状态来表示。蓄电池能够输出的容量受到许多因素的影响，它不能直接被测量到，同样其剩余容量计算也受到这些因素的影响，也就必须间接计算才能得到。对于这个问题，本文采用安时法进行剩余容量预测。

直接测量蓄电池放电或充电电流，再乘以时间值，就得到安时量。由于充入蓄电池的电量并不都是全部转换成化学能存储，它们之间存在一个充电效率的关系，因此对于充入电量Cch为

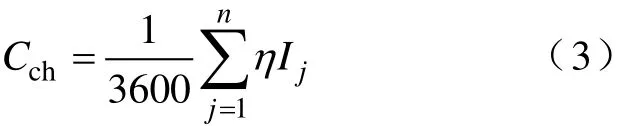
式中，η为充电效率；Ij为第j秒时的充电电流平均值。

由于蓄电池放电深度是影响寿命的一个主要因素，放电深度越大，使用寿命越短。因此，在系统运行过程中，需要考虑蓄电池的充放电管理，保证蓄电池的放电深度情况下兼顾系统运行成本。例如，当蓄电池剩余容量较小，而此后三天的预测发电量小于负荷消耗时，能量管理系统需要采用模式切换在电价较低时增加蓄电池的充电功率，避免在电价较高时由于发电功率不够向电网买电，从而降低运行成本。综合考虑电网实时电价、发电单元预测电能输出和蓄电池的剩余容量，能量管理系统设计了两种运行模式：稳定运行模式和经济运行模式。

运行过程中，能量管理控制算法首先根据光伏阵列三天的预测发电量和蓄电池的剩余容量判断每天的运行模式，然后依靠光伏阵列当天的预测发电量和蓄电池的实时状态查找模糊控制规则进行蓄电池充放电控制器和DC/AC变换器的控制，来实现系统能量管理。在稳定运行模式下，所有时段采用低谷的模糊控制规则，系统优先考虑蓄电池的充、放电管理，保障系统的持续供电能力；在经济运行模式下，不同时段采用不同的模糊控制规则，系统优先考虑系统的运行成本，根据分时电价进行能量调控。具体判断过程见表1。

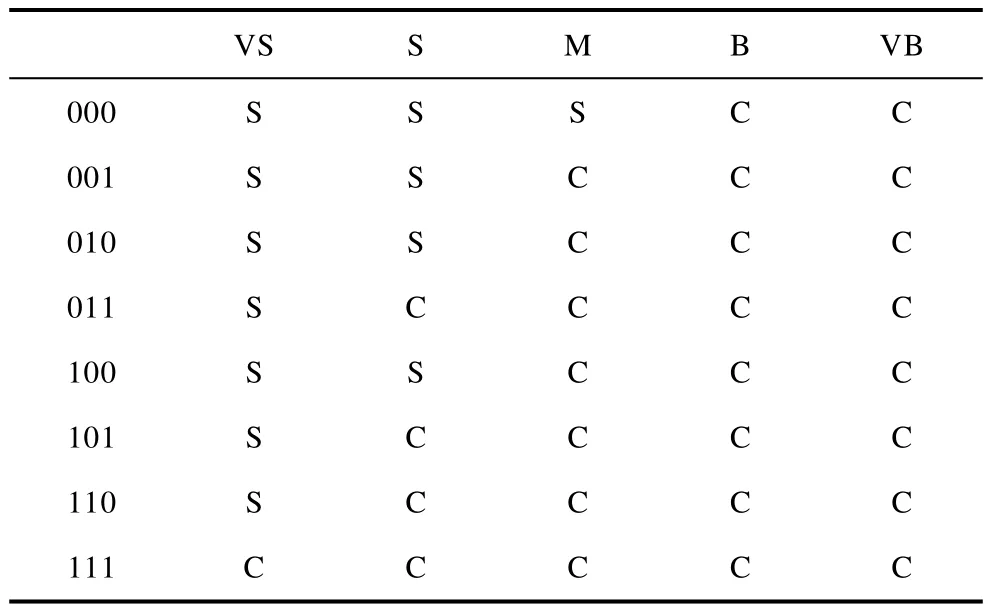
表1 运行模式选择规则Tab.1 Choice rules of operation

表中，S表示稳定运行，C表示经济运行，VS、S、M、B、VB分别表示蓄电池剩余容量为较小、小、中等、大、较大，111表示三天中每天的预测发电量都大于系统额定负荷消耗，001表示三天中只有第三天的预测发电量大于系统额定负荷消耗，其他数字组合的含义可类推。

3.2.2模糊控制策略

模糊控制的最大特征是将人的经验表示成语言控制规则，然后再用这些控制规则去控制系统。因此模糊控制特别适用于模拟人的经验对数学模型未知的、复杂的、非线性系统的控制中。在分布式发电系统中，光伏阵列的发电量预测输出、储能单元蓄电池的剩余容量均为不确定量，所以采用模糊控制进行分布式发电系统的能量管理。模糊控制器采用如下3个模糊变量:

（1）FP（Forecasting Power）——（光伏阵列）预测输出电量。

（2）SOC（State of Charge）——（蓄电池）剩余容量。

（3）DC（Dispersal Current）——（蓄电池）分流量。

其中，FP、SOC为输入模糊变量，DC为输出模糊变量。

把FP论域量化为6档，即:{0 ,1 ,2 ,3 ,4 ,5 }。选用的词集为{0, VS, S, M, B, VB }。把SOC论域量化为11档，即{0 ,1 ,2 ,3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 }。选用的词集为{VS, S, M, B, VB }。把DC论域量化为7档，即: {-3 ,-2 ,-1 ,0 ,1 ,2 ,3 }。选用的词集为{NB,NM, NS, ZE, PS, PM, PB}。FP、SOC、DC的隶属函数分布图如图5所示：

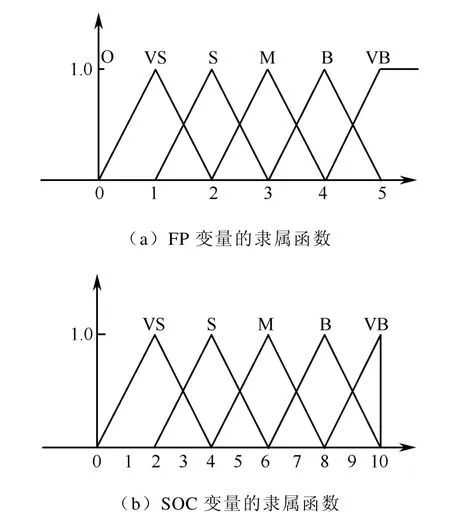
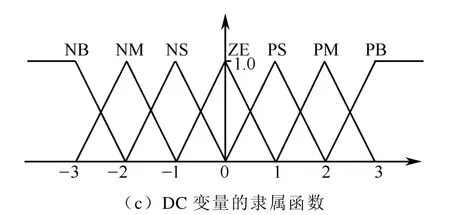
图5 隶属函数Fig.5 Membership functions

分布式发电系统能量管理的目的是系统运行成本最优化，那么在模糊控制规则的制定需要对电网电价进行充分考虑，本文以分时电价为例。其中，峰谷时段划分一般是分为三个时段即高峰、平段、低谷三个时段。高峰为8：00～12：00和18：00～22：00，低谷为 0：00～8：00，平段为 12：00～18：00和 22：00～0：00。峰值电价为 0.6286元/kWh，平段电价为 0.49元/kWh，低谷电价为 0.1050元/kWh[12]。

因此，模糊控制策略为：当运行时间为电价低谷时，系统优先考虑从电网买电提供负载供电和进行蓄电池充电；当运行时间为电价高峰时，系统优先考虑向电网卖电；当运行时间为电价平段时，如果光伏阵列和风机的总输出功率大于负载功率，系统不再优先考虑向电网卖电，而是一边以恒定电流给蓄电池充电，一边将多余的电能卖给电网。具体控制参数见表2。

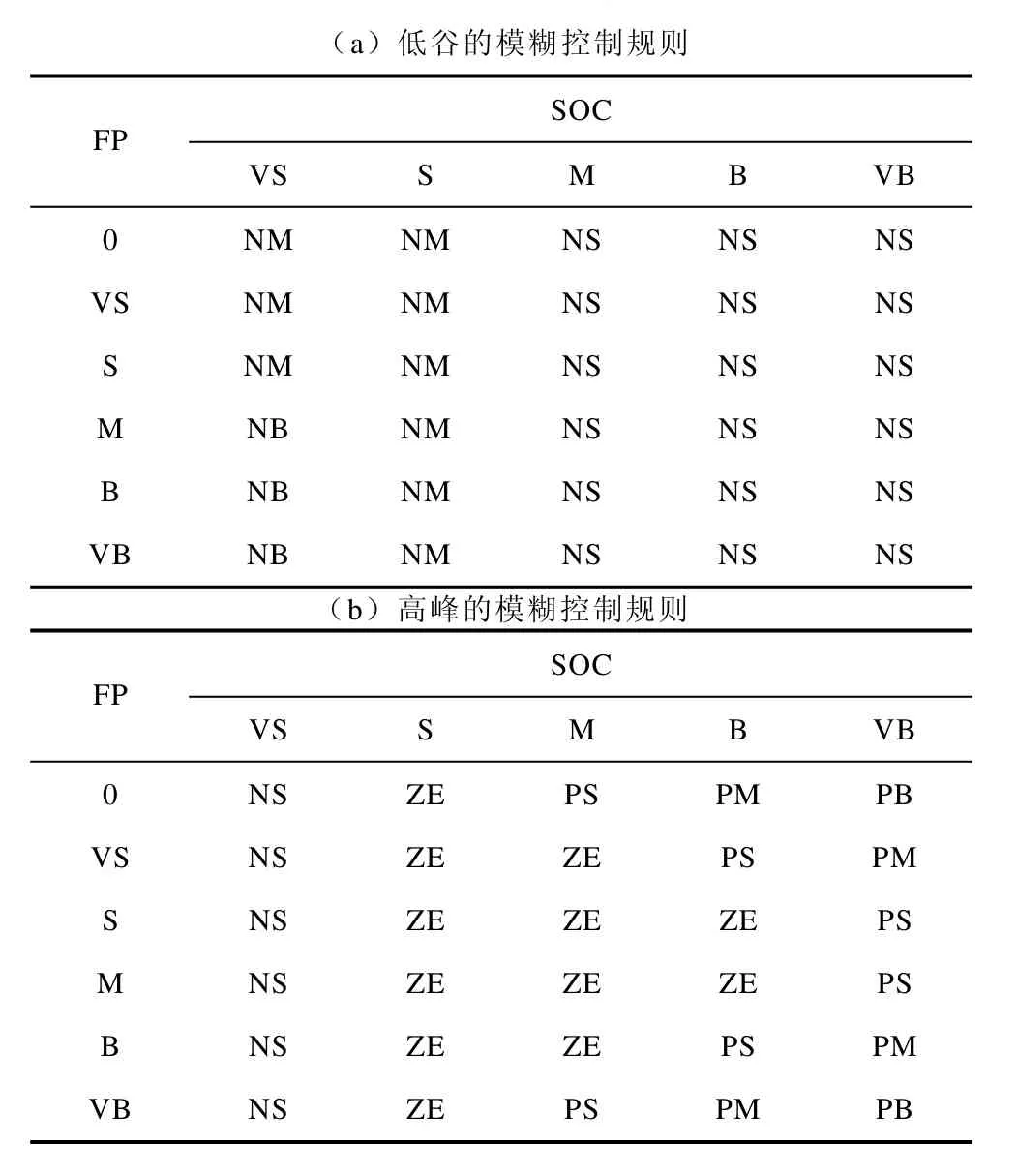
表2 模糊控制规则Tab.2 Rules of fuzzy control

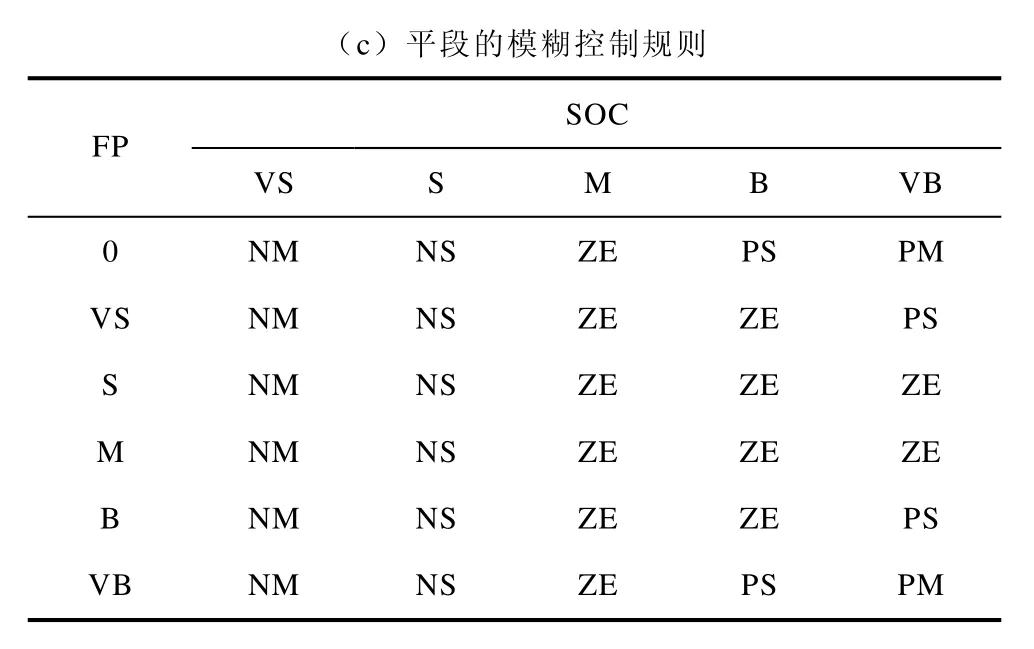
（c）平段的模糊控制规则SOCFP VS S M B VB 0 NM NS ZE PS PMVS NM NS ZE ZE PSS NM NS ZE ZE ZEM NM NS ZE ZE ZEB NM NS ZE ZE PSVB NM NS ZE PS PM

4 算例分析

本文采用组态软件模拟分布式发电系统的运行过程。在考虑气候和地域条件的原则下，分布式发电系统设计为发电单元和本地负荷的容量基本匹配，即在长期运行情况下发电单元的输出电能基本满足本地负荷。模拟运行系统由3.0kW的光伏阵列和1.2kW的风力机组构成发电单元，储能单元由满足负荷需求三天的蓄电池组构成。直流母线通过DC/AC变换器与电网连接实现电能交换，系统模拟运行过程如图6所示。

图6a为系统模拟运行时光伏、风力发电单元的输出功率和负荷需求。图6b为系统由稳定运行模式转经济运行模式。图6c为经济运行模式下的系统模拟运行结果，当运行时间在低谷时，系统从电网买电为负载供电和进行蓄电池充电，电网输出功率为负值；当运行时间为高峰时，系统向电网卖电，电网输出功率为正；当运行时间为平段时，如果光伏阵列和风机的总输出功率大于负载功率，系统一边以恒定电流给蓄电池充电，一边将多余的电能卖给电网，此时蓄电池输出功率为负，电网输出功率为正。表3为系统在图6c的运行过程中与电网买卖的电量及其收益。

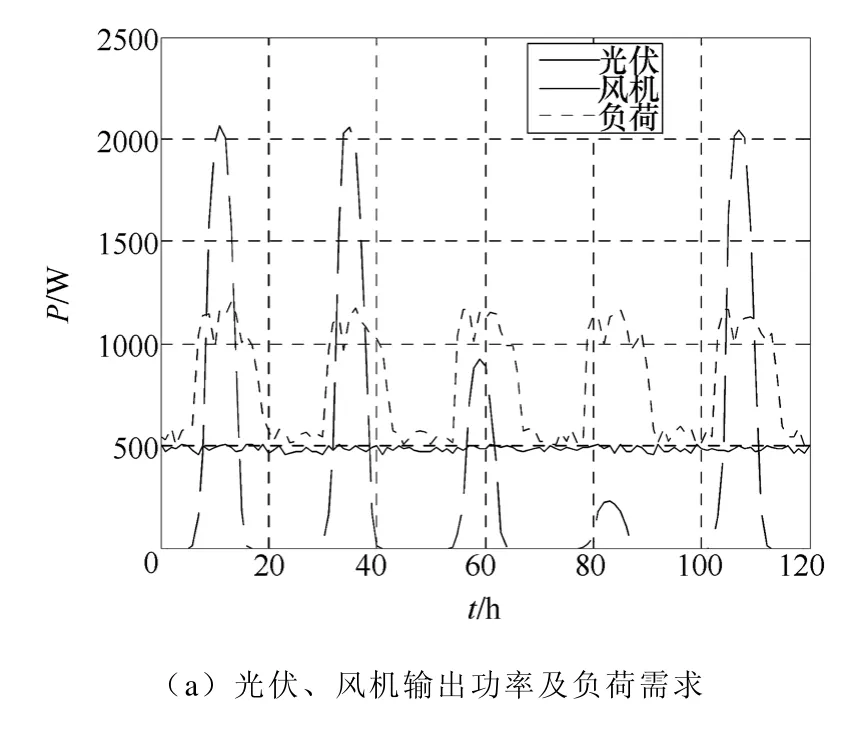
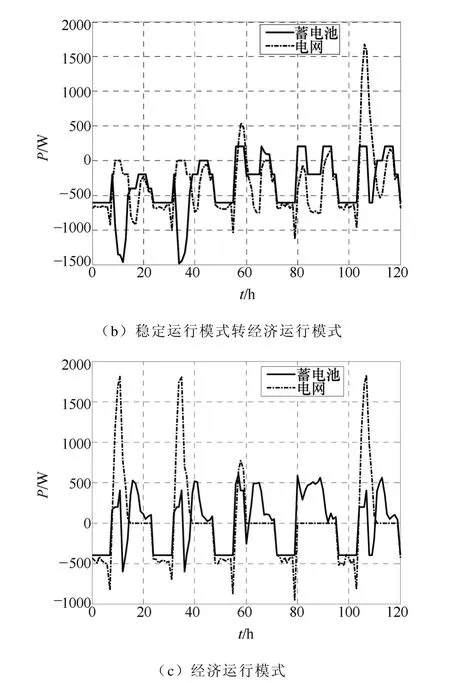
图6 系统模拟运行结果Fig.6 Typical operation results

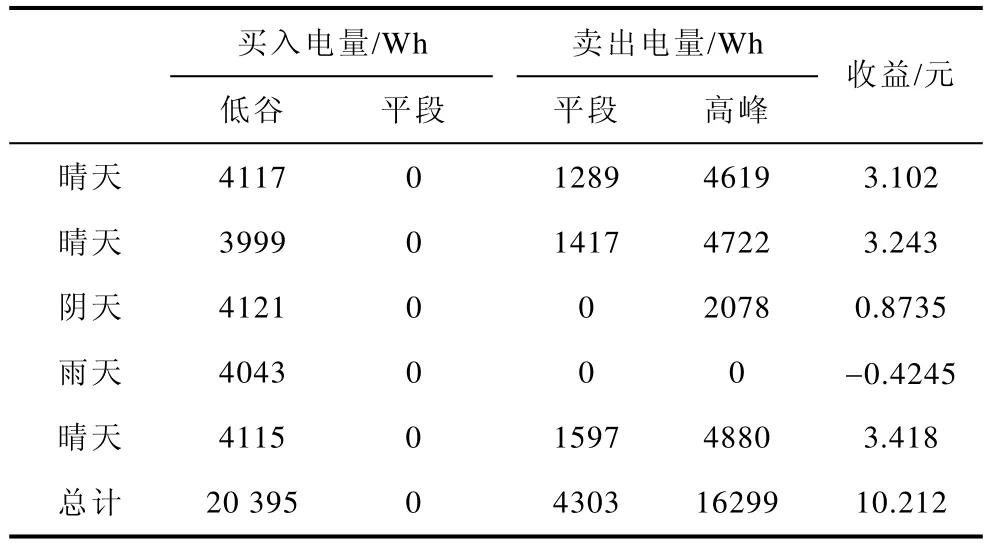
表3 系统运行收益Tab.3 Gain of operation

从表中可以看出，模糊控制策略使得分布式发电系统在电价低谷时买入电能, 在电价平段和高峰时卖出电能。分布式发电能量管理系统综合考虑电网电价和发电单元的运行成本，当电网电价较低时，能量管理系统从电网买入电能满足负荷需求和储能单元充电；当电网电价较高时，能量管理系统尽可能地使用当地发电单元满足分布式发电系统的全部需求，并且不向电网买入电能。对于整个分布式电网而言，这种行为是有利的。因为在需求高峰时，基于开放式电力市场的电价较高，能量管理系统能够部分或者全部地满足其内部需求，将有助于减轻电网的阻塞。对于分布式发电系统而言，能量管理系统考虑了市场价格、负荷需求和发电单元运行成本，系统运行期间不仅获得运行收益10.212元，完成了系统的运行成本最优化，还缓和了高峰期间的电力供需矛盾，补偿了电网调峰成本。

5 结论

分析了分布式发电系统的系统结构和能量管理策略，提出了一种基于模糊控制的分布式发电能量管理控制算法。在维持系统能量供需平衡的基础上，该算法根据蓄电池的剩余容量和预测的光伏阵列发电量将系统运行分为稳定运行和经济运行两种运行模式，保证了储能单元的性能和寿命。采用光伏阵列发电预测模型的预测发电量作为能量管理控制算法的输入参考量，解决了光伏阵列输出电能的随机化问题。建立了基于发电预测和运行成本最优化的分布式发电系统模拟运行模型，模拟运行结果表明，通过对发电单元的输出电能预测和储能单元剩余容量预测，系统可以根据实时运行状态进行模式切换；同时，在电网电价变化时，系统能根据模糊控制规则快速地寻找新的工作点，实时调控发电单元和储能单元，优化了系统运行成本。

本文的模型仅考虑了电力市场实时电价对分布式发电系统能量管理的影响，未计及输电约束和分布式发电系统的能量管理策略行为对电力市场均衡的影响，因此如何进一步优化模型，是下一步要做的工作。

[1] Vovos P N, Kiprakis A E, Wallace A R, et al.Centralized and distributed voltage control: impact on distributed generation penetration[J]. IEEE Transactions on Power Systems, 2007, 22(1):476-483.

[2] Katiraei F, Iravani M R. Power management strategies for a microgrid with multiple distributed generation units[J]. IEEE Transactions on Power Systems, 2006, 21(4): 1821-1831.

[3] Gil H A, Joos G. Customer-owned back-up generators for energy management by distribution utilities[J].IEEE Transactions on Power Systems, 2007, 22(3):1044-1050.

[4] Hiscock N , Hazel T G, Hiscock J. Voltage regulation at sites with distributed generation[J]. IEEE Transactions on Industry Applications, 2008, 44(2): 445-454.

[5] Jewell W T, Unruh T D. Limits on cloud-induced fluctuation in photovoltaic generation[J]. IEEE Transactions on Energy Conversion, 1999, 5(1): 8-14.

[6] Mellit A, Arab A H, Khorissi N, et al. An ANFIS-based forecasting for solar radiation data from sunshine duration and ambient temperature[C]. IEEE Power Engineering Society General Meeting, 2007.

[7] Sera D, Teodorescu R, Hantschel J, et al. Optimized maximum power point tracker for fast-changing environmental conditions[J]. IEEE Transactions on Industrial Electronics, 2008, 55(7): 2629-2637.

[8] Kem E C, Culachenski E M, Ken G A. Cloud effects on distributed photovoltaic generation: slow transients at the gardner, massachusetts photovoltaic experiment[J].IEEE Transactions on Energy Conversion, 1989, 4(2):184-190.

[9] Chakraborty S, Weiss M D, Simoes M G. Distributed intelligent energy management system for a single-phase high-frequency AC microgrid[J]. IEEE Transactions on Industrial Electronics, 2007, 54(1):97-109.

[10] Favuzza S, Graditi G, Ippolito M G T, et al. Optimal electrical distribution systems reinforcement planning using gas micro turbines by dynamic ant colony search algorithm[J]. IEEE Transactions on Power Systems, 2007, 22(2): 580-587.

[11] Tsikalakis A G, Hatziargyriou Nikos D. Centralized control for optimizing microgrids operation[J]. IEEE Transactions on Energy Conversion, 2008, 23(1):241-248.

[12] Yudong T, Hongkun S, Funian H, et al. Investigation on TOU pricing principles[C]. 2005 IEEE/PES Transmission and Distribution Conference &Exhibition: Asia and Pacific Dalian, China, 2005.