基于ANSYS的空气静压轴承有限元分析

李华川，苏 茜

（广西机电职业技术学院，南宁 530007）

板形仪是应用于冷轧生产线上板形控制系统的一个关键部件。空气轴承式板形仪主要由若干个空气静压轴承辊环组成。其通过测量辊环气膜压力来测定带材的张应力分布，以期获得良好的冷轧带材板形质量。研究空气静压轴承辊环气膜压力分布时，传统工程方法往往非常烦琐，而采用有限元法不仅灵活，而且精度也高。

1 有限元模型的建立

1.1 理论假设与简化条件

考虑到空气静压轴承辊环的倾斜，其结构一般采用偶数排供气孔；同时，辊环尽可能窄才能精确测出板带沿宽度方向的张应力分布，所以这里采用等分宽度的双排节流孔（即节流孔到轴承端面的距离为1／4辊环宽度，双排节流孔对称分布）模型来分析。该轴承的结构如图1所示。图1中轴承直径D＝4 mm；节流孔为两排，每排节流孔个数n＝8；长径比L／D＝1；l／L＝1／4；节流孔直径d＝0.3 mm；供气压力ps＝0.4 MPa；p0为出口大气压力，p0＝0.1 MPa；h0为气膜平均厚度。

图1 算例结构图与剖面图

该轴承不仅宽度方向左右对称，而且板形辊环两半圆流场也对称，因此，取1／2宽度和1／8圆周的轴承为研究对象。取1，2，3，4四个节流孔附近的气膜分别分析。首先，将气膜按节流孔数目在圆周方向上4等分。每一等份包含一个节流孔，可近似认为每一块气膜厚度不变，即hi＝hop（1-εcosαi）。式中：i表示节流孔号，i＝1，2，…，8；hop为最佳气膜厚度，取hop＝0.03 mm；ε为偏心率，取ε＝0.3；αi为节流孔的位置角，

由于空气静压轴承的平均气膜厚度非常小，与气膜的长度L、宽度D相差百倍甚至更大，这使ANSYS的使用受到了限制。为此作如下假设，以简化模型［1］：

（1）两个节流孔之间无气体流动；在宽度方向上每等份内两节流孔间压力相等，其值为该等份节流孔压力pd；气体无环向流动，仅沿轴向流向端面，其压力由出孔后的pd降至端面的环境压力pa。

（2）气体为等温层流流动。

因此，在求解压力分布时，只需研究每个等份中从节流孔到轴端一段即可。

1.2 边界条件［2］

1.2.1 速度边界条件

气体的分子运动论中，气体分子被看成随机碰撞的颗粒，两次碰撞之间所飞行的平均路程称为平均自由行程λ。，P为气体真空度（torr），一个大气压的真空度为760 torr。若以平均自由行程和气膜厚度之比表示Knudsen数，即Kn＝λ／h。当Kn＜0.01时可以把气体视为连续介质。本模型进气压力为0.4 MPa，气膜厚度h为0.03 mm，则λ＝1.645×10-5（mm），Kn＝因此，可视轴承气膜内的气体为连续介质。根据连续介质气体动力学可得，轴承内壁表面边界的地方，气体分子和壁面之间相对速度为零。即，在壁面处气体分子的速度和轴承表面的速度相等。这样在静态设计中，壁面的速度边界条件（包括x，y分量）为0。

1.2.2 压力边界条件

气体润滑问题中，和大气相通的边界处有压力相容条件：

式中：pa为出口边界压力。

1.2.3 对称边界条件

对称边界系指压力场沿该边界的两侧是对称的。在对称的边界上，有：

式中：n为边界的法线。轴承的几何对称线是对称边界，压力沿这个对称线方向的梯度为零。

1.2.4 ANSYS模型边界条件加载

根据假设理论可以建立简化的有限元模型以分析气膜压力分布。由于气体一维地沿轴向流向出口，可以把气膜沿轴向分为若干流面（图1）进行有限元分析。以第4孔为例的有限元模型如图2所示（其他孔处类似）。其中，CD边为小孔节流器气体入口，AB，BC，CD，DE，EF边为轴瓦；HG边为轴；FG边为对称边界；AH为气体出口。整体上看BCDE为节流器剖面，AFGH为气膜剖面。在模型上加载的边界条件为：CD边供气压力为0.4 MPa，AH处出口压力为0.1 MPa。其余各边速度的x，y方向分量均为0。图2网格的划分使用了映射网格而不是自由网格，可以使网格划分大致体现出速度矢量的流向，使结果更加精确。

图2 有限元ANSYS模型

2 有限元计算结果

通过在ANSYS软件内设定模型气体特性与环境参数，并将模型速度、压力、对称边界条件进行加载，利用ANSYS的前处理模块和流体动力学分析计算模块可得到每个节点的压力和每个单元的流率分析结果。因篇幅原因，仅列举3号孔和4号孔的有限元分析结果。

（1）图3、图4为节流孔处气膜速度矢量图。由图3、图4可看出气流由节流孔流出，流入平均厚度只有0.03 mm的气膜。由于从大尺寸空间流入小尺寸空间，气流在这一部分的流速增大约百倍；并且由节流孔至左边端面出口，流速逐渐减小，但可看出出口处速度仍然较大。同时，模型右半部分气流流速很小并逐渐至零，符合模型在宽度方向上对称的两节流孔间压力相等，无气体流动的条件假设和实际情况。

图3 3号节流孔处气膜速度矢量图

图4 4号节流孔处气膜速度矢量图

（2）由图5可看出，速度矢量表示的流动方式除由节流孔进入气膜时出现一部分紊流外，其余均与假设理论和流动特性所用的假设（气体为等温层流流动）一致。另外，如果希望节流孔进入气膜部分也较好的符合层流流动，设计时可使节流孔下端有一定弧度。

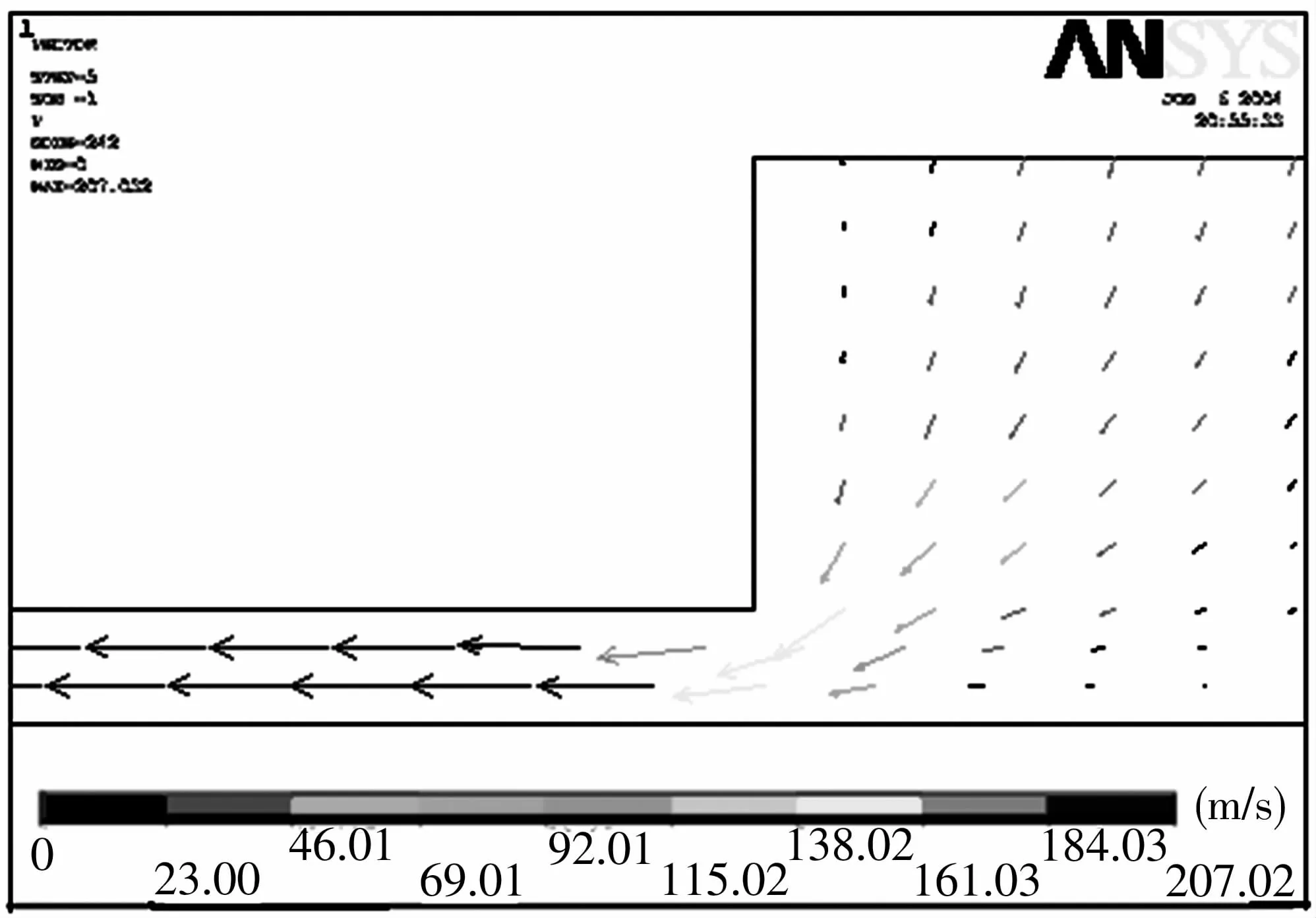
图5 4号节流孔处气膜速度矢量图（局部）

（3）在空气静压轴承辊环的设计过程中，气膜压力场的计算是设计成功与否的关键之处。图6、图7为气膜压力分布图。从图中可看出，节流孔处气膜压力最大，离节流孔越远处压力越小。3号节流孔单元气膜压力大于4号节流孔单元，这与实际情况吻合，气膜压力会随气膜厚度减小而增大。根据节流孔处气膜厚度公式推算，3号节流孔单元气膜厚度小于4号节流孔单元的气膜厚度。实际情况也是如此，轴在外载荷作用下产生向下的偏心，故从1号节流孔至4号节流孔，气膜厚度逐渐增大，气膜压力逐渐减小。

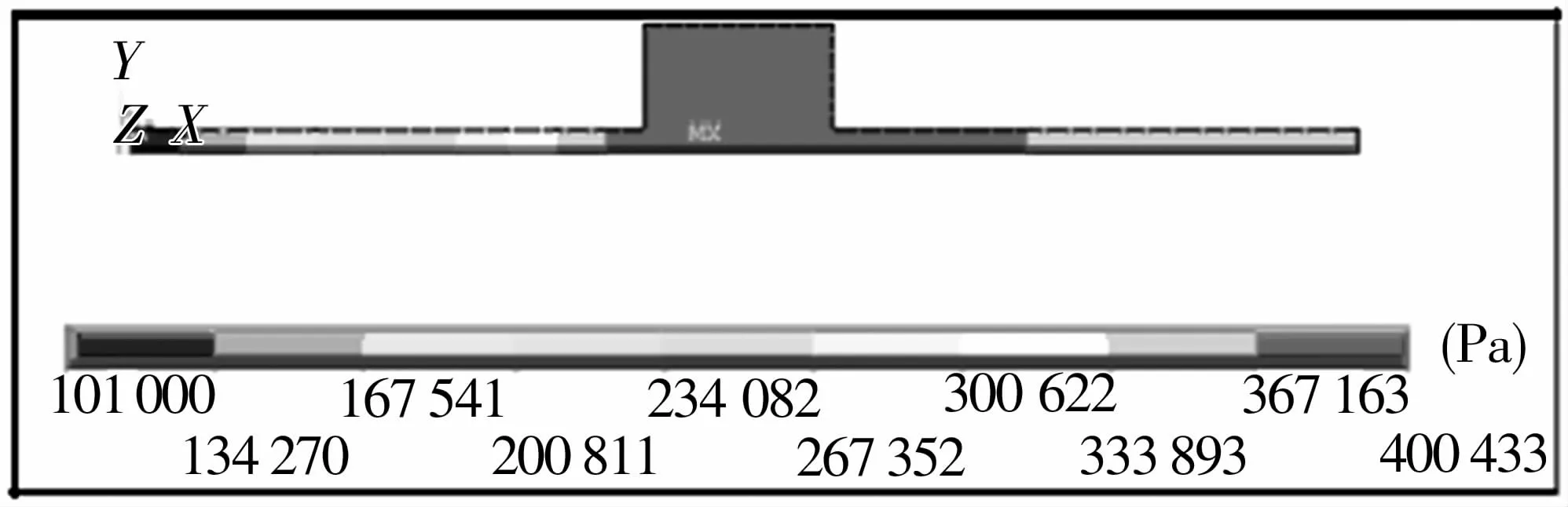
图6 3号节流孔处气膜压力分布图

图7 4号节流孔处气膜压力分布图

（4）图8、图9为轴颈表面压力分布图。从图中可看出3号节流孔单元和4号节流孔单元的轴颈表面压力分布变化趋势相似，但变化量不同。即沿轴颈各处受力存在差异。这可能使轴承发生对自身有害的自激振，虽然很难避免，但应尽量减小振动幅度。由于轴颈表面压力主要来源于气膜压力，故其分布情况与气膜压力分布相似。在每个节流孔单元中，节流孔处轴颈表面受到的压力最大。随着气膜厚度的增加，轴颈表面压力分布呈减小趋势。

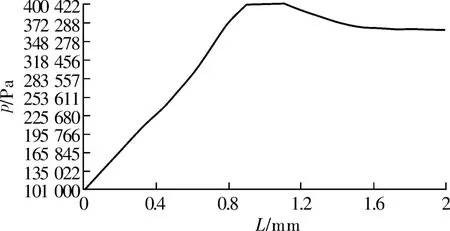
图8 3号节流孔处轴颈表面压力分布

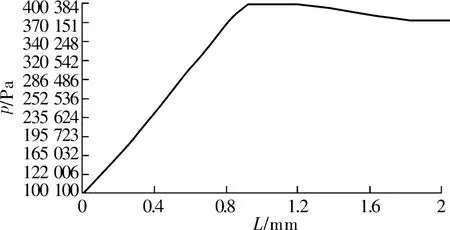
图9 4号节流孔处轴颈表面压力分布

3 轴承承载能力与刚度计算

根据文献［2］提供的气体静压轴承传统工程设计理论，并用VB程序开发计算该模型，可计算出实际值大约为W＝1.681 5 N［3］，可得文中的ANSYS计算结果与文献［3］的传统工程设计方法计算结果相差6.6%，基本一致，由此可知采用ANSYS对空气静压轴承进行有限元分析是可行的。

4 结束语

ANSYS对空气静压轴承进行分析的结果与轴承实际工作情况基本一致，基于其分析结果所得到的轴承承载能力和静刚度与传统工程理论设计方法计算结果接近。由此说明，此有限元分析方法具有较好的精度，采用该方法对空气静压轴承进行研究是可行的，可为空气轴承式板形仪的结构设计和性能特性分析提供理论依据。此外，可以考虑使用三维形式建立模型，这样会使有限单元网格划分更加精确，分析结果更加准确。