由一道月球绕地球公转周期习题解法引起的思考
2010-07-25吕铭
吕 铭
(南京师范大学物理科学与技术学院,江苏南京 210046)
在求解物理问题时,有时会遇到运用等时性的思想方法来解决的问题.我们在处理这些问题时虽然数学表达上是严密的,但是却加大了运算量把题解得不够“物理”.有时我们运用了一些物理中的思维方法,但是却存在逻辑上不够严密的问题.这些对于学生来说是都有一定的弊端,学生的物理概念以及思维方法都是在潜移默化中建构起来的.我们一定要弄清楚整个分析过程以及数学近似的来龙去脉,让学生透彻地学习与掌握知识以及处理问题的科学方法.若不这样就会对物理过程产生误解,并导致产生错误的认识.下面通过一道有关运动学的例题来说明此问题.
例1[1].已知地球上观察月亮从圆月(望月)到下一个圆月的周期为Tm=29.5(天),地球绕太阳公转的周期为Te=365.25(天),问月亮绕地球的公转周期 T为多少?
解法1[1]:假设地球绕太阳的轨道、月亮绕地球的轨道近似为圆轨道,并认为月亮、地球、太阳始终在同一平面内.
首先,从图1中可看到,当地球从D运动到E的整个时间,月亮正从 A运动一个周期后进一步抵达C.假设月亮在 A、C正好都是圆月(这是地球上看到的月亮全部被太阳照亮).显然,月亮经历的时间并不是月亮绕地球的公转周期,而是在公转周期后再加时间 T′.月亮从 A到B经历的时间才是月亮绕地球1周的公转周期.(注意,这里把B、C画在同一个圆上了,实际上,B应在地球未到达E的圆上.)
利用图中所表示的时间写出关系式

为求 T,必须先求 T′.利用地球绕太阳的时间和角度关系得

再利用月亮绕地球的时间和角度关系

联立上述3个方程,可得

质疑1:当月球从B绕到C转过θ角度时,实际上地球在这个时间段里并不是静止的,两者在上述解法中并不满足严格意义上的等时性,而从式(2)与式(3)的对比中却表明两者是转过了相同的角度.从逻辑上来讲,有理由肯定解法1是有问题的,但是从文献[2]中知道(4)式的答案却是正确的.这里可以做这样一种推测,题目在求解中肯定用到了近似,那么解法1是在哪里用到了近似呢?这样做近似的理由是什么,到底哪里是问题的突破口?我们通过以下的解法来作进一步探析.

图2
解法2:参见图2,设开始太阳、地球、月球三者成一直线,O点表示太阳,A点表示月球.大家知道当月球绕地球公转1周(T)在地球右侧(即 B点处),这时太阳、地球、月球三者不在同一条直线上,而要再次看到满月需要月球转动 θ(即 C点处)所用时间为

又从题设条件知道地球绕太阳公转1周需要 Te=365.25(天),则由此可得θ的关系式

一开始假设地球旋转θ角后就不动了,这是不够准确的.那么假设在月球转过θ的这段时间内地球又转过θ1,那么以同样的假设可知地球转过θ1之后停下来,这时月球经

的时间回到满月的位置.依此类推得

由条件易知

所以原式

质疑2:我们已经看出文献[1]在诠释等时性时是有误的.而解法2是从严格的数学分析出发的,虽严密但多了些“数”的味道,少了些“理”的风采.那么能不能撇开大量的数学运算而又抓住物理的实质呢?答案是肯定的.接下来可通过第3种解法来分析这个问题.
解法3:等时法.如图3,假设在月球的左侧非常近的地方有一个卫星D也参与了绕地球转动且转动周期与月球绕地公转周期相同.开始太阳、地球、卫星、月球四者成一直线,O点表示太阳,B点表示地球,D表示卫星,C表示月球.当经过时间 t地球绕太阳转过θ角度后,发现 O、B、D在同一直线上而C转过1周后仍在地球的右侧,则有


图3
即

其实解法3的实质是将一个物体运动分解的多个过程类比成两个物体运动的同一过程,但是这两个物体的运动存在着指定的约束,从而省略了较为繁琐的数学推导过程.至此我们得到了与解法1和解法2相同的答案,也显示了物理过程的实质.解法3解答了从解法2中留下来的的质疑,过程简洁清晰.
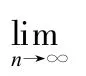
质疑3:等时法的过程明了,步骤清晰.那它还可以在哪些题中体现优越性呢?下面再举两例.
例2[3].速率为30 km/h的两列火车在相挨并行的轨道上相向而行,当两火车相距60 km的时候,一只每小时能飞60 km的鸟离开一车直向另一车飞去,当鸟到达另一车时就立即飞回第一车,以后就继续这样来回的飞.问:鸟一共飞了多少距离?
解法1[3]:我们着眼于一个物体运动分解的多个过程.两车各行驶30 km时相遇,经过的时间为1 h,因而鸟也飞了1 h.当鸟从甲往乙飞时,取甲为参照系,从甲往乙飞的方向为正方向,则乙车 v乙=30 km/h,方向为负,鸟对甲的速度为 v1=30 km/h,方向为正,第1次与乙车相遇,得

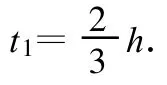

第2次飞行:鸟到达乙后,立即回头向甲飞.这次飞行和第1次不同,因为取甲为参照系,甲是不动的,但鸟和乙同时一直向甲前进,乙的前进不影响第2次飞行,但却使第3次飞行距离变短了.
设第2次飞行需时 t2,鸟飞行的距离为 d2,第2次飞行鸟的速度为 v2=90 km/h,方向为负,则

将t1的关系代入得
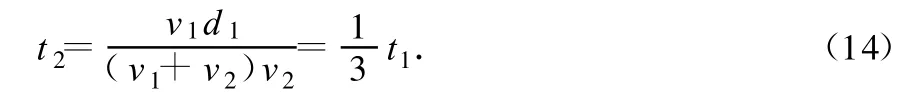
第2次飞行结束时,甲,乙相距


即

所以鸟一共飞行的距离为

解法2:等时法.这里不像例1解法3一样需要构造一个等时性模型.我们很容易知道火车所用的时间与鸟飞行所用的时间相等.设火车所用时间为t,鸟飞行速度为v,两列火车的速度分别 v01,v02,则知

因为鸟的速率保持v,且运动不间断,则鸟所行的路程为

例3[1].A、B、C 三个芭蕾舞演员同时从边长为l的三角形顶点 A、B、C出发,以相同的速率 v运动;运动过程中始终保持A朝着B,B朝着C,C朝着A.试问经多少时间3人相聚?每个演员跑了多少路程?

图4
解法 1[1]:如图 4,仍然着眼于一个物体运动分解的多个过程,并根据小量近似有

所以


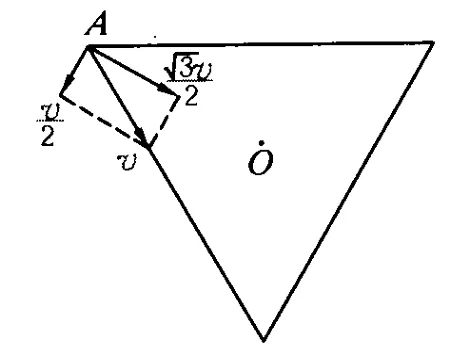
图5


进而可得

综合以上3例可以看出,对于这样一类速率始终不变,物体最终到达的位置是易于判断的物理问题.可以着眼于一个物体运动分解的多个过程的方法来处理,但是其中用到了较为繁琐的小量近似以及极限思想;我们又可以着眼于等时性的原理将运动物体的内在约束找到,往往能将问题简单化.
1 王建忠.启东中学奥赛训练教程◦高中物理(第2版).南京:南京师范大学出版社,2006.68-69
2 高崇伊.地球和月球的公转周期与自转周期.物理通报,2003(7):17-18
3 范小辉.新编高中物理奥赛实用题典.南京:南京师范大学出版社,2008.2-3
