基于LFSR状态相关的测试数据压缩方法*
2010-07-25梁华国程旺燕
毛 蔚 ,梁华国 ,程旺燕
(1.合肥工业大学 计算机与信息学院,安徽 合肥230009;2.合肥工业大学 电子科学与应用物理学院,安徽 合肥230009)
随着电路复杂程度的提高和尺寸的日益缩小,特别是进入深亚微米以及超高集成度的发展,通过集成各种IP核[1]系统级芯片的功能更加强大的同时也带来了一系列的设计和测试问题。例如,如何压缩迅猛增长的测试数据就是设计者、EDA工具厂商面临的挑战之一。
在传统的测试生成方法中,测试生成过程长、测试复杂程度高、故障覆盖率低。一种高效、经济的测试方法是使用内建自测试(BIST)[2-3]来代替传统的方法,它通过在芯片内部集成少量的逻辑电路实现对整个电路的测试。内建自测试(BIST)是近年来研究的热点,而使用线性反馈移位寄存器(LFSR)[4]生成测试模式的伪随机内建自测试,已经被学术界、工业界广泛地使用。
在内建自测试中,一种使用LFSR重新播种的方法得到了普遍应用[5]。LFSR重新播种方法的核心思想是将确定测试向量集编码成LFSR种子,而种子是需要装入LFSR的一组位序列,通过运行LFSR,可将种子扩展为所需要的确定性向量,然后送入扫描链。
1 编码理论及实现策略
1.1 LFSR编码
线性反馈移位寄存器常用来组成测试向量生成器,它由互连的寄存器和线性逻辑单元(异或门或同或门)组成。一个伽罗华域GF(2)上的n级LFSR结构图如图1所示[6],其中hi=1表示反馈线路接通,hi=0表示反馈线路未接通。
图1的特征多项式为f(x)=1+h1x1+h2x2+…+hn-1xn-1+xn,该 LFSR的状态转移矩阵 Φ 为[10]:


图1 n位反馈移位寄存器的结构
在LFSR重播种方法中,求解LFSR种子时,通过选定的特征多项式,建立状态转移矩阵,结合测试向量建立方程组,若方程有解,则编码成功;否则编码失败。
1.2 方案实现策略
在LFSR重新播种方法中,为使LFSR能成功编码测试集中所有的测试向量,其度数受测试集Smax的制约;若能降低Smax的值,就可以降低LFSR的度数,也就能提高数据压缩率和编码效率[4]。在本文方案中,结合了完全测试向量切分方法,根据测试向量的长度,为了使控制简单,把所有向量切分成两个等长的向量,这样可以降低Smax的值,达到减少种子位数的目的。例如,将一个18位的测试向量a0a1…a17=x1x0101x110111xxxx切分成等长的两部分,得到两个连续的测试向量b0b1…b17=x1x0101x1xxxxxxxxx和 c0c1…c17=10111xxxxxxxxxxxx。 其中粗体部分分别为和,剩余部分由无关位填充,切分后生成的测试向量确定位数大大降低,编码成功率将会显著提高。可以求解得b0b1…b17和c0c1…c17的种子,分别为s1=110和s2=101,将种子展开后形成的测试序列分别为v1=110010111001011100和 v2=101110010111001011,只要将v1和v2的黑体部分组合起来,就可以得到测试向量 v=110010111101110010,它与 a0a1…a17是相容的。 在实际操作中,只需在装载s1后,经过9个时钟周期再装载s2,就可以生成测试序列 v。
在传统的LFSR重新播种方法中,分别对每个测试向量进行编码,求解出测试向量的种子,计算出种子后,将种子施加到LFSR上,LFSR则利用种子来生成测试向量。记LFSR的初始状态为S0(即为种子),当LFSR运行m个周期(m为扫描链的长度),种子扩展为所需要的向量后,再把扫描链的内容加载到电路中进行测试。记测试向量充满整个扫描链时的LFSR的下个状态Sm+1为末态。接着测试电路又载入另一个种子,继续生成测试向量。而由于LFSR的末态和种子集S中某一种子存在某种关系,它们可能仅有部分不同位,举例如图2所示。

图2 种子的处理
在图 2中,对应种子 s1的末态是 010011,对比 s2、s3、s4,此末态与种子s3之间的变化位最小,即海明距离最小。此时,当载入完s1后,接着载入s3,在载入下一个种子s3时,可不必载入该种子的全部位,只需改变相应位的寄存器值。定义种子格式在原种子后加入控制位,以确定需要改变哪些寄存器值。当载入完s1后,其末态的第4位需要翻转,记录信息为100。
1.3 选择排序策略
对于种子Si=b0b1…bN-1,bi表示各种子位数,LFSR运行Si后的末态为:
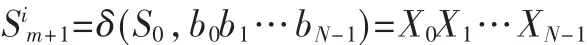
种子集S按上述方法生成对应的末态集合M。为使得在载入下一个种子时需改变的寄存器数量最少,需找到一个种子与此时LFSR末态相同位尽可能多,即海明距离尽可能小。
从全局来讲,目标是要使得所有种子与其上一个末态之间的海明距离之和最小,所以需要对种子集进行排序。从某个种子开始,遍历每个种子,并且每个种子被访问一次且仅一次,其目标是找出一个与末态的海明距离之和最小的种子序列。在这个过程中,会产生带控制位的新的种子序列。该问题为旅行商问题TSP(Traveling Salesman Problem)[7],它是组合优化问题中典型的NP-hard问题,从图论的角度,该问题的数学描述为:
给定无向图 G=<v,e>,其中 V为顶点集(种子集),E为边集,且|V|=n。D=(dij)n×n为顶点距离矩阵,其元素dij表示种子i与种子j末态之间的海明距离,又设π=(π1,π2,…,πn)表示 1,2,…,n 的一个排列,则 TSP 为约束组合优化问题可表示为:

1.4 带多输入端口的LFSR
在本文的方案中使用的是经过改造过的LFSR。对于被测电路的输入,传统的测试方法为每输入一组种子,LFSR就对输入值进行移位、异或运算,并将结果移入扫描链中,接着再输入下一组种子重复上面步骤[8]。由于种子在LFSR中运行的末态数值可能会与其他种子相容或者有很多相同位,如果载入下一种子时仍旧重新载入这些相同位,则会占用大量的存储空间,随着系统的复杂度提高,导致测试向量的增多,测试时间将变长。本方案使用的是多输入移位寄存器,结构如图3所示。
与普通LFSR区别在于,该结构中使用了多路选择器MUX,使得不需要额外的逻辑便可以重载LFSR,在从ROM中载入种子时,所要做的是检测种子集中的相应的控制位,当新种子和LFSR中的寄存器中的内容不同时,重播种电路的输出在相应的多路选择器的选择端置1,载入种子位。该方法可以从各个输入端in并行输入,从而可以提高种子的载入效率,节省测试时间和测试费用。

图3 多输入移位寄存器
2 硬件结构
图4所示为本文方案的解压电路原理框图,该电路主要由一个状态机(FSM)、一个多输入端 LFSR、块计数器、位计数器、模式计数器等器件组成,上一节介绍的编码信息存储在自动测试设备ATE(Automatic Test Equipment)中,在解压时,必须把原测试集中的所有向量还原出来。电路中,块计数器用来进行种子位数的计数,指示LFSR展开得到的当前数据是控制位还是数据位,其初始值是种子的长度,当块计数器计数为0时,控制器输出控制位;位计数器的初始值为目标测试向量的长度;模式计数器用来计算种子数,计数初值是测试向量对应的种子总个数,模式计数器每减1,都会通知ATE向LFSR装载新的种子。
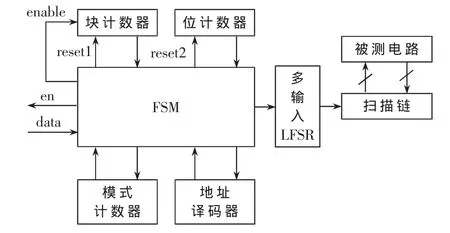
图4 电路结构框图
在测试过程中,模式计数器置为初始值,reset1和reset2信号有效,使块计数器和位计数器复位。ATE按顺序向LFSR装载种子,每载入一个种子都会通知模式计数器进行减1计数,接着位计数器和块计数器同时减1计数,块计数器先减至0,enable信号无效,模式计数器减1;同时控制器将进入测试的种子展开,得到控制位和实际的种子数据;经过若干个周期,位计数器减至0,此时生成一个完整的测试向量,然后根据得到的控制位信息,在当前种子在LFSR中运行周期结束后,地址译码器根据控制信息,选通多输入端LFSR中相应的端口,在相应的LFSR单元中载入下一个种子数据;同时enable信号有效,位计数器和块计数器复位。重复该过程,直到模式计数器减至0,所有的种子施加完毕。
相对于一般的LFSR编码方案,硬件结构中的模式计数器和位计数器是必需的,本文方案只增加了一个块计数器和地址译码器,但由于本文方案大幅度缩小了LFSR的度数,因此相比单独使用LFSR重播种方法硬件开销更小。
3 完整的综合过程
基于多输入端LFSR的测试数据压缩方案的完整综合过程可由下面4个步骤组成:
(1)选择LFSR和期望产生的随机模式数 N,对初始的N个随机模式进行故障模拟,确定出伪随机测试阻尼硬故障集 Fhard,即确定的测试立方集 TD⊂{0,1,-}n;
(2)选择合适的度数,选择不同的特征多项式编码TD,利用上节中介绍的方法使得所有的测试向量均能编码成功,得到种子集S,并记录相应的LFSR;
(3)使用第(2)步中记录的 LFSR,对种子集 S中的每个种子s(i)生成末态m(i),得到末态集合M,利用选择排序策略对S中的种子进行处理排序,最后得到S′;
(4)加载种子进行测试。在测试过程中,处理过的种子集S′经过解压电路,由该LFSR展开成目标测试集。
4 实验结果分析
为了验证本方法的有效性,采用了ISCAS-89标准电路中的 s5378、s9234、s13207、s15850、s38417、s38584 电路,并使用测试生成工具预先计算的测试向量进行实验。本方案实验结果如表1所示,其中,需要说明的是第3栏是种子位数,即LFSR的度数;第4栏是压缩后的总位数TE;第5栏为压缩率,压缩率的计算公式为(TD-TE)/TD,在编码过程中,压缩率会受到种子编码顺序的影响。为了与国际上同类压缩方法进行比较,第6栏列出了混合码[9]的实验结果。由表1看出,本文方案的压缩效果要优于混合码。

表1 本文方案的实验结果及与混合码的比较
本文实现了一种应用LFSR编码的测试压缩数据新方法。在这种方法中,利用了当前LFSR状态和种子的相关性,对载入过程中的种子需要改变的位进行控制,而对种子不需要改变的位保留,从而提高了编码效率和数据压缩率,并在实验中得到了较好的结果。与同类测试数据压缩方法相比,这种方法能很好地提高编码效率。
[1]MOURAD S.Principle of testing electronic system[M].John Wiley&Sons,Inc,2000.
[2]梁华 国,HELLEBRAND S,WUNDERLICH H J.一 种基于折叠计数器重新播种的确定自测试方案[J].计算机研究与发展,2001,38(3):931-937.
[3]HELLEBRAND S,RAJSKI J,TARNICK S,et al.Built-in test for circuits with scan based on reseeding of multiplepolynomial linear feedback shift registers[J].IEEE Trans on Comp,1995,44(2):223-233.
[4]KOENEMANN B.LFSR-coded test patterns for scan designs[C].Proceedings of the european test conference.Munich,germany,1991:237-242.
[5]梁华国,蒋翠云.使用双重种子压缩的混合模式自测试[J].计算机研究与发展,2004,41(1):214-220.
[6]ABRAMOVICI M,BREUER M,FRIEDMAN A.Digital systems testing and testable design[M].New York:Computer Science Press,1990.
[7]GREGORY G,ABRAHAM P.The traveling salesman problem and its variations[M].Dordrecht Hardbound:Kluwer Academic Publishers,2002.
[8]KOENEMANN B,BARNHART C,KELLER B,et al.A smart BIST variant with guaranteed encoding[C].Proceedings of VLSI test symposium,Marina Del Rey,CA,2001:325-330.
[9]WURTENBERGER A,TAUTERMANN C S,HELLEBRAND S.A hybrid coding strategy for optimized test data compression[C].Proceedings of IEEE International test conference,Charlotte,NC,2003:451-459.
