融入中国剩余定理及Montgomery算法的快速RSA算法研究

于丽丽，王丽君

(辽宁科技大学 软件学院，辽宁 鞍山114051)

RSA算法是一种公开密钥算法，其加密密钥和算法本身都可以公开，解密密钥则归用户私人拥有。从诞生那天起，RSA就因为安全强度高、使用方便等卓越性能而受到关注，并得到广泛应用。但是，近年来由于分解大整数的能力日益增强，为保证RSA密码体制的安全性总是要增加模长，使加密、解密操作需要计算的位数达十进制百位以上的模幂乘函数，使运行时间很长，这一直是制约其应用的瓶颈问题，因此本文在速度方面对RSA算法做了相关改进。

本文主要针对RSA公钥密码体制中中国剩余定理的使用以及大整数模指数算法进行了深入的研究。经证明，在RSA算法中使用中国剩余定理可以提高其加密的速度达到之前的4倍。模指数运算是大部分密码算法实现中最耗时的运算步骤，因此模指数运算正是这些密码体制实现的关键，而大整数模运算又是其核心运算。本文将对密码学中的大整数模运算进行研究。

1 利用中国剩余定理提高RSA算法效率

中国剩余定理(CRT)又称为孙子定理，是数论中最有用的定理之一，并在我国科学技术史上对数学的发展作出了重要贡献。

中国剩余定理可有几种不同的表示形式，这里给出其中最有用的一种表示形式，即：

其中 mi是两两互素的， 即对 1≤i，j≤k，i≠j有 gcd(mi，mj)=1。可将ZM中的任一整数对应一个k元组，该k元组的元素均在Zmi中，这种对应关系可表示为：

其中 A∈ZM，对 1≤i≤k，ai∈Zmi，且 ai=Amodmi。中国剩余定理的用途之一是给出了一种方法，使非常大的数对M的模运算转化到更小的数上运算，当M为150位或150位以上时，这种方法非常有效。

1.1 加速算法

在 RSA加密算法中，n=pq(p，q为大素数），因此，在试图计算c≡md(modn)前，可以先计算：

而这两步运算，又因为模数的变小，可以简化为：

然后，根据中国剩余定理，计算出c为：

在这个算法中，假设 n的二进制长度为 k，那么 p，q的 长 度 约 为 k/2。 假 设 d1，d2，p-1(modq)，q-1(modp)都 已知，则整个计算过程约需要3k3/8次位运算。而不用中国剩余定理，则约需要3k3/2次位运算。其中的假设条件，由于RSA系统一经建立，所涉及参数就相对稳定，因而是可以实现的。所以新算法可以切实地将RSA系统的运算速度提高约4倍。加之计算cp、cq的过程相对独立，满足并行计算的条件，因此基于中国剩余定理的改进算法在速度上有着明显的优势。

1.2 出错攻击

用中国剩余定理加速计算RSA体制时，如果由于某些意外满足以下3个条件：

(1)签名(加密)信息己知；

(2)在签名(加密)时出现了一个错误；

(3)错误的签名(密文)被输出。

那么，这个错误就可能导致参数n被分解。

假设，设备在计算 cp时发生了错误，即获得了 cp′，cp′≠cp，而 cp计算正确。 则通过 cp′和 cp，可以计算出一个错误的c′。由此可以得到：

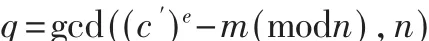
证明：

根据中国剩余定理有

等式成立。

从应用角度来看，出错攻击是一个非常强大的攻击方法。它提醒在设计系统的过程中，必须小心谨慎。因为，只要发生了一个错误，那么整个系统将会面临崩溃的危险。而事实上硬件电子设备出错是时常出现的，所以这种威胁极其现实和紧迫。

对于签名或者认证服务商，还存在一种被称为“否定服务”的攻击。一个攻击者只需要匿名的声称，就能获得服务商的一个错误签名，进而将迫使服务商放弃目前的密钥对。

而对于真正的攻击者，有许多已知的方法可以帮助攻击者实现诱导系统出错，包括重写ROM、修改EEPROM、破坏逻辑门电路等。

1.3 改进方法

几种比较实用的，对抗出错攻击的方法有：

(1)冗余计算 cp，cq的值。对 cp，cq的值各做 2次计算，如果2次结果不同，则废止此次运算；如果结果相同，则计算c值并输出。

(2)增加对c的验证环节。在计算获得密文(签名)c之后，验证m=ce(modn)是否成立。若不成立，则废止；若成立，则输出结果c。

(3)Shamir在1997年提出了一种验证模幂运算的方法[1]。具体到这个问题中，需要随机选取r，并计算：

如果 cpr≡cqr(modr)，则认为计算过程正确，进而计算：

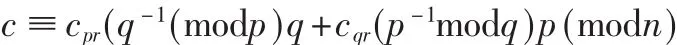
否则，废止此次运算。

事实上，目前己经有很多将此加速算法应用到密码产品中的想法，参考文献[2]就是一个例子。只是它使用了混合半径转换，进一步降低了运算强度，即将

替换为

这是因为：

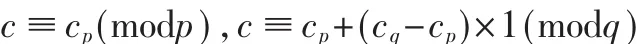
但是，混合半径r的使用，本身并不能回避出错攻击。当cp被错误地计算成cp′时，依旧无法进行有效的验证与更正。因此，这一计算同样会受到出错攻击，需要对其步骤加以调整，增加输出前的验证。由于是硬件实现的问题，因此更适合采用方法(3)。方法(1)意味着运算量加倍，而方法(2)则会需要全程储存被加密信息，方法(3)随机参数的获得可以增加运算过程的随机性，同时验证步骤只是简单的位比对，更加适合硬件实现。

2 Montgomery模乘算法

在没有出现Montgomery模约减算法之前，研究人员用除法求余数的方法进行模约减、模乘等算法，即经典的模约减算法。Montgomery模约减无需使用经典模约减算法而能有效地实现模乘法的技术。

设m是正整数，R和 T是整数，满足 R＞m，gcd(m，R)=1，0≤T≤mR。Montgomery[3]于 1985年提出一种可以不使用经典乘法计算TR-1modm的方法。TR-1modm称为T模m关于R的Montgomery约减。选择适当的R，Montgomery约减可以有效地计算。

如果将m表示成n位的b进制数，那么R的典型选择是 bn。条件 R＞m显然满足，但条件 gcd(b，m)=1当且仅当gcd(b，m)=1时才能满足。因此这种R的选择并非对所有的模数都是可行的。对于RSA算法来说，m是奇数，因此 b可以取 2的幂，且 R=bn。

引理 1 m和 R是整数，满足 gcd(m，R)=1。 令 m′=-m-1modR，T是满足 0≤T≤mR的正整数。若 U=Tm′modR，则(T+Um)/R 是整数，且(T+Um)/R≡TR-1(modm)。

证明：T+Um=T(modm)，因此(T+Um)/R-1≡TR-1(modm)。为了说明(T+Um)R-1是整数，观察到对于某些整数k和1，有 U=Tm′+kR 和 mm′=-1+lR，于是(T+Um)/R=(T+(Tm′+kR)m)/R=(T+T(-1+lR)+kRm)/R=lT+km。 证毕。

(T+Um)R是对TR-1modm的估计。因为T＜mR且U＜R，所以(T+Um)/R＜(mR+mR)/R=2m。因此有(T+Um)/R=TR-1modm或(T+Um)/R=(TR-1modm)+m。即TR-1modm或者等于(T+Um)/R，或者等于(T+Um)/R-m。

如果所有的整数都表示成b进制，并且R=bn，那么TR-1modm可以采用算法1，用两个多精度乘法(U=Tm′和Um)、一次多精度加法(T+Um)和一次右移(即除以 R)计算出来。

算法1 Montgomery模约减算法

输入：整数 m=(mn-1…m1m0)b，gcd(m，b)=1，R=bn，m′=-m-1modR，T=(t2n-1…t1t0)b＜mR；

输出：TR-1modm。

算法步骤为：

(1)A←T；

(2)U←Tm′modR；

(3)A←T+Um；

(4)A←A/bn；

(5)如果 A≥m，则 A←A-m；

(6)返回(A)。

显然，在两次多精度乘法中，算法1需要进行2n2次单精度乘法。1990年，Dusse等人[4]改进了算法 1，他们将步骤(2)和(3)巧妙地融合到一起，新的算法只需要n(n+1)即 n2+n次乘法，见算法 2。

算法2 改进的Montgomery模约减算法

输入：整数 m=(mn-1…m1m0)b，gcd(m，b)=1，R=bn，m′=-m-1modb，T=(t2n-1…t1t0)b＜mR；

输出：TR-1modm。

算法步骤为：

(1)A←T；

(2)对于 i从 0到 n-1，执行：

①ui←aim′modb；

②A←A+uimbi。

(3)A←A/bn；

(4)如果 A≥m，则 A←A-m；

(5)返回(A)。

算法2没有像算法1那样要求m′=-m-1modR，而是要求 m′=-m-1modb。步骤(1)中，当 i=l时，A具有性质 aj=0，0≤j≤l-1。步骤(2)并没有修改这些0的值，但是将 al替换成了0。于是在步骤(3)中，A能被bn整除。

算法2的步骤(1)和(2)总共需要 n+1次单精度乘法，由于步骤(2)需要执行n次，因此单精度乘法的总数是 n(n+1)。此外，还需要少量可以忽略不计的加法和移位等运算，而不需要任何单精度除法。

2.1 SOS模乘法算法

Separated Operand Scanning算法简称SOS算法，是模乘法运算中最基本的方法。即先用传统多精度乘法或其他方法进行多精度乘法运算，然后用算法2进行模约减运算。算法3给出了SOS算法的描述。

算法3SOS模乘算法

输入：整数 m=(mn-1…m1m0)b，x=(xn-1…x1x0)b，y=(yn-1…y1y0)b，gcd(m，b)=1，R=bn，m′=-m-1modb；

输出：xyR-1modm。

算法步骤为：

(1)A←xy；

(2)对于 i从 0到 n-1，执行：

①ui←aim′modb；

②A←A+uimbi。

(3)A←A/bn；

(4)如果 A≥m，则 A←A-m；

(5)返 回(A)。

通过算法3可以看出，SOS算法仅仅是将乘法和模约减算法前后罗列，组合到一起，并没有做实质性改进。该算法效率相对不高，其单精度乘法的次数为2n2+n。但是，由于步骤(1)相对于其他步骤是独立的，因此，在某些特定的环境下，可以采用Karatsuba算法、Comba算法等快速乘法来提高算法3的效率。

2.2 CIOS模乘法算法

Coarsely Integrated Operand Scanning算法简称CIOS算法，是SOS算法的一个改进。Koc等人给出了CIOS的算法描述，并认为CIOS算法是最理想的模乘法算法。该方法将乘法和模约减算法完美地融合为一体，在读写内存等方面节省了许多的资源。算法4给出了CIOS算法的描述。

算法4 CIOS模乘法算法

输 入 ： 整 数 m=(mn-1…m1m0)b，x=(xn-1…x1x0)b，y=(yn-1…y1y0)b，gcd(m，b)=1，R=bn，m′=-m-1modb；

输出：xyR-1modm。

算法步骤为：

(1)A←0；

(2)对于 i从 0到 n-1，执行：

①A←A+xiy；

②ui←a0m′modb；

③A←(A+uim)b。

(3)如果 A≥m，则 A←A-m；

(4)返回(A)。

算法 4实质是将 x×y和U×m两个多精度乘法按照传统乘法的方法结合到了一起。在步骤(2)开始的时候，U是未知的，需要在进行每个 ui×m之前用 xi×y0的值计算出 ui。最终，步骤(2)交替完成了将所有的 xi×y 和 ui×m累加到A的过程。

CIOS模乘法中，单精度乘法的次数和SOS算法一样，也是2n2+n。但是与SOS算法相比，它将两个乘法结合到了一起，减少了一次循环。步骤(3)在实现的时候，可以不进行除以b的移位运算，而是将结果直接保存到A的高一位中。CIOS详细的效率分析，将在下一节中与FIPS方法一起给出。

2.3 FIPS模乘法算法

Finely Integrated Operand Scanning算法简称FIPS算法，在1993年由Kaliski提出，该方法设计思想来源于Comba算法，它采用类似Comba算法的从右向左的按列累加的方法设计而成，将乘法和模约减算法完美地融合为一体。Koc[5]认为FIPS算法的“乘积累加”结构非常适用于数字信号处理器(DSP)等微处理器，是RSA硬件实现中常用的算法，在某些特定的硬件设备上具有很高的执行效率。算法5给出了FIPS算法的描述。

算法5 FIPS模乘法算法

输 入 ： 整 数 m=(mn-1…m1m0)b，x=(xn-1…x1x0)b，y=(yn-1…y1y0)b，gcd(m，b)=1，R=bn，m′=-m-1modb；

输出：U=xyR-1modm。

算法步骤为：

(1)(v2v1v0)b=0；

(2)对于 i从 0到 n-1，执行：

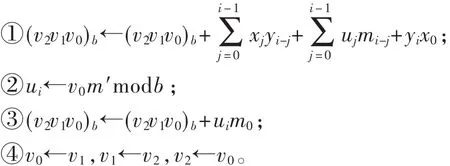
(3)对于 i从 0到 n-1，执行：

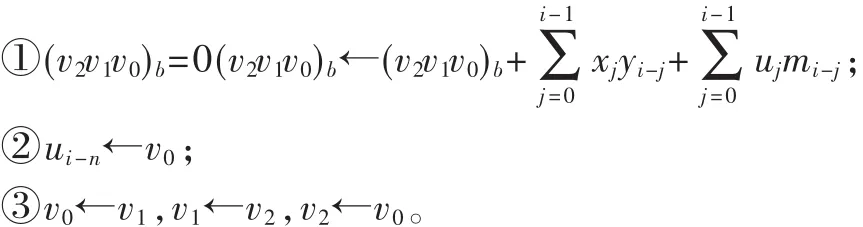
(4)un←v0；

(5)如果 U≥m，则 U←U-m；

(6)返回(U)。

算法 5实质上是将 x×y和 U×m这两个多精度乘法按照Comba算法的方法结合到了一起。在步骤(2)中，分别计算了右边n列的乘积之和，并求出所有的ui。步骤(3)计算出左边的n-2列的乘积之和，同时得到了A=xyR-1modm的值。由于每得到一个ai时，相应的ui值不会被再用到，因此可以直接用 ui来保存ai的值，在编程序时可节省一个长为n的数组。

FIPS模乘法中，单精度乘法的次数和CIOS算法一样，也是2n2+n。但在具体实现时的效率却大大不同。可以根据算法，从理论上统计这两种算法在乘法、加法、读内存、写内存方面的差异。通过表1可以看出，FIPS算法的读内存、写内存次数都远远高于CIOS算法。这是因为由于寄存器个数有限，在计算机程序中，FIPS算法中的三元组(v2v1v0)需要用内存变量来存储，使访问内存所消耗的时间大大增加。但是如果在数字信号处理器(DSP)等微处理器上实现，将会使这些访问内存所消耗的时间忽略不计。因此，在这类硬件上实现FIPS算法，效率将大大提高。如果不考虑三元组(v2v1v0)访问内存的次数，表1将修改为表2。表2中给出的数据可以明显看出，在DSP等硬件上实现模乘法时，FIPS算法仅仅在加法次数上略多于CIOS算法，而读写内存的次数都大大减少，有着很大的优势，非常适合于RSA算法的硬件实现。

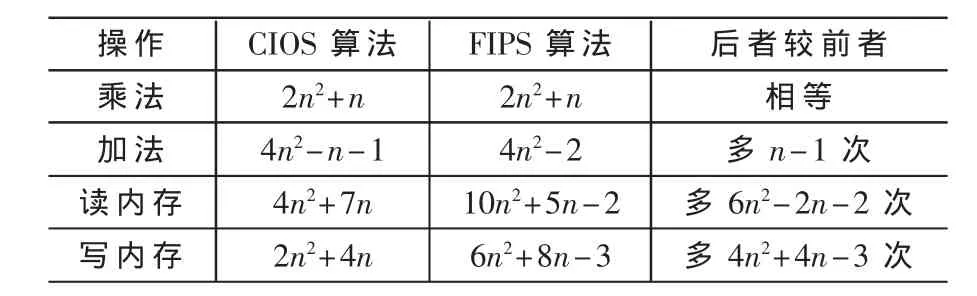
表1 CIOS算法与FIPS算法运算次数统计表

表2 特定硬件上CIOS算法与FIPS算法运算次数统计表

算法速度测试：

测试平台环境为CPU：Genuine Intel(R)CPU 2140@1.60 GHz 1.60 GHz；内存：1 G；操作系统：Windows XP。

综合运用以上3个加速方案，对于一次模幂运算Memodn所消耗的时间 (取50次的平均值)，对比结果如表3所示。

对于RSA密码体制来说，安全性固然是其特征之一，但是加解密的速度却是衡量其算法好坏的首要标准。经过以上分析表明，中国剩余定理可以使非常大的数对M的模运算转化到更小的数上来运算，并且新算法可以切实地将RSA系统的运算速度提高了约4倍。Montgomery模乘算法不仅能够简化RSA算法中的模乘步骤，而且能够有效地节省算法复杂度。

[1]SHAMIR A.How to check modular exponentiation[C].The rump session of EUROCRYPT，1977.

[2]涂航，刘玉珍，张焕国，等.智能卡操作系统中RSA算法的实现与应用[C].第六届中国密码学学术会议论文集，2000：239-243.

[3]MONTGOMERY P.Modular multiplication without trial division.Mathematics of Computation，1985，(44)：519-521.

[4]DUSSE B，KALISHI J.A cryptographic library for the Motorola DSP56000[C].Advances in Cryptology-EUROCRYPT90，1990.

[5]KOC C K.High-speed RSA implementation[C].RSA Labs Technical Report TR-201，1994.