基于FPGA的多项式基下二进制域ECC点乘设计

桂金瑶，陈大军

0 引言

椭圆曲线的实现有软件和硬件两种方式，硬件方式更有安全性。最早硬件实现ECC的设计在GF(2155)上实现了ECC加密算法，加密速度大约为 4× 104bit/s。最早基于 FPGA 实现的 ECC处理器，面积约 5万门，加密时数据吞吐率为1.6× 104bit/s。北京天一集团研制的“天芯一号”高速ECC/RSA密码算法芯片，基于国内可以大规模生产的0.25um工艺进行设计。

目前国内外对于硬件实现ECC的学术成果，主要体现在平衡算法效率和算法所耗费的资源这个过共同的思想。对于ECC加密算法的改进，主要目的就是使改进后的算法更加适用于软件或者硬件实现，一般情况下，二进制域上的椭圆曲线加密算法适合硬件实现，素数域上的加密算法适合软件实现[1]。但是随着加密算法的改进，国内外也出现了很多在素数域上实现椭圆曲线的加密算法[2]。除了区分不同有限域以外，对于硬件电路的实现方式上还有 VLSI实现和FPGA实现两种。这两种实现方式各有优缺点[3]。

为了高效的完成KP的运算，目前国内外有很多不同的算法，如 ADD-DOU算法，加减算法，蒙哥马利算法等。本文采用通过改进的蒙哥马利点乘算法，通过一系列的状态机调用底层模块，并且将模逆模块进行投影映射转换为最少的模乘模块调用设计。根据NIST推荐的5个二进制有限域163，233，283，409，571。本设计的ECC加密算法，基于GF(2233) 域上，通过FPGA设计验证，在50.3MHZ的频率下，逻辑单元个数为25044个，时间和面积复杂度都有一定程度的优势。

1 算法设计

1.1 模乘算法设计

有限域的运算设计以及实现，椭圆曲线密码系统在二元有限域上的运算，尤其是模乘运算极为耗费时间和占用资源。二元有限域上基的选取对模乘运算效率有很大影响，目前普遍使用的是多项式基和正规基。虽然都可以表示乘二进制串的形式，但其对应的有限域运算却是不一样的，正规基表示下的元素运算虽然有利于硬件实现，但是当m较大时，这种基于查表的运算方式，就很耗时并且占用大量的硬件资源。因此，硬件实现二进制域椭圆曲线标量乘法算法时，采用多项式基表示基域是比较理想的。椭圆曲线在有限域内的运算主要有模加，模减，模平方，模乘，模逆。逆元素可以通过有限域上的模平方和模乘来实现（可配置ECC算术模块的设计与实现）追求高效的模乘算法中，Montgomery模乘算法无疑是非常有效的。基本算法是 1985年 Peter L.Montgomery于1985年提出来的，原有复杂耗时的除法运算被一系列的简单移位运算所代替，可以极大的提高模乘运算的效率。从最近的国内外最新出现的模乘算法都是从Montgomery算法的基础上改进得到的。

在本文中，主要是对于二进制域的运算进行研究，GF(2m)是GF(2)的一个扩展，这里的m是扩展的有限域的度。GF(2m)可以被下面的式子来表达，，1≤k≤m。这个多项式是不可约的a可以表示为

其中的系数ai是二进制域里面的元素。这个系数可以是0或者1。通过这 样有效的计算，多项式就可以被储存和表达为比特流的形式。两个二进制域的元素 , (2m)a b∈GF可以被定义为两个多项式系数的相加，公式1

二进制的加法元素ai＋bi对应的就是逻辑的异或操作，对于软件和硬件都可以很有效简单的实现。同样对于模减操作只需要进行一个反转就可以了。

二进制域模乘运算可以分解成两个步骤，首先假设两个操作数a,b∈GF(2m)，模乘的多项式展开为公式2

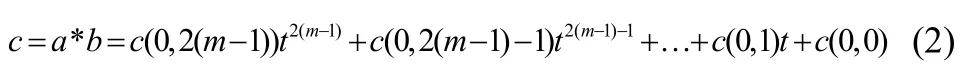
其中，第二步要引入一个最简多项式M，这 个多项式的度必须在小于 m，c0=cmodM，deg(c0)＜m, u,v是二进制域内任意的多项式满足条件u≡u＋vMmodM，为了提高模乘的效率，公式可以变形为tm≡M-TmmodM,因为c的度小于 2m-1，c可以被拆分为两个多项式c1和c2， deg(c1) ＜m- 1， deg(c2)＜m。c=a*b=c1*tm＋c2此时公式3

因为deg(c1) ＜m- 1，deg(M-tm)＜m， 可 以 得 出deg(c1) ＜ 2m- 2，依次迭代，cj可以被分解为多项式cj,x和cj,y，cj＋1=cj,x*(M-tm)＋cj,y， 直 到cj,x=0 ＜=＞ deg(cj)＜m。迭代出来最小的值取决于取最简多项式M的度取到最大值的时候。公式4

2 设计方法与验证

2.1 模乘模块设计

移位操作在软件实现中极其费时，但是在硬件实现中因为对位的操作很简单，所有相对容易实现，对于硬件实现的结构，又可分为多项式比特流全串行结构、全并行结构以及串并混合型结构。在全并行结构中，全部的计算过程都必须在一个时钟周期内运行，这对于器件的要求非常严格，因此在硬件环境受限制的条件下是不合适的。串型结构和并行结构相比，前者面积复杂度更低，但是运算速度偏慢。混合型结构通常用于均衡速度和面积的复杂度。如 LSD（最低数字优先）乘法器和MSD（最高数字优先）乘法器。

基域GF(2m)中多项式基表示下元素乘法一般采用先相乘后模约的方法。元素相乘采用从高到低为扫描和低到高位移位相结合的方法，比较一个2m比特的二进制串。在二元域进行取模运算，实际上就是比较被求模数的最高位是否为高电平，是则被求模的数与模进行异或，否则不变，因此，可以将第一位作为控制位，用以做一个二选一电路。一个输入为为模f(x)，另一个输入位为低电平，当最高位为高电平时，二选一电路输出为模f(x)，反之为低电平。

2.2 模逆模块设计

模逆操作开销比乘法运算的开销大得多，为了有效的减少有限域求逆的操作次数，在进行椭圆曲线点运算的时候需要进行坐标系的转换。点运算之前，要先调用仿真坐标到射影坐标的转换模块，将仿真坐标系下的点转换到射影坐标系下的三维坐标。这样在点运算时只对X、Z坐标进行操作，这两个坐标的转换只需要设计仿真坐标中的横坐标的转换，因此，模块输入坐标是两维坐标中的一个坐标，输出的坐标是三维坐标中的两个坐标，这只需要寄存器之间的简单赋值操作即可。

执行完标量乘法之后，还需要调用射影坐标到仿真坐标的转换模块，将射影坐标的坐标转换乘仿真坐标系的形式，模块接收到标量乘法运算结束的标志以后，将Ready信号置为高电平，之后进行坐标的转换。

在模逆运算时需要使能模平方与模乘操作，所以要用一个使能信号与模乘、模平方之间需要一个多路选择器进行仲裁，以免发生多驱动问题。

2.3 点乘设计与实现

ECC密码体制内运算是有层次性，本设计采用前文中改进的蒙哥马利算法。在硬件的总体架构设计中，对于底层的二进制域的计算，采用了基础运算模块实现运算，而对于上层的如点加、点倍等操作，以及最后的关键的点乘操作，都是通过一系列的状态机调用其下一层的操作来实现的相关功能，计算的中间结果也需要暂存，所以除了控制逻辑与运算组合逻辑之外，还要设计数据存储单元，用一组三端口的寄存器堆实现。

Kp运算模块的结构见图一，在它的组成部分中，有限域运算模块包括乘法运算器，求逆运算器，加法及平方运算器，负责完成有限域上的各种算术运算功能。移位寄存器为线性反馈寄存器，其中保存运算的元素值。点加和点倍运算为两个独立的单元，分别通过状态机对有限域运算模块进行调度，完成点加和倍点运算，点乘状态控制器根据移位寄存器中存储的数值，选择进行点加或是点倍运算点乘状态机在点乘状态机外部还有一个计数器，移位寄存器每移动两位，计数器则计数一次，当计数器输出值 Q达到一定数值时，运算结束。

图1 KP模块结构图

点乘KP模块的实体描述为：

图2 点乘测试模块

综合上述原理方法，通过采用VHDL语言作为设计工具，对基域为GF(2233)的椭圆曲线进行了设计实现，对结果进行了仿真和综合，所选器件环境为 Cyclone系列的EP2C35F484C5,利用 Quartus Ⅱ平台分析得出时钟频率为50.3MHZ，逻辑单元个数为25044个。表1比较了本设计和一些设计在面积上的数据，所有设计都是采用FPGA硬件设计方案。

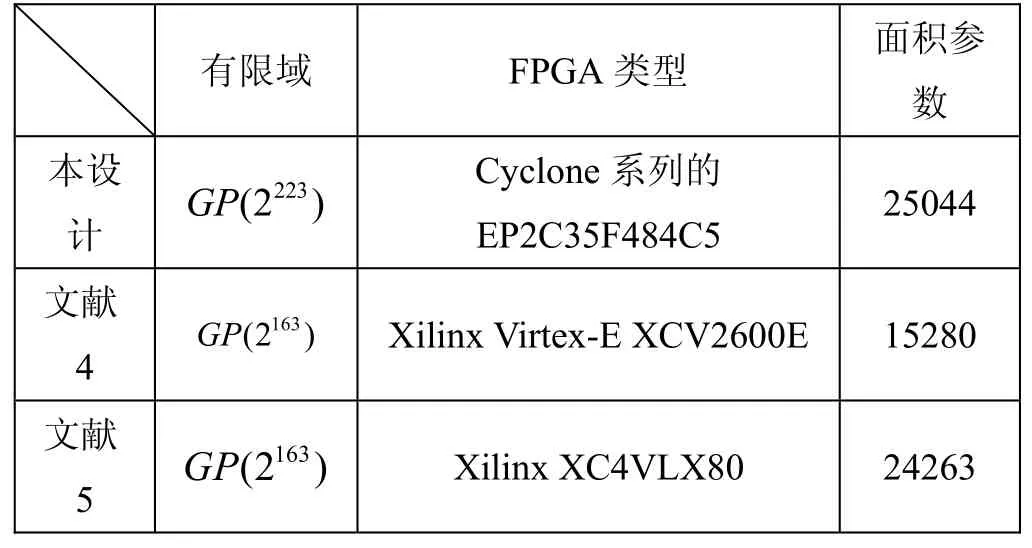
表1 FPGA设计面积比较

3 结论

在椭圆曲线密码体制中，有限域上的乘法运算的效率关系到整个系统的效率，所有重点对其进行了算法上的优化，并且把模逆算法转换乘投影坐标系下，通过更少次的模乘算法进行了实现。本文依据蒙哥马利算法，对其进行了改进，更适合硬件实现，并且消耗的资源更少。通过一系列的状态机调用底层模块，最终基于FPGA实现了点乘算法，速度和面积消耗和经典的实现相比都有相应的优化。

[1]Min C H, Pyo H C, Hoon K C. High Performance Ellliptic Curve Cryptographic Processor Over GF(2163)[C]//DELTA 2008.4th IEEE International Symposium, 2008:290-295.

[2]Mcivor C, Mcloone M , Mccanny J.Hardware Elliptic Curve Cryptographic Processor Over GF(P)[J].Circuits and Systems:RegularPapers, IEEE Transactions,2006,53(9):1946 -1957.

[3]Gang Chen,Guoqiang Bai, Hongyi Chen.A High-PerfomanceElliptic Curve Cryptographic Processor General Curves Over GF(P) Based on a Systolic Arithmetic Unit[J]. IEEE Transaction on Circuits and Systems, 2007,54(5): 412-416.

[4]William N,Chelton,Mohammed Benaissa. Fast Elliptic Curve Cryptography Cryptography on FPGA[J]. IEEE Transaction on Very Large Scale Integration Systems,2008,16(2): 198-205.

[5]H yun Min Chio,Chun Pyo Hong,Chang Hoon Kim. High Performance Elliptic Curve Cryptographic Process Over GF(2163)[C]//4th IEEE International Symposium on Electronic Design,Application &Test , 2008 :290-295.