应急物流服务网点选址模型研究

骆正清， 苑 魁 （合肥工业大学 管理学院，安徽 合肥 230009）

0 引 言

应急物流是指为控制突发事态的进一步发展，采取非常规方式，向事件影响范围内供应紧急救援物资的最具动态特征的特种物流活动。根据需求，应急物流包括物品获得、运输、储存、包装、配送、分发、回收以及信息处理等功能要素。应急物流管理最重要的一项职能就是向事故地以及潜在突发事故区域提供充足、及时的应急物资。而应急物流服务网点则是以行政区域或地理位置划分临时建立的节点设施，它主要职责是收集本区域范围内的物资供应主体所提供的应急物资，同时承担部分配送中心的职能，根据需求评估和收集到的应急需求信息，对汇集来的应急物资执行分拣、包装、分发等操作。应急物流服务网点选址决策对于有效实施应急物流至关重要，这是因为将应急物流服务点置于合理的位置，不仅可以降低成本，而且还能够保证提供应急物资的时效性，从而避免可能导致的更大损失。而从整个应急过程来看，应急服务网点的合理布局对应急资源的配置和应急资源的调度也可以起到事半功倍的作用。

选址问题本身是一个非常经典的问题，有成熟的模型进行解决，然而应急服务网点选址问题与传统选址问题具有不同的优化约束与目标，前者时效性可能非常重要，而后者则更加关注的只是成本。鉴于此，在进行应急物流系统决策时，要充分考虑各个应急服务网点的合理布局，并以较低的建设成本、较低的运行费用和较高的系统工作效率等为规划目标。所以在给定限制条件下的选址问题的基础上进行模型改进对应急物流的高效运行具有更现实的意义。

1 给定限制条件的应急服务网点选址模型简介

1.1 问题提出

在一般的应急服务网点选址模型中，通常考虑的是如何选择应急服务网点地址以使任何应急地点一旦发生突发事件，应急服务网点能在最短时间内到达应急地点实施应急救援，或在满足时间紧迫性的前提下，系统运行费用最小。而给定限制条件下应急服务网点选址模型则考虑的是另一类问题：即对于任何应急地点一旦发生事故时，在不考虑应急需求的情况下，确定应急服务网点的地址，使距离应急地最近的应急服务网点到达应急事故地点的时间小于或等于一个规定的值，且需要建立的应急服务网点数目最小。

1.2 基本假设与限制条件

（1）假设应急物流系统中，备选应急服务网点集为S=｛S1,S2,…,Sn｝,Sj（j=1,2,…,n ）为可能的应急服务网点，应急需求地点集为 F=｛F1,F2,…,Fm｝， Fi（i=1,2,…,m ）为应急需求地点。考虑在S个备选应急服务网点中选择p个建立应急物流中心，负责处理突发事件影响范围内应急物资的配送和分发。

（2）为了更好地表现实际情况，假设如果某备选应急服务网点被选中，则建设和经营该服务中心的固定费用已知。

（3）由于应急救援时间受交通因素的影响，假设从应急服务网点到应急需求地的最短时间是随机变量的分布函数。

（4）考虑各个应急需求地发生事故或灾害的等级不同，需要应急服务网点的数目也不同，假设对于应急需求地Fi，如发生事故时，需要能在规定的应急限制期ti到达的应急服务网点数至少为bi。

1.3 目标函数与约束条件

在应急救援时间为随机分布函数的限制条件下，设计相应的应急物流系统的目标为系统总费用最小，且在规定应急限制期内能够达到的应急服务网点数目满足一定要求。根据以上基本假设与限制条件，上述问题可转化为以下集合覆盖数学模型：

式中 决策变量：

常数：

cj——建立和经营Sj处应急服务网点的固定费用ti——从应急服务网点到应急地Fi之间的时间上限γi——应急需求地Fi所需要的服务水平

此模型目标仍为应急物流系统总费用最小，同时结合实际考虑满足在规定应急限制期内能够达到的应急服务网点数目要求。其中约束 （2）保证应急系统中，如果应急需求地Fi发生事故，则能在规定的应急限制期ti到达的应急服务网点数至少为bi；约束 （3）保证应急服务网点满足应急需求地对应急服务水平的限制。

1.4 基于贪婪启发式的求解算法设计

为方便求解首先定义：对于任意的Fi∈F，称Ni=｛j|tij≤t,j=1,2,…,n ｝为可供应急需求地Fi的服务集。

算法设计过程如下：

（1） R=M,S=Ø,t=1,Ni=｛j∈ N :aij=1｝（i∈M ） ；

（3） 对于 i∈M， 如果则∀j=Ni， Xj=1， S=S∪｛j ｝， bi=bi－aij。 如果 bi≤0， 则 R=R－ ｛i｝， 对于所有i∈R， 计算

（4） 如果 R=Ø， 转 （6）， 否则转 （5）；

（6）将S中的元素按照cj降序排列，依次取出j∈S，如果对所有i∈M，bi+aij＜1，则令bi=bi+aij，S=S－｛j｝，则S为最优解。

2 对给定限制条件下应急服务网点选址模型的改进

2.1 问题提出

在上一节中应急物流服务网点选址模型讨论中，仅仅局限于对应急时间规定一个限制期，然后把问题转化为典型的集合覆盖集问题。但是实际应对突发事件中，常常很难规定一个确定的应急限制期。同时，应急系统的决策者在进行系统选址决策时，还应充分考虑应急需求不确定性对选址问题的影响。故将给定限制条件的应急服务网点选址模型进行改进，即仍以系统费用最小为目标函数，但在原有模型的基础上改进应急时间约束条件，将其设为三角模糊函数，并引入应急需求随机变量因素，以使应急服务网点选址问题更具一般性。

2.2 基本假设与限制条件

（1）假设应急物流系统中，备选应急服务网点集为S=｛S1,S2,…,Sn｝， Sj（j=1,2,…,n ）为可能的应急服务网点，应急需求地点集为F=｛F1,F2,…,Fm｝， Fi（i=1,2,…,m ）为应急需求地点。考虑在S个备选应急服务网点中选择p个建立应急物流中心，负责处理突发事件影响范围内应急物资的配送和分发。

（2）为了更好地表现实际情况，假设如果某备选应急服务网点被选中，则建设和经营该服务中心的固定费用已知；同时在应急物流系统设计时，为满足决策者对备选应急中心进行扩建和新建的需求，假设备选应急服务网点中无容量和流量限制。

（3）由于应急需求地的需求变量和运输时间具有受多个微小的、独立的随机因素影响，且每一个因素都不具有主导作用的特点，固假设各应急需求地需求为独立需求，且需求量及运输时间限制为相互独立的正态分布随机变量。

（4）突发事件发生时特别是地震、洪水等自然灾害事件，可能会毁坏甚至阻断事件影响范围内的运输道路或是造成交通堵塞，所以假设备选应急服务网点到给定应急需求地的配送和分发时间是在一定范围内的模糊变量。

（5）在进行模型建立时由于会模糊参数和随机参数的同时出现，导致模型目标函数及约束没有明确的意义，所以假设模型中同时出现的模糊和随机因素为模糊机会和随机机会的并存。

2.3 目标函数与约束条件

在需求随机和配送时间模糊的限制条件下，相应的应急物流系统设计目标为系统总费用最小。同时，还要在一定服务水平上满足各应急需求地对运输时间的要求。为此，在考虑需求随机、运输时间模糊和时间约束条件下确定选择那些备选应急服务网点进行建立。根据基本假设与限制条件，上述问题可转化为以下数学模型：

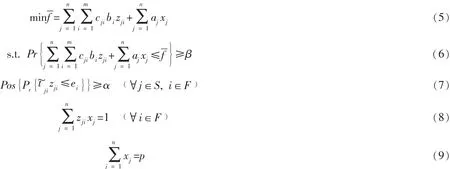
式中 决策变量：

常数：

aj——建立和经营Sj处应急服务网点的固定费用

bi——Fi需求地的独立需求量，为正态分布的随机变量

cji——从Sj选应急服务网点到Fi应急需求地的单位费用

~t——从Sj应急服务网点到Fi应急需求地的运输时间为三角模糊数

ji

ei——Fi应急需求地对运输时间的限制为正态分布的随机变量

p——配送网络所需应急服务网点数量

α和β分别为事先给定的对约束和目标的置信水平，Pos｛* ｝表示｛｝中事件的可能性，Pr｛* ｝表示｛｝中事件的概率。

此模型目标仍为应急物流系统总费用最小，同时考虑需求的随机和时间的限制，以及运输时间的模糊性。其中约束 （6）保证应急系统的建设和经营总费用期望值最小，并且概率不小于β；约束 （7）保证应急服务网点满足应急需求地对时间的限制；约束 （8）保证每个需求地只由一个应急服务网点提供应急资源；而α则可理解为应急物流系统满足应急需求地对配送时间限制。

2.4 基于模糊和随机模拟的遗传求解算法设计

遗传算法是一种很强的搜索和优化技术。它一般包括三个基本操作，即选址、交叉和变异。

基于模糊和随机模拟的遗传算法设计过程如下：

（1）定义整数pop-size作为染色体个数，并输入交叉概率Pc和变异概率Pm的值。

（2）输入参数pop-size的值，并在决策向量x的可行域中初始产生pop-size个染色体，用模糊随机模拟的方法计算染色体的可行性。

（3）使用模糊随机模拟的方法计算所有染色体的目标值，并将目标值由好到坏将染色体排序，且保留最好的目标值和染色体。

（4） 根据目标值， 采用基于序的评价函数eval（ Vi）=a（ 1-a ）i-1,i=1,2,…,m。pop_size对种群中的每个染色体Vi设定一个概率，以使该染色体被选择的可能性与种群中其它染色体的适应性成比例。

（5）根据交叉概率Pc和变异概率Pm的值，对选择的染色体进行交叉与变异操作，并使用模糊随机模拟方法检验后代的可行性。

（6）重复步骤 （3）到 （5），直到完成给定次数，将最好的染色体作为最优解。

2.5 实例验证

根据以上模型分析，采用仿真数据，进行模拟实验。

假设应急物流系统中，备选应急服务网点为S=｛S1,S2,S3,S4｝，应急需求地为F=｛F1,F2,F3,F4,F5｝，拟在4个备选应急服务网点中选者2个建立应急服务点，并要求以95%的服务水平满足5个应急需求地对时间和需求的限制，其中：

（1）建立和经营Sj（j= 1, 2,3,4 ）处应急服务网点的固定费用分别为 （单位：万元）：a1=30，a2=50，a3=19，a4=21；

（2） Fi（i=1,2,3,4,5 ）应急需求地的独立需求量bi为 （单位： 万件）：b1=（0.8 6 ,0.12 ），b2=（0.3 3 ,0.13 ），b3=（2.1 5 ,0.42 ），b4=（2.5 1 ,0.41 ），b5=（0.7 5 ,0.14 ）；

式中 bi为服从随机变量正态分布，分别表示第Fi地的需求期望值和标准差。

（3）从第Sj应急服务网点到第Fi需求地的单位运输费cji为 （单位：元/件）：

（4）从第Sj应急服务网点到第Fi需求地的运输时间为三角模糊数（单位：小时）：

（5） 第 Fi需求地对运输时间的限制 ei为 （单位： 小时）：e1=（3.0 1 ,0.13 ），e2=（3.1 5 ,0.24 ），e3=（2.8 0 ,0.11 ），e4=（2.5 2 ,0.12 ），e5=（3.2 1 ,0.21 ）； 式中ei为服从随机变量正态分布， μei和分别表示第Fi地对运输时间限制的期望值和标准差。

根据上节改进应急服务网点选址模型中设定的目标函数和约束条件，用Matlab编写基于模糊随机模拟的遗传算法程序，取种群规模pop-size=30，交叉概率pc=0.5，变异概率pm=0.05，基于序的评价函数为eval（ Vi）=0.05（ 1-0.05 ）i-1，目标置信水平β=0.96，运输时间的约束置信水平α=0.95，对模型进行计算，运行400代后得最优解为：

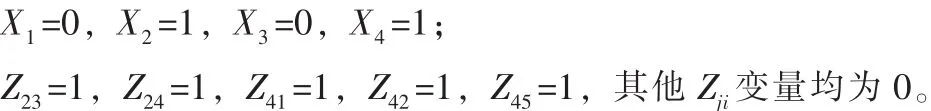
由计算结果可知，应建立第2备选应急服务中心，并向需求地3和4运输应急物资，同时建立第4备选应急服务中心，向需求地1、2和5运输应急物资，且2个应急服务中心可以以95%以上的服务水平满足5个应急需求地对运输时间和需求的限制，同时以不低于96%的概率实现应急物流系统最低成本的目标。

3 结束语

应急物流服务网点的合理选择能有效提高应急物流的服务水平，满足应急需求地对时间和需求的限制要求，最大可能的减少灾害损失，为害后恢复提供有力的保障。因此，应急物流服务网点选址模型的研究对于实现应急物流具有重要参考价值。

[1] 何建敏，刘春林，曹杰,等.应急管理与应急系统[M].北京：科学出版社，2005:68-75.

[2] 王晶，张玲，黄钧,等.基于不确定需求的鲁棒应急物流系统[J].数学的实践与认识，2009(10):53-60.

[3] 刘海龙.不确定环境下的物流中心选址问题研究[D].哈尔滨：哈尔滨理工大学，2007:17-20.

[4] 彭锦，刘宝碇.不确定规划的研究现状及其发展前景[J].运筹与管理，2002(2):1-9.