以均衡为目标的车辆调度问题研究
2010-07-24孙有望宋华骏同济大学交通运输工程学院上海201804
孙有望, 宋华骏 (同济大学 交通运输工程学院,上海 201804)
0 引 言
车辆调度问题 (VRP)一般定义为:对一系列发货点和收货点组织适当的行车路线,使车辆有序的通过它们,在满足一定的约束条件下 (如货物需求量、发送量、交发货时间、车辆容量限制、行驶里程限制、时间限制等),达到一定的目标 (如路程最短、费用最小、时间尽量少、使用车辆数尽量少等)[1]。它是一个复杂的组合优化问题,其中配送线路的调度为多目标决策问题,且属于NP-Hard问题[2]。
传统的物流企业拥有自己的车队,这些企业需要支付司机工资以及与车辆有关的一切费用,因而以往的车辆调度模型以行驶总里程最短为目标函数[3],或者以行驶总里程与固定费用总和最小为目标函数[4]。这些物流企业存在着工作量严重不均衡的现象,有的线路吃不饱,有的线路却任务繁重,这影响了司机的工作热情和满意度[2]。
目前,一些国内物流企业的发展已经颇具规模,他们将不同车型的车辆承包给司机,由此不再支付司机工资与车辆有关的任何费用,而仅仅在需要调度车辆时支付给司机出车费,以此获得更大的利润。因此,这些企业需要根据顾客的需求和车辆的相关信息,以总费用最低为目标选配车辆。本文将车辆调度问题分成两个阶段,第一阶段设计Ak-First Fit混合算法进行车辆选型,第二阶段针对不同线路工作量不均衡问题提出单位运输费用概念,建立新的目标函数并运用遗传算法 (Genetic Algorithm,GA)进行车辆路径优化。
1 问题描述和模型构建
1.1 问题描述
配送中心0需要向区域内的n个客户配送货物,各客户需求点的需求量为gi(i=1,2,…,n )。配送中心可调度h种不同车型的车共r辆型车辆的可调度数),s型车辆的最大载重量为qs,出车费用为Cs。各个需求点之间及需求点与配送中心之间的距离dij为已知。配送车辆从配送中心出发,沿着一条行车路线把所有货物送到指定位置后,返回自己所在的配送中心。且有 (sl表示s型车辆的第l辆车):

1.2 模型构建
根据司机承包车辆以及均衡各线路工作量的物流管理理念将车辆调度问题分解为一个车辆选型问题P1和一个车辆路径优化问题P2。

其中ms为s型车辆的调度数。式 (1)表示s型车辆的调度数不能大于该车型的可调度车辆数,式 (2)表示每个需求点有且仅有一辆车进行配送。
由于线路工作量主要取决于送货里程和送货量,因此引入单位运输费用概念csl,即将s型车辆的第l辆车的出车费用Cs除以该车的送货量以及该车的送货里程当所有车辆的单位运输费用接近时,所有线路的工作量亦接近,模型如下:
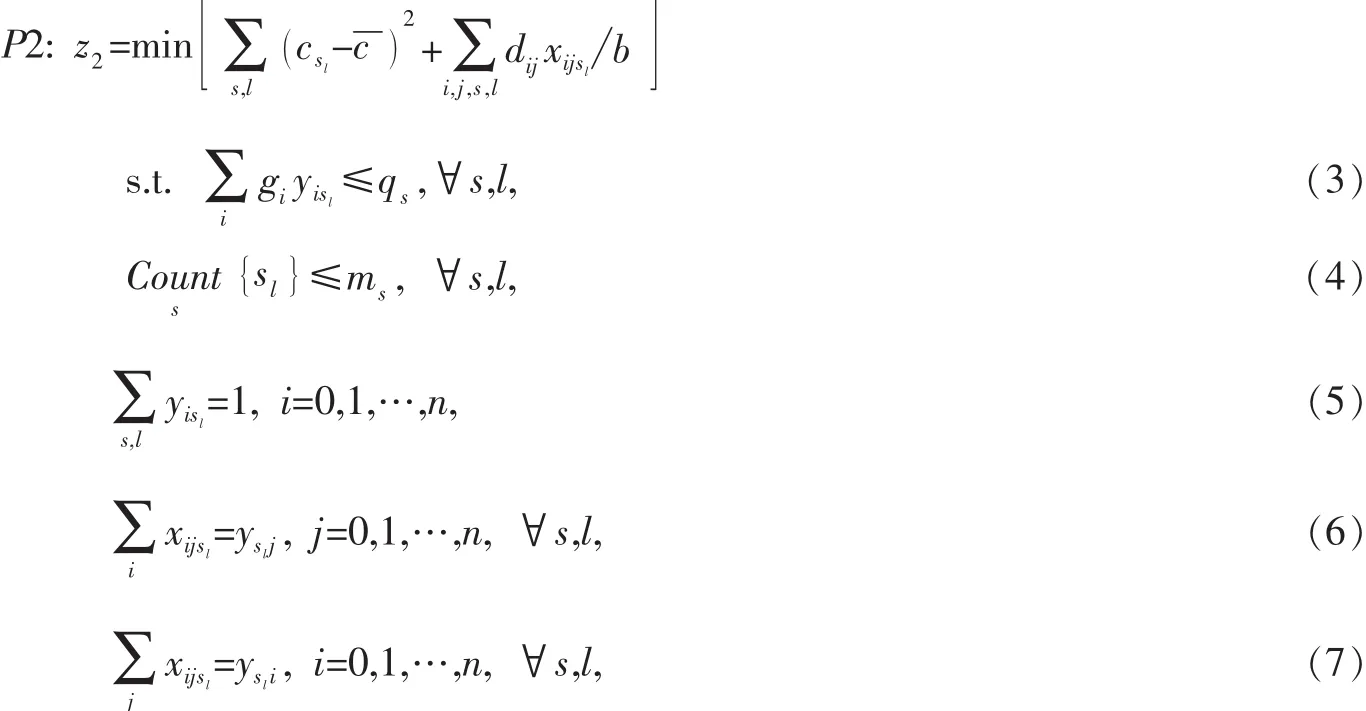
P2的目标函数综合考虑了配送线路总里程数以及单位运输费用方差。其中b为常数,当b取值较小时,目标函数主要决于配送线路总里程数,此时更强调配送效率,而当b取值较大时,则目标函数主要取决于单位运输费用方差,此时更强调线路作业量的公平性。sl表示s型车辆的第l辆车,表示平均单位运输费用。式 (3)表示每辆车的装载量不能超过其最大载重量,式 (4)表示s型车辆的出车数不能大于P1求得的调度数,式 (5)表示每个需求点有且仅有一辆车进行配送,式 (6)、 (7)说明对于每个客户i,只有2个客户与i相连,车辆由一个客户直接驶向它,又由它直接驶向另一个客户。
2 算法设计
2.1 车辆选型Ak-First Fit混合算法
Ak-First Fit算法是一种混合启发式搜索算法,算法的基本思想是:首先从全部r辆车中选出k辆车,按客户需求量的非递减次序将每一个需求点的货物装入第一辆可以装得下的车,直至k辆车全部装满,然后按车辆出车费用从小到大的次序挑选车辆,根据前述原则继续装载货物,直至所有的货物都装载完毕为止。算法的主要步骤如下:
输入: (C1, C2,…,Ch)及 (n1,n2,…,nh)和 (g1,g2,…,gn)
输出: (m1,m2,…,mh)和出车总费用z1
Step1: 构造集合 (C11,C12,…,C1n1,C21,C22,…,C2n2,…,Ch1,Ch2,…,Chnh), 并将其按非递减次序排序, 设排序后结果为集合N
Step2:对集合 (g1,g2,…,gn)按非递增次序排序,设排序后结果为集合M
Step3: 令 m1=0,m2=0,…,mh=0,z1=∞
Step4:从N中生成第一个元素个数≤k的子集T作为初始车辆集
Step6:从集合T中选择第一辆装得下集合M中第一个元素{gi}的车辆,若该车辆存在,则令M=M{gi},转Step6,若该车辆不存在,则转Step7
Step7:若M≠φ,则从NT集合中选取第一个元素Csl,若该元素存在,则转Step8,否则说明原问题无可行解,停止计算
若M=φ,则转Step9
Step8: 令T=T∪{sl},tempms=tempms+1,tempz1=tempz1+Cs, 转Step6
Step9:若tempz1≤z1,令z1=tempz1,ms=tempms,否则转Step10
Step10:若能生成下一个元素个数≤k的子集T,则转Step4,否则,若不能再生成下一个元素个数≤k的子集T,则输出: (m1,m2,…,mh)和z1
2.2 车辆路径遗传算法
2.2.1 遗传算法编码设计
采用自然数编码,各种车型的车辆数ms由P1求得,自然数n表示客户的个数,染色体结构表示为:(0,i11,1,i112,…,i11t,0,i121,i122,…,i12u,0,…,0,ihmh1,ihmn2,…,ihmhv), 染色体的总长度为其中,自然数islj表示s型车辆的第l辆车路线中的第j个客户,自然数0表示配送中心,m个0把染色体分为m段,代表m条路径。
2.2.2 种群的初始化
产生初始群体的步骤如下:
Step1:为保证模型一定有可行解,将P1阶段由Ak-First Fit混合算法求得的车辆配送路径直接加入初始种群
Step2:产生随机客户序列,如 (3,5,n,…,l),将配送中心0插入该序列第一个位置
Step3:从第一个客户点开始向后搜索,逐次累加客户需求量。当新加入一个客户点,已累加需求量大于车辆最大载重量时,则在该客户点之前插入0,并重新开始累加客户需求量。共需插入构成长度为n的一条染色体,先插入的0代表载重量较大车型的起点。为了防止产生无效的染色体,插入0后满足任意两个0不相邻
Step4:重复Step2-Step3,直至满足种群规模size
2.2.3 适应函数值计算
对于算法迭代过程中每代个体的优劣通过个体适应函数值进行评价。对违反约束条件的个体引入惩罚值函数,以确保那些符合约束条件而较优的个体有较大的生存机会。
该指标可综合反映染色体配送线路总里程数及单位运输费用方差。
overload为0表示车辆调度方案满足车辆最大载重量约束时,个体适应函数值为原值,overload为1表示车辆调度方案超载时,个体适应函数分母需加上惩罚值,C为惩罚值。
2.2.4 选择
采用改进的轮盘赌选择法。选择过程中将群体中适应函数值最大的个体直接复制到下一代,对于其他个体,其被选择的概率为:
p(i)等于第i条染色体的适应度在整个群体的适应函数值总和中所占的比例,染色体的适应函数值越大,则其被选中的概率越高。
2.2.5 交叉
遗传算法思想的核心之一是在进化过程中,子代能够充分继承父代的优良基因,并且有所发展,可谓扬弃。如果单纯得使用一般的交叉算子往往会使一些优秀的子路径被破坏,并且在两个父体相同时,无法再产生新的个体。这里采用对顺序交叉 (OX)方式进行改进的一种交叉算子[5]:
首先通过随机函数产生两个数作为交叉点,两个父个体交叉时,通过选择父个体1的一部分,然后保存父个体2中的客户码的相对顺序生成。
例如:对下面两个父个体,随机选择两个数(3,9 )作为交叉点:

首先,将两个交叉点之间的中间段和第一位的基因码保留,得到:

然后取f2从第2个交叉点开始的客户码排列顺序,当到达表尾时返回表头继续记录客户码,直到第2个交叉点结束,得到客户码排列顺序 (0 4 5 0 3 7 8 1 0 62 )。将o1中拥有的客户码从该排列顺序中去掉,可得排列顺序(7 8 16 ),将这个排列顺序复制给o1,复制的起点从第2个交叉点开始,得到交叉后的客户码排列顺序o1:(0 6 3 0 5 2 0 4 7 81 ),同理可得o2: (0 4 7 8 1 0 6 2 3 50 )。
2.2.6 变异
采用有条件变异算子,以防止种群退化。当染色体适应值大于a时,不进行变异,否则据概率pm对染色体进行基因换位变异。
2.2.7 算法的实现过程
Step1:令迭代次数k=0,确定算法的最大迭代次数K、种群规模size、交叉概率pc和变异概率pm
Step2:产生初始种群,计算群体中所有个体的适应函数值fk,找出适应函数值最大的染色体
Step3:若k=K,则转Step6,否则转Step4
Step4:将群体中最优的个体直接复制到下一代,按照概率p(i)、pc和pm分别选择个体进行选择、交叉和变异操作
Step5:计算子代个体的适应函数值fk,令k=k+1,转Step3
Step6:输出最优结果,适应函数值fk最大的个体为算法的最优个体,解码得到最优车辆路径
3 结束语
针对新的物流管理理念提出两阶段模型,实例计算表明该模型能够兼顾效率与公平。对于拥有自己车队的物流配送企业,不论是否拥有多种车型,该两阶段模型仍然适用。但是模型中各项初始参数的设定会影响算法的收敛性、收敛速度和计算时间,因此需要通过在实际问题中进行大量的数值模拟,从中选择比较理想的参数搭配,才能最大限度地提升运行效率。
[1] 贾永基,谷寒雨,席裕庚.一类货运车辆调度问题的混合禁忌搜索算法[J].信息与控制,2006(33):724-728.
[2] 曹二保,赖明勇,聂凯,等.大规模物流配送车辆调度问题研究[J].湖南大学学报:自然科学版,2007,34(12):89.
[3] 张海刚,顾幸生.基于DNA进化算法的车辆调度问题[J].华东理工大学学报:自然科学版,2006,32(12):1464.
[4] 朱永亮,王金妹.物流配送车辆路线求解算法[J].交通运输工程学报,2006,6(2):85.
[5] 朱连章,张红霞.基于着色Petri网的电子商务工作流建模[J].中国石油大学学报,2006,30(4):141-144.
