基于确定当量的风险规避零售商最优订货决策分析

邓景毅，张小康 DENG Jing-yi,ZHANG Xiao-kang

（1.暨南大学 管理学院，广东 广州 510632；2.广东商学院 信息学院，广东 广州 510320）

供应链是由供应商、零售商及用户构成的网络，其目的是实现整体最优，避免因局部理性造成的全局效率下降。在供应链网络上的各实体之间建立契约关系是的重要手段之一，包括批发价格契约、数量弹性契约、收入共享契约、销售回扣契约、回购契约等[1-5]。目前，大部分的供应链契约理论都是以报童模型为基础，并且进一步发展该模型。报童模型的假设之一是：供应链实体 （agent）是风险中性的——各实体的目标是收益最大化。但是，现实中的实体并不都是风险中性的，它们可能存在各种风险偏好，既可能是始终规避风险或者趋向风险的，也有可能是在收益低时趋向风险而收益高时规避风险。不少文献对实体风险偏好进行了研究，其中既有对供应链中的单个实体决策进行研究的成果 （如文献[7,8,12]等），也有对整个供应链中存在风险偏好实体时如何进行协调的研究成果 （如[9,15]等）。其中，Lau等 （1999）应用方差，对原有的收益函数进行修正，进而确定供应商的定价策略[7]。Agrawal等 （2000）研究了价格随需求发生变化的风险规避零售商的订货决策问题[8]。Gan等 （2004）则在原有的收益函数基础上，将方差作为求解最大收益的约束条件，探讨了风险规避实体的供应链协调问题[9]。国内不少学者也在供应链的风险研究方面作了有益的探索，包括叶飞 （2006）和于春云 （2007）等[10-11]。总的说来，对单个实体风险偏好研究较多，而对整个供应链的风险偏好问题研究的较少 （或者说是：供应链中包含一个或者多个风险偏好实体的协调问题），但前者是后者的基础。在批发价格契约基础上建立的报童模型，风险主要由零售商承担。因此，本文以供应链中零售商的订货决策为主要研究对象。

1 问题的提出

不论是研究单个实体的风险偏好还是研究整个供应链在风险偏好下的协调问题，供应链实体风险偏好研究的核心在于：应用何种风险度量模型以何种方法对实体的风险偏好进行处理。归纳目前的文献，采用的风险度量模型包括：均值－方差模型、指数模型、CVaR模型等；风险对实体决策的影响处理方法包括：最大效用法[12]、确定当量方法、约束条件法、收入函数修正法等。最大效用法直接应用效用最大化为依据进行决策，该方法的决策结果直接与选取的效用函数相关，还与效用的初始值等因素相关[12]。约束条件法要求收益方差不大于某一方差阈值δ，但是从文献[8,10]等可以看出，该方差是一个绝对值，它的大小取值与收益的大小是相关的，即收益大时，即使方差较大也可能被风险规避者接受。因此，在实际应用中，阈值δ的取值较难确定。收入函数修正法也采用方差进行分析，所不同的是其将δ与系数k相乘后直接代入收益函数进行分析[7]，该方法中，系数k的取值与风险偏好相关，但是其取值的逻辑依据以及k是否是一个常数值得商榷。

确定当量法由Simon和Theil提出，用于动态理性期望模型分析，其在资本预算领域中广泛采用，是进行风险处理的有效方法[13－14]，在文献[14]中对确定当量法的应用进行了详细描述。确定当量法的优点在于引进风险偏好的同时，仍然采用收益最大法进行决策分析，这样就保证了与风险中性分析的一致性，便于比较研究；而且，其采用的当量处理可以部分减少效用函数选取对决策值的影响 （通过取效用函数的反函数实现），而保留风险偏好的影响，因此它是一种较好的风险研究方法。利用确定当量法处理供应链风险问题在国内尚未见到相关文献。本文采用指数效用模型对风险进行定量，利用确定当量法对风险进行处理，并且数学证明了，风险规避将使得零售商订货量下降；风险规避系数越大，订货量下降越多。通过数值实验，比较了不同风险规避系数下，零售商的最优订货量。

2 模型的基本描述与构造

考察由一个供应商和一个零售商组成的二阶段供应链系统。供应商提供单一商品，在销售季节开始前，零售商下达订货单，供应商收到订单后组织生产并且发货。零售商在每个销售季节开始前只有一次订货机会，向供应商提交订货数量Q，中间不能补充订货。市场需求D是一个非负、连续型的随机变量，其分布函数为F（x ），密度函数为f（x），并且满足IGFR条件 （Increasing Generalized Failure Rate，正态分布、指数分布、威布尔分布等均满足该条件）。供应商依据订货量进行生产，生产成本为c，并且以批发价格w出售给零售商。零售商在获得商品后将再次出售，售价为p，p＞w＞c。若商品在该销售季节内未被出售，其残值为v，c＞v。为简化模型，不考虑缺货成本，这意味着供应链的风险全部由零售商承担，而供应商不承担风险。

根据已知条件，分析可知，供应商的收益为：

零售商的收益为：

供应链的收益为：

在满足供应链收益最大的条件下，对 （3）求导，可得：

其中， F－1（·）是F（x）的反函数，Q*是供应链收益最大时订货量的取值。

2.1 风险中性下，零售商的订货决策

当零售商为风险中性时，零售商的决策依据是收益最大化，即 （2）式取最大值。 （2）式对Q求导，可以得到：

由于增函数的反函数也是增函数，所以，可对式 （5）进行变换可得：

由 （6） 式和 （2） 式，可以得到：

对 （7）式求导，得到：

由上式可知，在风险中性下，零售商的利润随着订货量的增加而增加。

由 （6） 式和 （3）式可以得到：

文献[3]利用价格弹性证明了式 （9）是单峰的，πsn存在最大值，此时

2.2 风险规避下，零售商的订货决策

指数效用函数是在处理风险和效用问题时常用的经济学模型。假设零售商具有如下的效用函数：

k＞0，称为风险规避因子，k越大，实体对风险越厌恶；R表示收入。由于U'/U"是一个常量，因此，在U的有效定义域内，实体对风险的容忍程度保持不变。

由（2）式可知，当市场需求在x∈[0,Q)时，零售商的收入可以表示为：p－（）v x；当市场需求在x∈[Q,+∞)时，零售商的收入可以表示为：p－（）v Q。因此，零售商的期望效用可以表示为：

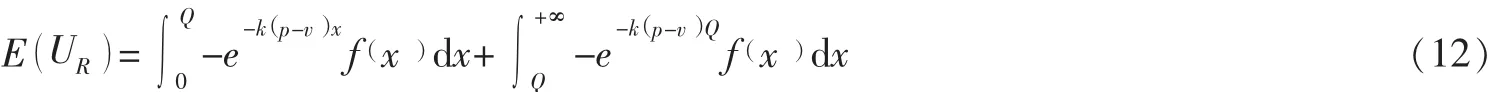
由 （2）式和 （13）可知，风险规避零售商的收益为：

对风险规避零售商的收益函数取最大值，可以得到，此时的最优订货量为：

（15）的存在性证明见下文。

对于 （14）式，进一步分析可以得出以下结论。

命题1对于给定的w，风险规避零售商的收益为凹函数。

证明：式 （14）对Q取一阶和二阶导，可得：

命题得证，也就证明了 （15）式成立。

命题2对于给定的w，Qa＜Qn。

证明：若Q＝0，显然对于式 （16）有：

对于给定的w，风险中性零售商的最优订货量Qn满足式 （5）。由式 （5）和式 （16）得到：

依据式 （17）、 （18）、 （19） 式以及拉格朗日中值定理可知， 在 ［0, Qn］之间存在Qa使得 πra取最大值。 因此，风险规避零售商将选择较风险中性零售商更小的订货量，这符合实际，与直觉吻合。同时，也从侧面证明了模型的合理性。

命题3对于不同的风险规避因子k1,k2，若存在k1＜k2，则它们所对应的最优订货量存在如下关系：其中表示风险规避因子为ki时的零售商最优订货量。

变换可得：

式 （21）对k求导，可以得到：

3 数值实验

表1 不同批发价格下，Qa和Qn的比较

图1 最优订货量随批发价格的变动

由图1可看出，风险规避零售商的最优订货量较风险中性零售商的订货量小，两者之间的差值随着批发价格的上升而下降。这一现象可以将市场需求的密度函数带入式 （16）而得到数学上的解释。更为直观的解释是：由于批发价格的上升，Qn和Qa均减小，但是由于Qn是风险中性下的订货量，其减小的速率更快些，从而使两者的差值及其比率越来越小。

当批发价格确定时，零售商的订货量将随着风险规避因子的变化而发生变化，见表2和图2。

由图2可以看出，随着风险规避因子的不断增加，零售商的订货量不断减少。当w=4时，如果风险因此由0.05上升至0.45，订货量Qa下降超过50%。而根据负指数效用函数理论，当风险规避因子达到0.45时，已经对风险相当厌恶了。同时，也可以发现，w越小，曲线的曲率越大，说明在w较小时，风险规避因子对订货量影响比较大。

表2 风险规避因子对Qa的影响

4 总 结

模型的作用在于简化系统内部各要素之间的联系，以便于分析问题，抓住事务的主要矛盾。建立模型后，应该不断对模型进行修正，以使得模型能够更好的预测现实世界。风险中性假设与现实并不吻合，将风险因素引入供应链模型是必要的。负指数效用函数在风险定量研究中有着广泛的应用。通过确定当量法，将期望效用值转化为确定效用值，从而将风险因素引入零售商收益函数进行分析和处理，进而计算出零售商的最优订货量这是一种有效供应链分析方法。供应商在确定零售商为风险规避者时，将如何进行决策是我们进一步的研究方向。

[1]B.Pasternack.Optimal Pricing and Returns Policies for Perishable Commodities[J].Marketing Science,1985(4):166-176.

[2] A.Tsay.Quantity-Flexibility Contract and Supplier-Customer Incentives[J].Management Science,1999,45(10):1339-1358.

[3] Selling to the Newsvendor.An Analysis of Price-Only Contracts[J].Manufacturing&Service Operations Management,2001,3(4):293-305.

[4] T.Taylor.Supply Chain Coordination under Channel Rebates with Sales Effort Effects[J].Management Science,2002,48(8):992-1007.

[5]P.Cachon,A.Lariviere.Supply Chain Coordination with Revenue-Sharing Contracts:Strengths and Limitations[J].Management Science,2005,51(1):30-44.

[6] G.Perakis.The Price of Anarchy in Supply Chains:Quantifying the Efficiency of Price-Only Contracts[J].Management Science,2007,53(8):1249-1268.

[7] H.Lau,A.Lau.Manufacturer’s Pricing Strategy and Return Policy for a Single-Period Commodity[J].European Journal of Operational Research,1999(116):291-304.

[8] V.Agrawal,S.Seshadri.Impact of Uncertainty and Risk Aversion on Price and Order Quantity in the Newsvendor Problem[J].Manufacturing and Service Operations Management,2000,2(4):410-423.

[9] X.Gan,S.P.Sethi,H.Yan.Coordination of Supply Chains with Risk-Averse Agents[J].Production and Operations Management,2004,13(2):135-149.

[10] 叶飞.含风险规避者的供应链收益共享契约研究[J].工业工程与管理，2006(4):50-53.

[11] 于春云,等.具有风险规避者和偏爱者加盟的供应链优化与协调模型[J].系统工程，2007,25(1):13-20.

[12] L.Eckhoudt,C.Gollier,H.Schlesinger.The Risk-Averse （and Prudent） Newsboy[J].Management Science,1995,41(5):786-794.

[13] L.P.Hansen,T.J.Sargent.Certainty Equivalence and Model Uncertainty[C]//Board of Governors of the Federal Reserve System Proceedings,2005:17-38.

[14] R.L.Keeney,H.Raiffa.Decisions with Multiple Objectives:Preferences and Value Tradeoffs[M].Cambridge University Press,1993.

[15] V.Agrawal,S.Seshadri.Risk Intermediation in Supply Chains[J].IIE Transactions,2000(32):819-831.