车辆数不确定的时间窗车辆路径问题的小生境混合遗传算法

程松山，杨 涛 CHENG Song-shan,YANG Tao

车辆路径优化问题 （Vehicle Routing Problem，VRP）最早是由Dantzig[1]提出的，是现代物流系统中关键的一环。时间窗的车辆路径问题 （Vehicle Routing Problem with Time Window,VRPTW）是对简单车辆路径问题（VRP）的进一步扩展。目前，国内外关于VRPTW的研究很多，如Braysy O[2]、KIT M[3]、Joe[4]、李军[5]和朗茂祥[6]等。本文提出一种基于小生境的改进的混合遗传算法，采用并行选择法构造Pareto解以及精英保留策略，从而克服了遗传算法搜索速度慢、局部搜索能力差以及 “早熟”的先天性不足。

1 数学模型

1.1 VRPTW问题描述

假设中心仓库有k辆载重均为Q的车，为n个等待客户服务，已知仓库中心和每个客户端位置坐标、客户的货物需求量和允许的服务的时间窗口以及服务时间。试寻求最优的车辆配送路线，使得分派到车辆数最少，且配送过程中的总行驶路程最短。

1.2 数学模型

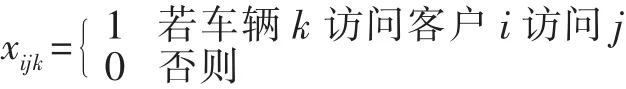
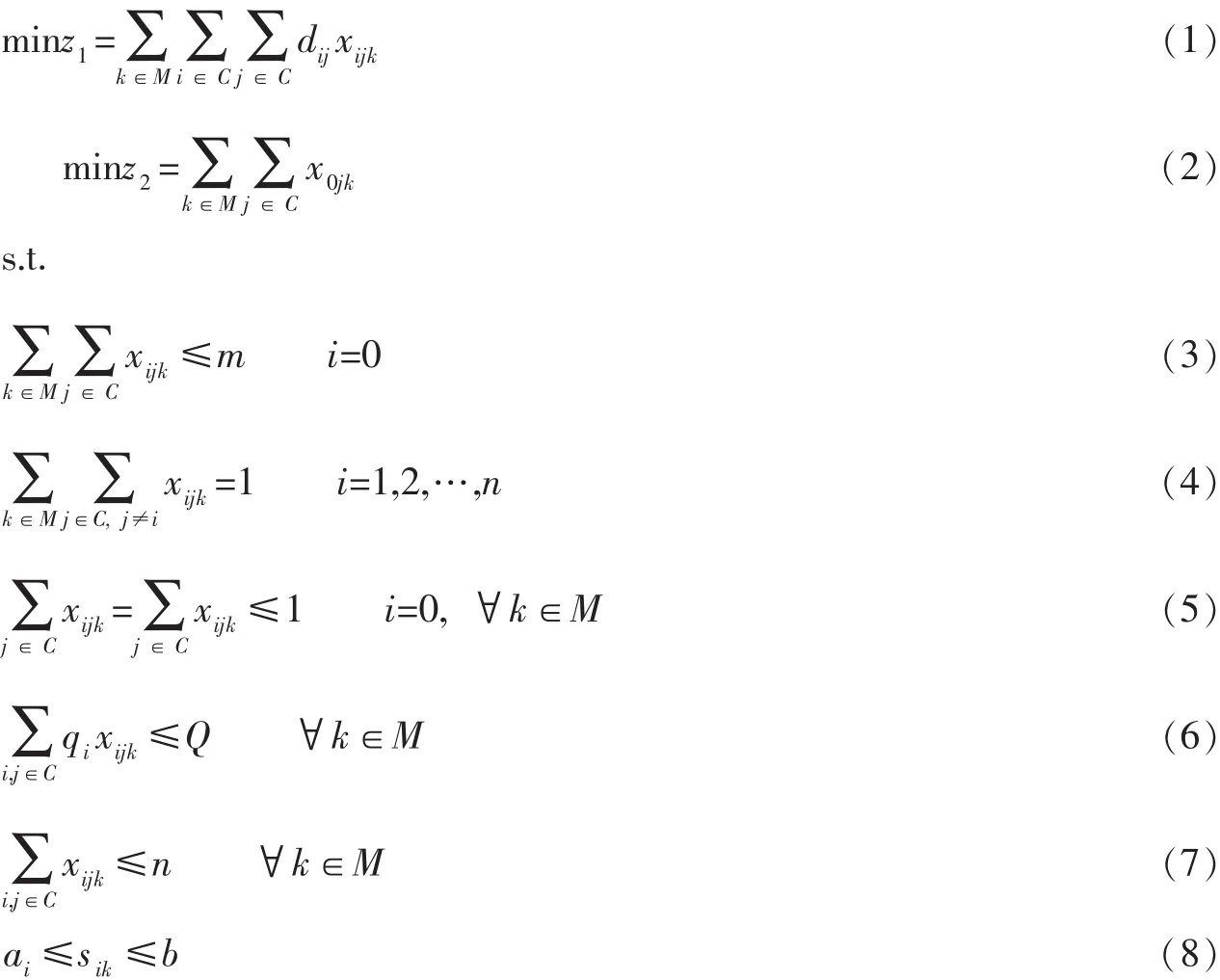
式中：M为车辆数目集，M=｛k=1,2,…,m ｝，m是一个待定的决策的变量；C为客户集，C=｛i,j=1,2,…,m ｝，i,j=0时为中心仓库；dij为客户i与客户j之间的距离；qi为客户i的需求量；sik为车辆k到达客户i的时间；si为车辆在客户i处的服务时间。

式 （1）表示总行车路程最短；式 （2）表示指派最少的车辆；式 （3）表示从中心仓库出发点车辆数不能超过故有的车辆数m；式 （4）表示每一个客户只能有一辆车辆服务且每个客户均能得到服务；式 （5）表示保证车辆从中心仓库出发并最终回到中心仓库；式 （6）表示每辆车辆运送的货物重量不能超过车辆的定额载荷；式 （7）表示每辆车服务的客户总数不能大于客户总数目；式 （8）客户i允许的服务时间窗口。

2 算法设计

2.1 染色体的编码方式及初始群体的生成

本文染色体采用自然数编码方式。即染色体V=｛vi｝（i=1,2,…,n ），vi表示染色体的基因，对应于第i个客户的编号，如，V=｛4,2,5,3,1 ｝就是一条染色体。染色体中没有路线分界点的基因位。

初始群体个体初始化的方法是前相插入法，生成一个好的可行个体，然后在此个体的邻域内生成部分个体，这些个体数占初始群体规模的十分之一，余下的十分之九的个体随机产生。

2.2 适应函数的构造

本文适应函数的构造采用Murata，Ishibuchi和Tanaka提出的随机权重法 （random-weight approach）[7-8]。该方法能够使得遗传算法具有可变搜索方向，在整个Pareto前沿面上进行均匀采样的能力。

设最小化的q个目标函数，权重和目标 （weighted-sum objective）如下所示：

其中fk（）x=zk,k=1,2，随机权重wk由下式计算：

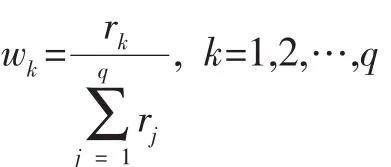
其中ri是非负随机数。

但是式 （9）实际存在问题，那就是fk（x）之间的单位不统一，而且两者之间的数据相差几十倍，这样如果不将其进行改进，f1（x）的量有可能将f2（x ）的量 “淹没”，这样就会导致f2（x ）这个目标值名存实亡。鉴于此，本文将其改进为：

其中fkmax（x）是每一代过程中种群最大值。

2.3 交叉操作

首先随机地在染色体串中选择一个交叉区域。如两父串及交叉区域为，A=1|234|5，B=2|341|5，然后将B的交叉区域放到A的最前面，将A的交叉区域放到B的最前面，分别得到A′=34112345，B′=23423415，最后分别在A′和B′中最交叉区域后依次删除与交叉区域相同的点，得到最终交叉后产生的两个新染色体，A′=34125，B′=23415。该方法对维持种群的多样性有较好的作用。

2.4 变异操作

传统的均匀操作不便于对某一重点区域进行局部搜索，其局部操作能力较差，故本文采用非均匀变异操作[9]。在进行由V=v1v2…vk…vp向的非均匀变异操作时，若变异点vk的基因值取值范围为则新的基因值由下式确定：

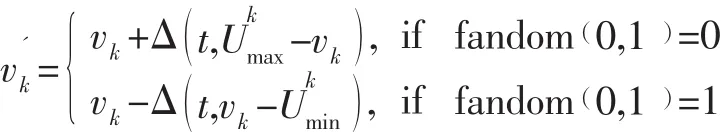
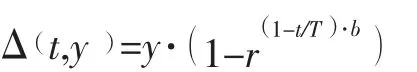
式中t是循环变量，T是最大进化代数，b是一个系统参数，决定算法的收敛压力，r是一个0,（）1内均匀产生的随机数。

2.5 混合并行遗传算法

多目标优化问题的遗传算法的选择操作有并列选择法、排序选择法和共享函数法等多种方法。各种方法都有自己的优缺点[9]，鉴于此，本文混合使用上述几种求解多目标优化问题的方法，尽可能的克服各自的缺点，而充分发挥各自的优点。把它叫做混合并列选择法[9]，其选择过程如下：

（1）并列选择过程。按所求多目标优化问题的子目标函数的个数，将整个群体均等划分为一些子群体，各个子目标函数在相应的子群体中产生其下一代群体。

（2）保留Perato最优个体过程。在每一代的过程中，对于各个子群体中的Perato最优个体，不让其参与个体的交叉和变异运算，而是让其直接保留到下一代子群体中。这样可以避免因交叉和变异运算导致的破坏良好的染色体，加快其搜索速度。

（3）共享函数处理过程。若得到的Perato最优个体是数量已超过规定的群体规模，则需要利用共享函数法对最优个体进行挑选，以形成规定规模的新一代群体。

3 实例与分析

为了测试算法的有效性，分别采用文献[10-13]的5个典型问题进行了测试，并于目前已知的最好解进行了比较。

算法用Java语言编程，在PC586兼容机上运行。参数设置：种群规模M=100，最大进化代数为200，交叉概率pc=0.8，pm=0.001。计算最好目标值和最差目标值，然后计算平均值，测试结果如表1所示。以问题1（见表2）为例，给出所求最好解的各条路径。

从表1可见：

（1）在算法中采用非均匀变异，适应值的计算采用随机权重法，这样该算法在初始运行阶段进行均匀随机搜索，而在其后期运行阶段进行局部操作，使得该算法所得的解与已知最优解的偏差小，而且明显好于参考文献[14]的结果。

（2）小生境的混合并行选择法以及精英保留策略使得本算法有较高的运行效率和收敛性，使得解的质量和求解速度上都得到了提高。

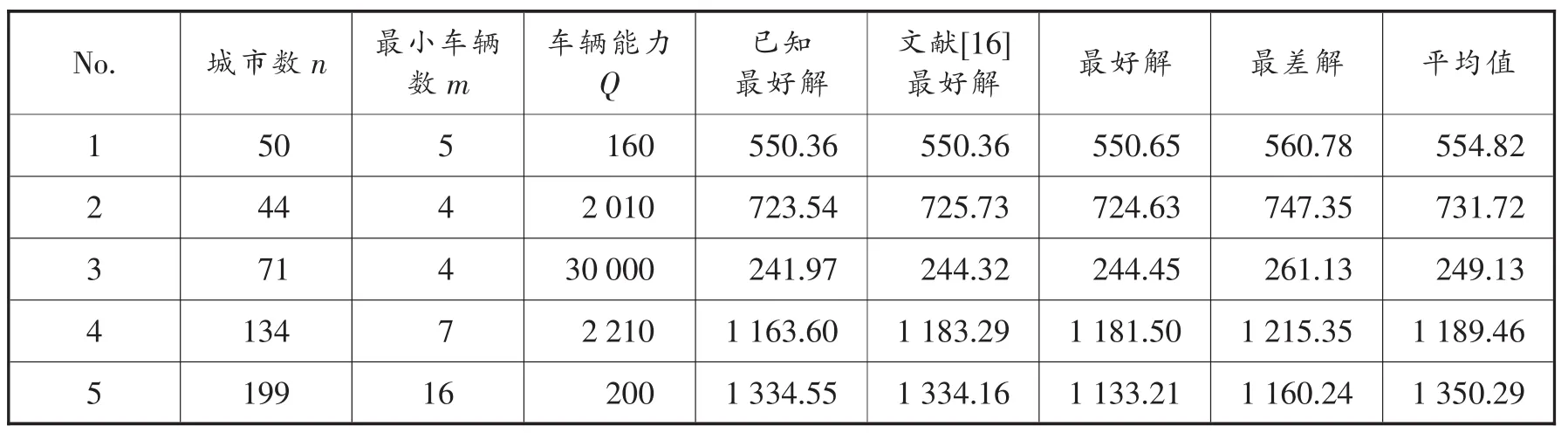
表1 测试结果

从表2中可以看出，各条路径中的车辆的装载率都比较高。因此本算法是有效的。

表2 n=50,Q=160

4 结 论

本文在描述问题模型的基础上，从多目标角度出发，针对传统的遗传算法存在的收敛速度慢、易早熟、局部搜索能力差等缺点，采用精英保留策略，引入自适应变异算子，并使用随机权重的适应函数，从而构造了一种基于小生境的混合并行选择法的改进遗传算法。仿真实验表明该算法对于解决车辆数不确定的时间窗车辆路径问题提供了一个非常有效的求解方法。

[1] Dantzig G,Ramser J.The truck dispatching problem[J].Management Science,1959(6):80-91.

[2]BRAYSY O,DULLAERTW,GENDREAUV M.Evolutionary algorithms for the vehicle routing problem with time windows[J].J Heu-ristics,2004,10(6):5872-11.

[3]KITM,HBR ID A.Genetic algorithm for the vehicle routing problem with time windows[J].International J on Artificial Intelligence Tools,2001,10(3):431-449.

[4] Joe L,Rover L.Multiple Vehicle Routing with Time and Capacity Constraints Using Genetic Algorithms[C]//Proceedings of the Fifth International Conference on Genetic Algorithms,1993:452-459.

[5] 李军，郭耀煌.物流配送车辆优化调度理论与方法[M].北京：中国物资出版社，2001.

[6] 朗茂祥，胡思继.用混合遗传算法求解物流配送路线优化问题的研究[J].中国管理科学，2003(4):51-56.

[7] Ishibuchi,H.,T.Murata.A multiobjective genetic local search algorithm and its application to flowshop scheduling[J].IEEE Transaction on Systems,Man and Cybernetic,1998,28(3):392-403.

[8]Murata,T.,H.Ishibuchi,H.Tanaka,Multiobjective genetic algorithm and its application to flowshop scheduling[J].Computers and Industrial Engineering,1994,72:417-431.

[9] 周明，孙树栋.遗传算法原理及应用[M].北京：国防工业出版社，1998.

[10] Marshall L Fisher.Optimal solution of vehicle routing problems using minimum K-trees[J].Operations Research,1994,42(4):626-642.

[11] Glover Fred.Tabu search-partⅠ[J].ORSA Journal on Computing,1989,1(3):190-205.

[12] Glover Fred.Tabu Search-partⅡ[J].ORSA Journal on Computing,1990,2(1):4-32.

[13] Christofides N,Eilon S.An algorithm for the vehicle dispatching problems[J].Operations Research,1969,20:309-323.

[14] 张涛,等.不确定车辆数的车辆路径问题模型和混合算法[J].系统工程理论方法应用，2002,11(2):121-130.