基于正则参数后验策略的PCS迭代正则化反演
2010-07-23王远磊王雅静朱新军
王远磊,申 晋,王雅静,朱新军,刘 伟
(山东理工大学电气与电子工程学院,山东淄博255049)
PCS(photon correlation spectroscopy光子相关光谱)技术是测量亚微米及纳米颗粒粒度及其分布的有效方法[1],其中粒度反演一直是PCS方法的难点[2].目前,反演算法主要有:累积分析法,双指数法,非负约束最小二乘法,CONT IN法等[3-7].累积分析法只适用于单峰颗粒的反演.双指数法对具有双颗粒分布的颗粒反演比较适用,但对于单峰或多峰分布不适用.非负约束最小二乘法难以应用于单峰颗粒反演.CONTIN法实际上是一种附加先验约束条件的约束正则化方法,先验策略是在求出正则解以前已将正则参数确定下来,这需要大量的先验材料,先验材料在实际中经常不确知.文献[3] 中实验测量表明CONTIN算法的分辨力较弱,其反演质量的提高依赖于恰当选择正则参数.喻雷寿采用迭代CONTIN算法进行反演[4],其方法是通过不断缩小反演区间进行反演,反演结果比CONTIN算法精确了很多,但计算量较大.韩秋燕采用正则参数后验策略的正则化方法,对单峰和双峰分布颗粒系自相关函数进行了反演[7],对于单峰的反演能够得到较准确的结果,当噪声大于一定水平时双峰的反演结果不理想.本文采用一种形式简单的迭代正则化方法—Tikhonov迭代正则化方法[8],反演区间不变,并采用改进的Morozov偏差原理选择正则参数,对单峰和双峰分布颗粒系的模拟电场自相关函数进行了反演.
1 PCS的基本理论
对随机的散射光信号进行相关运算并做归一化处理,得到多分散颗粒体系的电场自相关函数
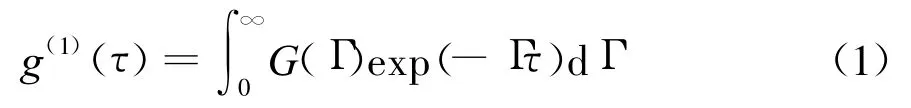
式中:τ是相关延迟时间;G(Γ)是归一化的衰减线宽的分布函数为衰减线宽,其中是Boltzmann常数,T代表绝对温度,η为溶液粘性系数,r为当量球型颗粒的流体力学直径,为散射波矢量,试中,n为溶液的折射率,λ。为激光在真空中的波长,θ为散射角.式(1)为第一类Fredholm积分方程,要从带有噪音的g(1)(τ)求解颗粒粒径属于病态问题(ill-posed problem),原始数据的微小扰动误差便导致解的严重偏离[2].
2 迭代正则化
要根据(1)式反演出颗粒粒径,首先把(1)式离散化得

式中A的元素Aij=exp(-τiΓj),其中τi对应相关器第i个通道延迟时间,Γj表示离散化后第j级衰减线宽.
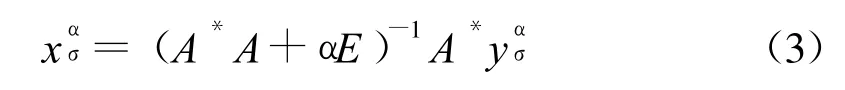
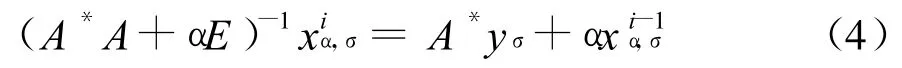
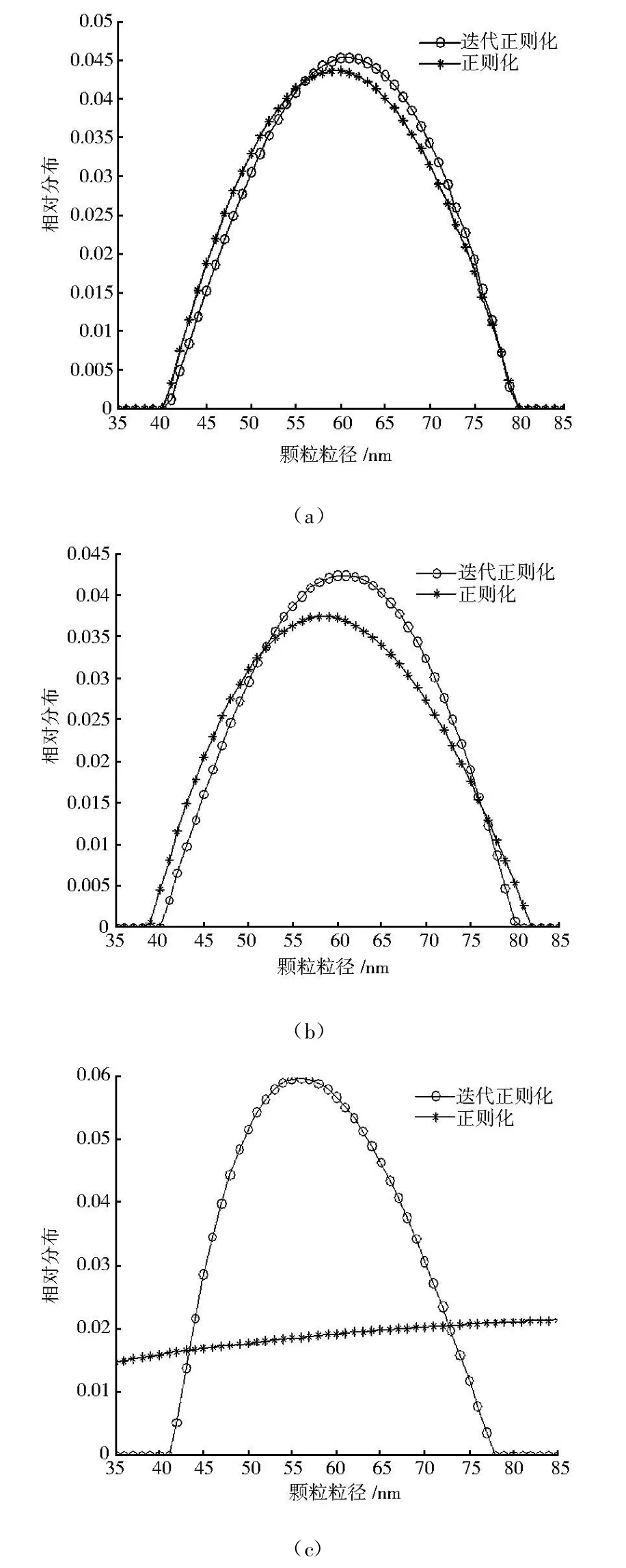
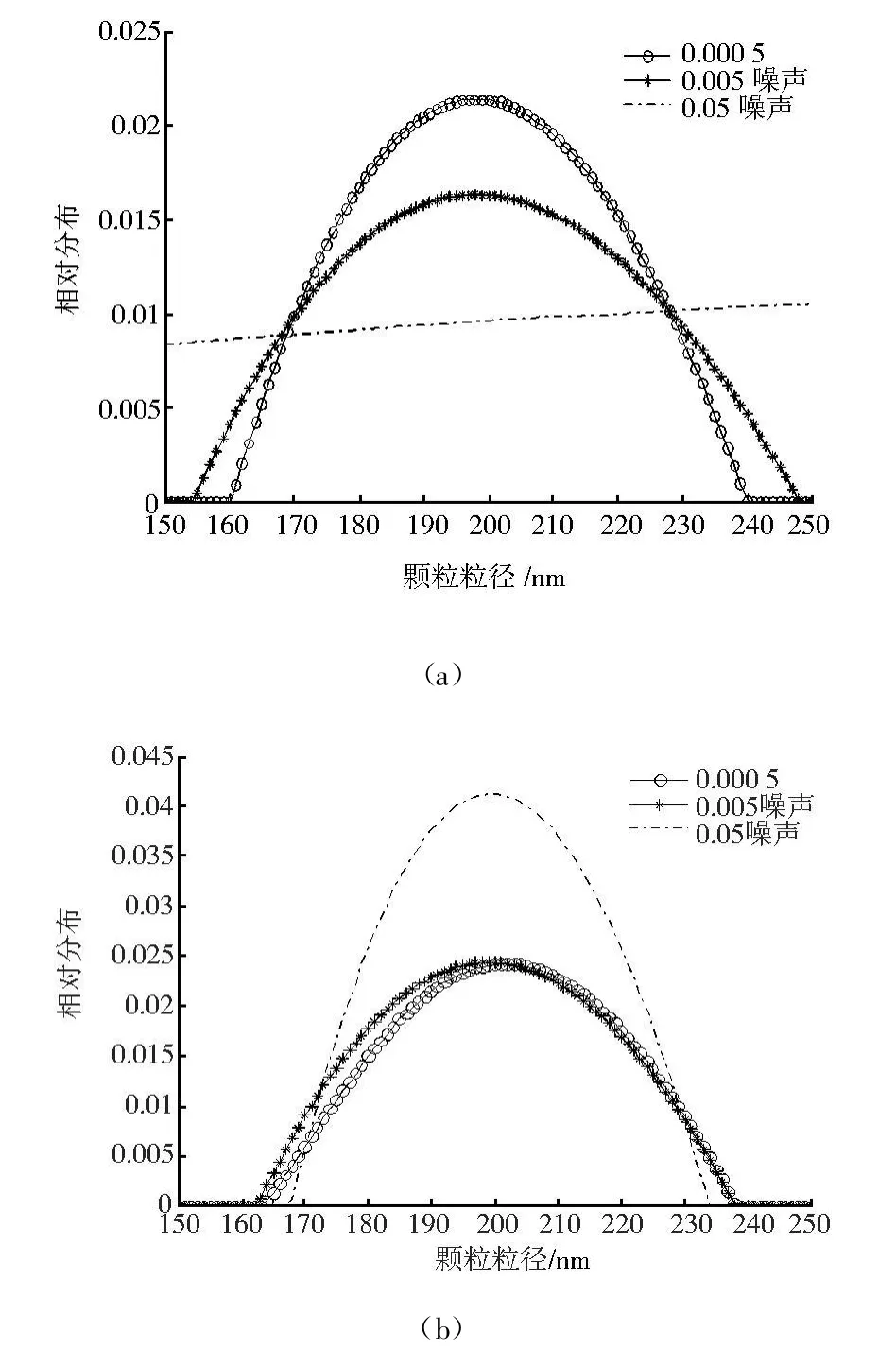
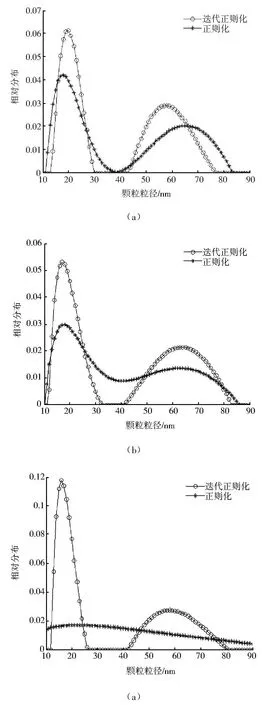
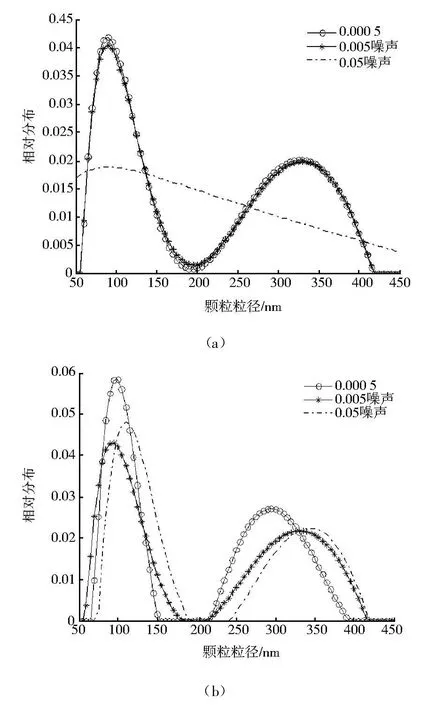
文献[11] 证明了在0 正则化方法的一个关键问题就是正则参数的选取.正则参数的好坏直接影响到解的好坏,甚至会产生无解或多解.正则参数的选取一般有先验和后验策略,CONT IN算法是采用的先验策略.后验策略中广泛采用的原则是Morozov偏差原理 式中δ为误差水平. 为了进一步提高精度,本文采用改进的Morozov偏差原理 正则参数的具体求解见文献[11] . 求出正则参数代入(4)就可以求出粒径分布. 对单峰和双峰分布颗粒的模拟信号进行反演,设模拟信号采用的测量参数为: 入射光在真空中的波长632.8nm,分散介质(水)折射率1.331,黏度系数0.89×10-3N◦S◦K-1,样品溶液温度25℃,波尔兹曼常数KB=1.380 7×10-23J◦K-1,取散射角90°.所加噪声均为白噪声.正则参数初始值=0.03,控制精度ce=10-10,正则化的最大迭代次数kmax=500.迭代正则化最大迭代次数=5,迭代的初始值=0. 在无噪声的情况下,正则化和迭代正则化的收敛阶基本相同,因此,反演的结果相差很小.对于单峰分布的颗粒,正则化和迭代正则化方法都能比较准确的反演,在此不做讨论.本文主要是针对噪声水平为0.000 5,0.005,0.05时,峰值位置为60nm及峰值位置为200nm的单峰分布颗粒的相关函数进行反演,并对反演结果进行了比较分析. 首先对峰值位置为60nm单峰分布颗粒的相关函数在上述噪声水平下进行了反演,反演区间为[35,85] ,反演结果如图1所示. 从图1和表1可以看出,噪声越大,迭代正则化的反演优势越明显.当噪声水平为0.000 5、0.005时,两种方法都能够在给定的反演区间内反演出粒径分布,迭代正则化在峰值位置、峰值高度、分布宽度方面比正则化误差小.当噪声为0.05时,在给定区间内正则化已不能反演出粒径分布,迭代正则化仍能够反演出颗粒粒径. 表1 在噪声情况下,用正则化和迭代正则化方法对60nm颗粒反演得到的峰值 图1 在噪声情况下,用正则化和迭代正则化方法对60nm颗粒反演所得的颗粒粒径分布 在0.000 5、0.005、0.05噪声水平下,对200nm单峰颗粒在区间[150,250] 进行反演,结果如图2所示. 图2 在噪声情况下,用正则化和迭代正则化方法对200nm颗粒反演所得的颗粒粒径分布 图2(a)为正则化方法在三种噪声下对200nm颗粒的反演,图2(b)为迭代正则化方法在三种噪声下对200nm颗粒的反演.由图2可知,在有噪声的情况下,迭代正则化与正则化均随着噪声的不断增大,峰值位置误差逐渐变大,这说明噪声影响了反演精度.当噪声增大时,迭代正则化反演结果的误差变化比正则化小.当噪声为0.05时迭代正则化仍能较准确的反演出粒径分布,而当噪声为0.05时正则化方法已不能反演出颗粒粒径.在同等噪声水平下,迭代正则化反演误差比正则化小. 图3 在噪声情况下,用正则化和迭代正则化方法对20、60nm颗粒反演所得的颗粒粒径分布 多峰分布的反演是动态光散射反演的一个难点,本文以双峰分布颗粒的反演为例,研究迭代正则化对多峰分布的反演.与单峰分布一样,在无噪声的情况下,迭代正则化和正则化方法对双峰分布都能反演出,两者的差别细微,本文就不再详细说明.研究重点为迭代正则化方法和正则化方法在噪声条件下的反演.本文分别在噪声为0.000 5、0.005、0.05的水平下对20、60nm,100、300nm颗粒双峰分布的相关函数进行反演,并对反演结果进行了比较分析. 由图3可以看出,对于20、60nm颗粒,由图3(a)可知噪声为0.000 5时迭代正则化和正则化都能较好的反演出,但迭代正则化在峰值位置、分布宽度、峰值高度更为准确;由图3(b)可知当噪声为0.005时正则化方法能够反演出第一个峰,对于第二个峰就不能很好的反演,而迭代正则化方法对于两个峰都能反演出,并且每个峰值位置的误差均小于5%;由图3(c)可知当噪声为0.05,正则化方法已不能对双峰分布颗粒进行反演,峰值不明显,但迭代正则化方法仍能反演出双峰分布,峰值位置明显,且第一个峰值和第二个峰值位置误差都不大于10%. 图4 在噪声情况下,用正则化和迭代正则化方法对100、300nm颗粒反演所得的颗粒粒径分布 在不同的噪声水平下,采用正则化、迭代正则化方法对100、300nm颗粒的双峰分布进行反演.结果如图4所示,可以看出,正则化方法随着噪声的不断增大,反演误差很大,峰值高度变化也较明显,当噪声水平为0.05时正则化方法已不能反演出颗粒分布,而迭代正则化方法仍能够较好的反演;在同等噪声水平下,迭代正则化反演的颗粒粒径的峰值高度也明显高于正则化,误差水平也小于正则化反演的误差. 采用改进的迭代正则化方法对动态光散射相关函数进行反演,是把前一次反演结果进行回代的一个反复迭代,逐渐逼近真实值的过程,因此得到比正则化方法更高的收敛阶,提高了反演精度.通过对不同的单峰和双峰分布颗粒的反演可以看出,对于单峰分布颗粒,迭代正则化方法能够很准确的反演出.对于双峰分布颗粒,迭代正则化方法的反演优势与正则化方法相比很明显,正则化方法在噪声大于0.005时基本上不能反演出双峰颗粒,迭代正则化方法在噪声为0.05时仍能够很好的反演出双峰分布,且两个峰值位置误差都不大于10%.因此,迭代正则化方法具有较强的抗噪能力. [1] PECORA R.Dynamic Light Scattering.Application of Photon Correlation Spectroscopy[M] .New York:Plenum Press,1985. [2] 王乃宁.颗粒粒径的光学测量技术及应用[M] .北京:原子能出版社,2000. [3] 喻雷寿,杨冠玲,何振江,等.颗粒粒径测量中约束正则CON TIN算法分析[J] .激光生物学报,2007,16(1):74-78. [4] 喻雷寿,杨冠玲,何振江,等.用于动态光散射颗粒测量的迭代CONTIN算法[J] .光电工程,2006,33(8):64-69. [5] 孔明,赵军,李春燕.自动基线拟合累积量算法纳米颗粒反演[J] .光电工程,2009,36(9):52-55. [6] 韩秋燕,申晋,宋景玲,等.PCS颗粒测量技术中的累积分析方法研究[J] .光子学报,2008,37(12):2 525-2 528 [7] 韩秋燕,申晋,孙贤明,等.基于Tikhonov正则参数后验选择策略的PCS颗粒粒度反演方法[J] .光子学报,2009,38(11):2 917-2 926. [8] 肖庭延,于慎根,王彦飞.反问题的数值解法[M] .北京:科学出版社,2003. [9] Fakeev A G.A class of Iterative Processes for Solving Degenerate Sy stems of Linear Algebraic Equations[J] ,USSR.Comp.Math.Math.phys.1981,21(3):15-22. [10] 金其年,侯宗义.关于迭代Tikhonov正则化的最优正则参数选取[J] .高校应用数学学报.1996,11(3):321-328. [11] 傅初黎,李洪芳,熊向团.不适定问题的迭代Tikhonov正则化方法[J] .计算数学.2006,28(3):237-246.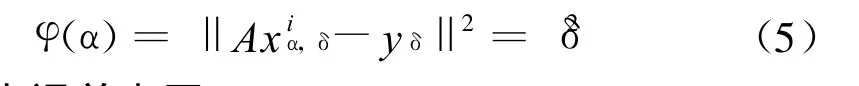
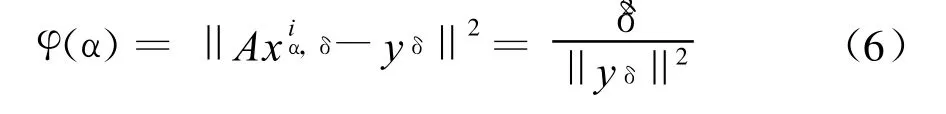
3 颗粒散射光模拟信号的反演与分析
3.1 单峰分布颗粒的反演

3.2 双峰分布颗粒的反演
4 结束语
