基于VaR约束的均值-绝对偏差投资组合优化模型及实证研究

武敏婷，孙 滢，高岳林

（北方民族大学 信息与系统科学研究所，银川 750021）

近年来,随着人工智能技术的发展,把智能优化方法应用于投资组合问题已成为更广阔的研究领域。刘侠,初红霞等用粒子群算法解决证券投资组合问题。本文引入约束机制,提出带有约束的多目标决策模型,并用带有罚函数处理机制的粒子群算法求解证券组合模型最优解问题。

1 基于VaR约束的均值-绝对偏差(VaR-MAD)证券组合优化模型

设证券市场有n种证券,第i种证券的收益率为ri,证券组合的收益率为r=(r1,r2,…，rn)T,证券公司投资于每种证券的金额是任意的,又设在每种收益率水平上的投资者足够多,证券公司投放于每种证券的权重为证券组合的权重向量为x=(x1,x2,…，xn)T,记第i种证券与第j种证券的协方差为σij,证券组合的标准差和回报率分别为σp和rp,E(rp)表示证券组合的期望收益率。

定义1:

称为VaR约束,其中,c为常数。

式(1)表示证券组合收益率rp超过-VaR的概率不低于c,就证券组合而言,当n充分大时,由中心极限定理可认为其组合收益率近似地服从正态分布。因此,为讨论方便，设证券组合的收益率服从正态分布。根据中心极限定理，在正态分布下，证券公司风险承受能力的VaR约束可以转化为Φ-1(c)σp-VaR≤r0，其中Φ(·)为标准正态分布函数，r0为给定的一个常数。

定义2:

称为绝对偏差，其中T为历史数据的个数。

投资者往往在追求高收益的同时要求承受最低的风险，因此构成了该决策的多目标问题。在投资者追求低风险和高收益的前提下，可以得到证券组合投资的多目标规划模型如下:

因此，基于VaR约束的多目标均值-绝对偏差模型为:

式中，r=(r1,r2,…，rn)T为证券组合中n种证券的期望收益率，x=(x1,x2,…，xn)T为投资权重，B=(σij)n×n是 n 种证券的协方差矩阵。

为求解方便，我们把多目标转化为单目标，形式如下:

其中，λ，r0均为常数。λ可以反映投资者的风险偏好，λ越大，投资者越重视收益，属于激进派;反之，投资者越重视风险，属于保守派。

2 模型的求解

2.1 粒子群算法

粒子群优化算法是从鸟类飞行得到启发而提出的优化算法，它将每个优化问题的解看作搜索空间中的一只鸟，在搜索空间中以一定的速度飞行，这个速度根据它本身的飞行经验和同伴的飞行经验来动态调整，第i个粒子在n维空间里的位置表示为矢量 X=(x1，x2，…，xn)，飞行速度表示为矢量V=(v1，v2，…，vn)。每个粒子都有一个适应值，自己到目前为止发现的最好位置(psb)，现在的位置Xip以及到目前为止整个群体的最好位置pgb。

PSO也是基于迭代的优化工具。对于第k次迭代，每个粒子是按照下列公式进行变化：

rand()是[0,1]之间的随机数，c1和 c2被称作学习因子，ω是惯性权重加权系数，如果ω较大，则算法的全局搜索能力较强；反之，局部搜索能力较强。

本文通过采用群体适应度方差和平均粒距判断算法[9]是否出现早熟现象，如果算法陷入局部收敛，则通过对适应值较差的部分粒子进行变异，从而跳出局部最优解进行全局搜索。

2.2 模型的求解

对于多目标问题来说,本中用加权法将多目标转化为单目标,结合罚函数处理机制又将其转化为无约束问题,利用自适应粒子群算法进行求解,运用混合罚函数的自适应粒子群算法,具体的混合算法流程如下:

Step1:随机初始化粒子群:群体规模为n,包括粒子的随机位置与速度，并进行标准化处理，使它满足约束条件

Step2:将粒子的psb设置为当前位置，pgb设置为初始种群中最佳粒子的位置；

Step3:计算粒子的适应值:适应度模型(4)的目标函数计算,其中Q为一充分大的正数，

用式(7)来评价每个粒子的适应度并进行排序,判断算法收敛准则是否满足,如果满足,转向Step9;否则,执行Step4;

Step4:对于粒子群中的所有粒子,执行如下操作:

(1)根据式(5)、(6)更新粒子的位置与速度；

(2)如果粒子适应度优于psb的适应度,psb设置为新位置；

表1 六种证券在八年的年收益率数据

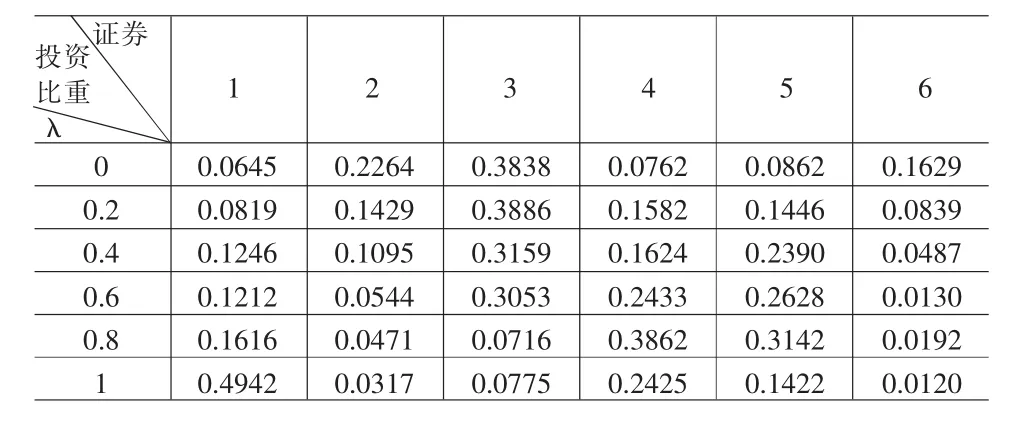
表2 当固定λ变化时VaR-MAD模型的证券投资比重

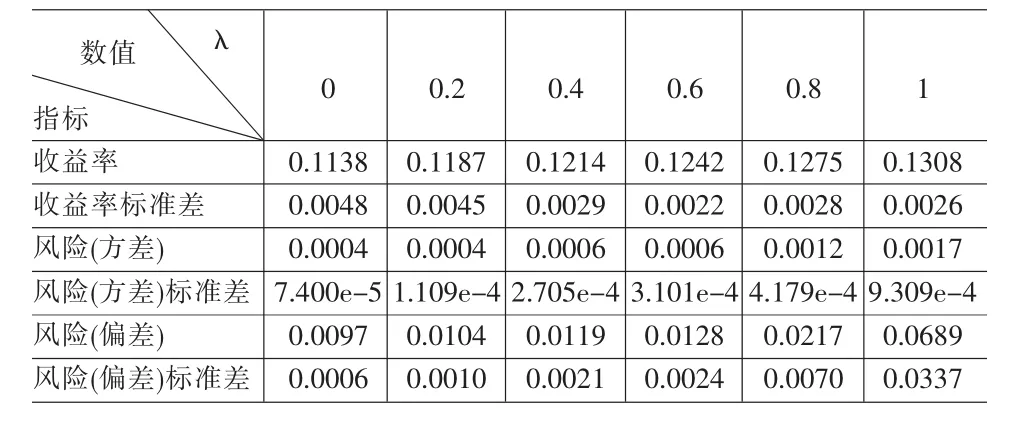
表3 当固定λ变化时VaR-MAD模型的六种指标

表4 当固定r0变化时VaR-MAD模型证券投资比重

表5 当固定r0变化时VaR-MAD模型的六种指标

表6 当λ=0.6时MAD模型和VaR-MAD模型的投资比重

表7 当 λ=0.6时MAD模型和VaR-MAD模型的不同指标

(3)如果粒子适应度优于pgb的适应度,pgb设置为新位置；

Step5:计算群体适应度方差和平均粒距，并计算f(pgb)；

Step8:判断算法收敛准则是否满足，如果满足,执行Step9,否则,转向 Step4；

Step9:输出pgb,算法运行结束。

3 实证分析

本文借鉴文献[11]中的数据,如表1所示。假设给定的VaR=5%，c=95%，即Φ-1(c)=1.65，即该证券公司的风险承受能力为:在置信度为95%的情况下，最大损失不低于5%。

设六种不同证券的投资权重x=(x1,x2,x3,x4,x5,x6)T，我们将上面的数据带入到本文中的模型(5)中进行求解，在MATLAB中用智能优化算法-自适应粒子群算法来实现,取学习因子c1=2,c2=2组合权重因子为μ=0.5，最大和最小惯性权重分别为ωend=0.9，ωini=0.4种群规模N=30，最大迭代次数Tmax=100。惩罚因子Q=1000,我们分情况讨论，当 r0为一定值 0.2时，取λ=0、0.1,0.4,0.6,0.8;1当λ为一定值0.6时，取r0=0.2,0.4,0.6,0.8,十种情况分别运行20次,并对结果进行分析,运行结果如表2-表5。当λ取0.6时,又用粒子群算法求解MAD模型,运行结果与VaR-MAD模型比较(表6和表7)。

我们从表2～5四个表可以看出:当VaR约束阈值r0为一定值时，(1)随着λ的增大，证券1、3和4的比重增大，而其余三种证券的比重减小;(2)λ反映投资者的风险偏好程度，随着其值的增大，收益增大，风险增大，而收益的波动程度相对减小,风险的波动程度增大。当λ为一定值时，(3)随着VaR约束阈值的增大,证券1、2和5的比重增大,而其余三种证券的比重减小;(4)VaR约束对收益的影响不是很大,主要作用是对风险的控制,在收益一定的情况下，使得风险达到最小。以上结论比较符合客观实际。

由表6和表7，我们可以看出,本文中建立的VaR-MAD模型与MAD模型相比，前者使投资者在一定收益的水平下,风险得到了有效控制。

当r0=0.20时，我们得到VaR-MAD模型的有效前沿（见图 1）：

4 结束语

本文通过增加约束对证券组合的收益和风险进行控制和优化，该方法既能控制证券公司的潜在风险损失，又能兼顾证券公司的长远发展，提高证券公司投资决策的科学性。在实际操作过程中，决策者可根据对客观实际情况的把握,证券公司的资本充足情况以及有关证券公司投资证券的法律、法规等，采用定性和定量相结合的分析方法,对组合证券的收益、风险和投资权重进行优化选择，使决策更符合客观现实。

[1]Markowitz H.Portfolio Selection[J].The Journal of Finance,1952,7(1).

[2]Jorion P.Value-at-Risk:The New Benchmark for Controlling Market Risk[M].New York：The Mc Graw-hill Companies,Inc,1997.

[3]Dowd K.Beyond Value-at-risk[M].New York:John Wiley&Sons,Inc,1998.

[4]Best P.Implementing Value-at-risk[M].New York:John Wiley&Sons,Inc,1998.

[5]迟国泰,王际科,齐菲.基于风险度量和风险控制的贷款组合优化决策模型[J].预测,2009,28,(2).

[6]徐永春,高岳林,甘斌.一致性风险测度下的和对比研究[J].统计与决策,2009,(6).

[7]徐永春,高岳林.金融风险管理的方法及实证分析[J].求索,2009(2).

[8]刘侠,初红霞,王科俊.基于粒子群算法的证券组合投资模型的研究[J].商业研究,2006,(16).

[9]安晓会,高岳林.混合变异算子的自适应粒子群优化算法[J].计算机应用,2008,28(3).

[10]解可新,韩立兴,林友联.最优化方法[M].天津大学出版社,2002.

[11]刘善存,汪寿阳,邱菀华.一个证券组合投资分析的对策论方法[J].系统工程理论与实践,2001,（5）.