模糊综合评判决策模型的缺陷与消除
2010-07-23张世强吕杰能
张世强,吕杰能,蒋 峥,张 雷
(重庆医科大学 数学教研室,重庆 400016)
基于模糊综合评判的决策模型几乎在所有的模糊数学教科书及关于模糊数学应用的专著中都会提到,其基本模型是许多涉及到模糊综合决策的应用性论文常用的模型[1],[2]。《统计与决策》2005年11期刊载的“基于模糊综合评判下的决策模型”再次介绍了该基本模型,并给出了“成功决策”的实例[3]。针对该实例,《统计与决策》2006年12期刊载的“一种不合理的模糊综合评判下的决策模型”则指出该实例对应的决策会出现自相矛盾的结果[4]。即基于模糊综合评判的基本决策模型是有缺陷的,其根源来源于基本模型在进行模糊综合决策时使用的算子。本文将给出消除该缺陷的方法。
1 基本决策模型
设评价对象具有m个属性,构成的因素集合记为U={u1,u2,…,um};对于各个因素,可能取得 n 个评价,构成的评价集合记为 V={v1,v2,…,vn}。
对于评价对象的每一个属性或因素ui都有一个模糊决策集合 Ri={ri1,ri2,…,rin}∈F(U×V),m 个属性或因素共有 m 个模糊决策集合,可以用模糊矩阵表示为:

称R为因素决策矩阵。
如果评价对象的m个因素的权重分配集合为A={a1,a2,…,am},则模糊决策矩阵B可由下式求出:

其中,算符“◦”表示模糊合成运算。
在广义模糊运算下,模糊决策矩阵B的第j个元素的计算式为:

其中“▽”表示广义模糊“与”运算;“△”表示广义模糊“或 ”运算。按此运算获得的模糊决策矩阵B简记为模糊决策模型 M(▽,△)。
模糊数学教科书及关于模糊数学应用的专著中给出的基于模糊综合评判的基本决策模型一般有如下四类。
基本决策模型一:M(∧,∨)。
用取小运算符“∧”代替广义模糊算子“▽”;用取大运算符“∨”代替广义模糊算子“△”。此时,模糊决策矩阵B的第j个元素的计算式为:

基本决策模型二:M(·,∨)。
用普通乘法运算符“·”代替广义模糊算子“▽”;用取大运算符“∨”代替广义模糊算子“△”。此时,模糊决策矩阵B的第j个元素的计算式为:

基本决策模型三:M(·,⊕)。
用普通乘法运算符“·”代替广义模糊算子“▽”;用运算符“⊕”代替广义模糊算子“△”,其中运算符“⊕”定义为:

此时,模糊决策矩阵B的第j个元素的计算式为:

基本决策模型四:M(·,+)。
用普通乘法运算符“·”代替广义模糊算子“▽”;用普通加法运算符“+”代替广义模糊算子“△”。此时,模糊决策矩阵B的第j个元素的计算式为:
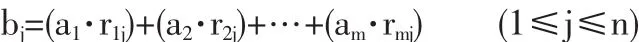
另外还有一些类似的基本决策模型,不再赘述。之所以会出现如此多的所谓的“基本决策模型”,其原因是当初采用“基本决策模型一”时,出现了“决策失效”的情况。为了解决该问题,于是就派生出了这些“基本决策模型”。不幸的是,这些“基本决策模型”总会出现这样或那样的问题。更不幸的是,创造这些“基本决策模型”的人没有从根本上去找发生问题的原因,而始终在做一些查漏补缺的工作。
文献[2]发现这些“基本决策模型”出现问题时,给出的分析是:
模型一为“主因素决定型”。但对于有的问题,可能会丢失很多的信息,因而得到的结果有些粗糙。解决的方法是不将评价对象的m个因素的权重分配集合A={a1,a2,…,am}归一化,或者采用模型三或模型四。
模型二为“主因素突出型”。评价对象的m个因素的权重分配集合 A={a1,a2,…,am}不必归一化。

表1

表2
模型三和模型四为“加权平均型”。评价对象的m个因素的权重分配集合 A={a1,a2,…,am}应该归一化。
为了说明这些“基本决策模型”及其给出的分析有效,文献[2]给出了如下的关于教学过程的综合评价实例分析。
设U={清楚易懂,熟悉教材,生动有趣,板书工整}。评判分为四级:V={优,良,中,差}。用打分的方法对某教师的一堂课给出各因素的评价。评价结果见表1。
对于权重分配集合A,设专家对U中各因素的重要程度给出的评价为:
A={0.9,0.4,0.4,0.2}
则模糊决策矩阵B的计算式:

按照模型一计算出的模糊决策矩阵B=[0.4,0.45,0.4,0.1];
按照模型二计算出的模糊决策矩阵B=[0.36,0.41,0.22,0.04];
按照模型三,先把权重分配集合A归一化,计算得A={0.5,0.2,0.2,0.1}; 然后计算出的模糊决策矩阵 B=[0.34,0.38,0.25,0.03];
按照模型四,先把权重分配集合A归一化,计算得A={0.5,0.2,0.2,0.1}; 然后计算 出的模糊决 策矩阵 B=[0.34,0.38,0.25,0.03]。
使用上述四个评判决策模型,均得出某教师这堂课为“良”的结论。至于为什么模糊决策模型三和四的模糊决策矩阵完全相同,文献[2]及几乎所有的模糊数学教科书和关于模糊数学应用的专著没有引起注意和作出解释。本文后面讨论部分会给出详细的解释。
2 基本决策模型引发的争论
针对文献[2]给出的四个基本决策模型和实例,文献[4]指出:基本决策模型M(∧,∨)是不合理的。因为该模型的最终决策结果取决于某个(或某几个)数字。例如上例中,由于因素“清楚易懂”的权重为0.9,理论上可能出现某教师的一堂课的评价结果如表2。
按照模型一计算出的模糊决策矩阵B=[0.45,0.4,0.2,0.4];
按照模型二计算出的模糊决策矩阵 B=[0.405,0.18,0.09,0.225]。
这两个评判决策模型,均得出某教师这堂课为“优”的结论。
按照模型三,先把权重分配集合A归一化,计算得A={0.5,0.2,0.2,0.1}; 然后计算出的模糊决策矩阵B=[0.3,0.225,0.12,0.325];

表3

表4
按照模型四,先把权重分配集合A归一化,计算得A={0.5,0.2,0.2,0.1}; 然后计算出的模糊决策矩阵B=[0.3,0.225,0.12,0.325]。
这两个评判决策模型,却得出某教师这堂课为“差”的结论。
文献[4]指出:这完全相反的评判结果令人无法接受。其原因是基本决策模型M(∧,∨)和M(·,∨)中的算子∧和∨的不合理性。
《统计与决策》2005年11期刊载的“基于模糊综合评判下的决策模型”再次介绍了该基本模型,并给出了“成功决策”的实例[3]。
设因素集合U={教学态度,教学内容,教学方法,教学手段,教学效果}={u1,u2,u3,u4}。 评语集合分为四级:V={优秀,A类,B 类,C 类}={v1,v2,v3,v4}。
学校规定,分数在95以上者为优秀;分数在90~94之间者为A类;分数在65~89之间者为B类;分数在64分以下者为C类。假定某班共有学生60人,用打分的方法表示各自对评判教师的评价。甲教师的评价结果见表3。
对于权重分配集合A,设专家对U中各因素的重要程度给出的评价为:
A={0.30,0.20,0.20,0.10,0.20}
则模糊决策矩阵B的计算式B=A◦R。
文献[3]按照模型一计算出的模糊决策矩阵B=[0.30,0.25,0.20,0.10]。B(x1)最大,文献[3]据此得出学生对甲教师的教学质量评价为“优秀”的结论。
针对该实例,《统计与决策》2006年12期刊载的 “一种不合理的模糊综合评判下的决策模型”则指出该实例对应的决策会出现不合理,甚至荒唐的结果[4]。
文献[4]给出的反例1如下:理论上可能存在某教师(乙教师)只要在教学态度上得到学生的好评,其他教学环节均很差,仍然可能被“综合”评判为“优秀”。假设因素“教学效果”的评价打分是以期末学生的考试成绩来确定,学生考试成绩为多少分就认为该生给教师打了多少分。于是完全有可能出现乙教师的考评,在前四个因素的得分情况与上述例中的甲教师的打分情况完全一样,唯独教学效果的得分有差别。即:甲教师在因素“教学效果”上的得分为{0.30,0.50,0.10,0.10};乙教师在因素“教学效果”上的得分为{0.10,0.10,0.10,0.70},显然二者有极大的差异。
但按照模型一计算出来的模糊决策矩阵,均得出D(x1)最大,得出了乙教师与甲教师一样,教学质量评价均为“优秀”。这就是说,甲教师所教的学生的期末考试成绩中有80%的学生的成绩在90分以上,而乙教师所教的学生的期末考试成绩中有70%的学生的成绩在64分以下,而两位教师的教学质量的综合评价等级却均为“优秀”。评价结果的不合理性是显然的。
文献[4]给出的反例2如下:理论上可能存在更为极端的情况,某教师(丙教师)的教学质量得分情况如表4。
显然该教师除了在教学态度上得到一半学生的认可外,其他教学环节均很差。
但按照模型一计算出来的模糊决策矩阵,均得出D(x1)最大,得出了丙教师与甲教师一样,教学质量评价均为“优秀”。评价结果显然荒唐。
争论的根源自然来自基本决策模型中广泛使用的取小取大算法。该算法得到的结果只取决于某一个或几个因素,其它因素根本不起作用。显然基本决策模型中的取小取大算法遗漏了很多信息,这就是基本决策模型隐藏的缺陷。而几乎所有的模糊数学教科书及关于模糊数学应用的专著又都将取小取大算法运用于模糊综合评判,其结果就导致了绝大多数涉及到模糊综合评判的应用性论文会通过所谓的“改进方法”,得出有利于作者意图的“评判结果”。这样的模糊综合评判结果理论上很难令人信服,是否具有实际应用价值亦令人生疑。
3 消除基本决策模型隐藏的缺陷的方法
基本决策模型隐藏有缺陷的原因是使用了只取决于某一个或几个因素,其它因素根本不起作用的取小取大算子。文献[5]介绍的 Einstain 算子可以克服取小取大算子遗漏信息的缺陷。所以在基本决策模型中,用Einstain算子取代取小取大算子可以消除基本决策模型隐藏的缺陷。Ein⁃stain 算子的定义为:

对于上面文献[2]的示例和文献[4]针对文献[2]的结论给出的反例,对于权重分配集合 A={0.9,0.4,0.4,0.2},采用 E⁃instain 算子算出关于表1相关的模糊综合向量为:B={0.5126,0.5533,0.3665,0.0376},B(x2)最大,据此可得出学生对该教师的教学质量评价为“良”的结论;采用Einstain算子算出关于表2相关的模糊综合向量为:B=[0.4641,0.3686,0.1712,0.4644],B(x4)最大,据此可得出学生对该教师的教学质量评价为“差”的结论。这与文献[4]的分析结果是相吻合的。
而对于权重分配集合A={0.9,0.4,0.4,0.2}的归一化矩阵A={0.5,0.2,0.2,0.1},采用 Einstain 算子算出关于表1相关的模糊综合向量为:B={0.2480,0.2716,0.1722,0.0172},B(x2)最大,据此可得出学生对该教师的教学质量评价为“良”的结论;采用 Einstain 算子算出关于表2相关的模糊综合向量为: B=[0.2192,0.1702,0.0755,0.2216],B(x4)最大,据此可得出学生对该教师的教学质量评价为“差”的结论。同样与文献[4]的分析结果相吻合。
该例还说明,在基本决策模型中,用Einstain算子取代取小取大算子后,对于权重分配集合A归一化与否,并不影响综合决策的结论。
对于上面文献[3]的示例和文献[4]针对文献[3]的结论给出的反例, 对于权重分配集合 A={0.30,0.20,0.20,0.10,0.20},采用Einstain算子算出关于表3相关的模糊综合向量为:B={0.2802,0.2496,0.0787,0.0472},B(x1)最大,据此可得出学生对甲教师的教学质量评价为“优秀”的结论;采用Einstain算子算出关于表4相关的模糊综合向量为:B=[0.1007,0.0569,0.0787,0.4702],B(x4)最大,据此可得出学生对丙教师的教学质量评价为“C类”的结论。文献[4]中提到的丙教师与甲教师同样“优秀”的荒唐结果不再呈现。
4 讨论
模糊集合理论的基本运算符是取小取大运算符,几乎所有的模糊数学教科书和模糊数学专著都将取小取大算法应用于基本决策模型。 由于该算法得到的结果确实只取决于某一个或几个因素,其它因素根本不起作用,遗漏了很多信息。其结果就导致了绝大多数涉及到模糊综合评判的应用性论文会通过选择基本决策模型得出有利于作者意图的“决策结果”。这样的模糊综合决策结果理论上很难令人信服,是否具有实际应用价值(见文献[4]中的反例)亦令人生疑。另外,虽然通过选择基本决策模型,可以得到模糊综合决策结果,但却导致模糊综合决策的标准不统一,使文献之间的结论不具备可比性。
还有不少文献用线性代数中的乘和加算子(·,+)进行模糊综合决策。但这些文献都没有注意到其中的“+”算子并不满足模糊数学中的三角算子的两极律,即加算子“+”不是余三角范算子,运算于模糊幂集是否会引发其它问题是值得商榷的[5]。为什么这些文献用线性代数中的乘和加算子(·,+)也作出了“正确”的评判结果呢?这是因为在被评判的实例中,恰好不会出现a+b>1的情况,此时线性代数中的乘和加算子(·,+)恰好等价于三角算子组合,即是用来评判的(其中a⊕b=min{a+b,1}),对于使用者来说并未意识到这一点。
最后需指出的是,取小取大算子是线性算子,从上面实例分析可知,它是一个具有可变漏洞的算子,这是产生争论的根源。Einstain算子是非线性算子[5],故能够充分利用原始数据提供的全部信息。
[1]李洪兴,王培庄.模糊数学[M].北京:国防工业出版社,1994.
[2]曹炳元.应用模糊数学与系统[M].北京:科学出版社,2005.
[3]谢小良.基于模糊综合评判下的决策模型[J].统计与决策,2005,(11).
[4]周学松,苏为华.一种不合理的模糊综合评判下的决策模型[J].统计与决策,2006,(12).
[5]Zhang Shi-Qiang.Method of Checking up Concealed Faults on the Fuzzy Controller[C].The Proceedings of the China Associa⁃tion for Science and Technology,2008,1(4).
