不同产量分布下湖北省县级水稻产量保险的纯费率厘定

刘锐金，凌远云，王成丽

（1.中国热带农业科学院橡胶研究所，广东 儋州 571737；2.华中农业大学 经济管理学院，武汉 430070；3.广东省增城市派潭镇政府，广东 增城 511386）

0 引言

农业保险作为农业风险管理的重要手段，越来越受到党中央国务院的重视。从2004年起，连续6年的中央一号文件都强调要开展政策性农业保险，目前已经试点的农作物保险险种覆盖了小麦、玉米、棉花和水稻等。湖北省从2007年开始在黄石、阳新、黄梅、新洲、竹溪、老河口、应城等地开展政策性水稻保险，该保险对由自然灾害和病虫害直接造成的叶片毁坏、茎杆折断、倒伏或死亡且损失程度达到20%以上时进行赔付。每亩水稻的保险金额为200元，按季每亩保费14元，费率为7%。由于水稻保险的保险金额为水稻生长期内所发生的直接物化成本，赔偿触发时，农户得到的只是恢复生产的物化成本补偿，并不能很好地化解农业风险。湖北省现行的水稻保险属于个人保险，存在一定的道德风险；在自愿参保和无补贴的情况下，该保险可能存在逆选择；理赔成本较高，某个农户发生损失时，保险公司需要对该农户进行核损、理赔。根据Roberts(2005)的研究，该保险在经营中存在很多障碍。

农作物区域产量保险是经国外实践检验的一种较好的化解农业风险的保险制度创新。在美国，农作物区域产量保险已经实行多年，也有很多的研究。从保险经营角度来看，区域产量保险可以在很大程度上减少或消除道德风险发生的可能性，可以显著减少逆选择，其次在定损和理赔等方面有便利之处。Skees,Hazell,and Miranda(1999)认为在发展中国家，农作物产量保险可以成为农户分散自然灾害风险的有效工具，其中区域产量保险是一个好的选择。而任何保险合同的基本参数就是费率，有必要对我国农作物区域产量保险纯费率的厘定深入研究，为我国探索农作物区域产量保险提供一些有价值的参考信息。

农作物区域产量保险纯费率的计算依赖于两个关键因素：一个是农作物单位面积产量的分布f(x)；另一个是农作物区域产量保险中相应的保障产量Yc。对于农作物单位面积产量分布f(x)，现有文献中提出了很多统计模型：(1)参数产量模型，Just and Weninger(1999)认为农作物产量趋势服从正态分布，而 Day(1965)、Taylor(1990)、Ramírez(1997)and Ramírez,Misra,and Field(2003)则反对这个观点。Nelson and Preckel(1989)认为农作物产量服从Beta分布；Moss and Shonkwiler(1993)使用逆双曲线正弦变换；Gallagher(1987)则认为是Gamma分布。Sherrick等(2004)则是使用正态分布、对数正态分布、Beta分布、Weibull分布、Logistic分布分别拟合个体产量数据，并对结果进行了比较分析。(2)半参数模型，Ker and Cobbe(2003)。(3)非参数模型，Goodwin and Ker(1998)、Turvey and Zhao(1999)。(4)实证贝叶斯非参数模型，Ker and Goodwin(2000)。很多学者使用不同分布来拟合农作物单产，对于湖北省水稻县级单产使用哪种分布来拟合更合适呢？不同的分布假设下所厘定的湖北省县级水稻产量保险的纯费率是否有差异呢？本文利用1991～2007年湖北省县级水稻单产的数据来厘定县级水稻产量保险的费率，试图回答这些问题。

1 数据来源与预处理

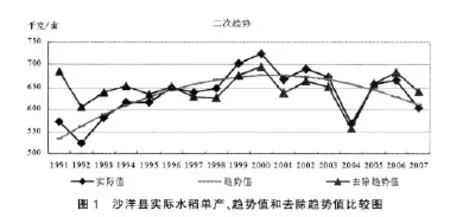
本文使用1991～2007年来自《湖北农村统计年鉴》的县级水稻产量的数据，共有82个县级单位①这17年期间，有一些县市合并或分离，这里描述的年份是根据《湖北农村统计年鉴》的统计，可能与实际撤并的年份有出入，这里只列出有影响的撤并。1991～1995年江夏区原名为武昌县，1991～1993年蔡甸区原名为汉阳县，1994～1995年均为武汉市郊区；1991～1998年沙洋是荆门的一个区；1991～1996年团风县属于黄冈地区的黄州市；1991～1995年，夷陵区原名为宜昌县，宜都市原名为枝城市；1991～1993年，孝昌县是孝感地区的孝感市；1991～1993年，荆州市辖区为沙市市；1995～1998年，江陵县并入荆州市辖区。。2007年全省水稻总播种面积为2177.68公顷，总产量为15248500吨。监利县的总产量最高，而单产最高的是钟祥市。

首先要进行去除趋势处理。去除趋势一般有确定性确实模型和随机趋势模型，一般文献使用确定性趋势模型，本文亦采用此模型。在一次时间趋势下进行回归，在0.1显著性水平下，只有45个县市通过检验。而在二次趋势下，0.05显著性水平就有52个县市通过检验，在0.1下则有60个。因此本文采用二次趋势模型来去除趋势。去除趋势公式：

使用去除趋势的水稻单产，计算各县市水稻单产的均值、标准差、峰度和偏度。所有县市所有年份的平均值为483.51千克/亩，最大的是钟祥市856.86千克/亩，最小的是通山县315.86千克/亩；标准差的平均值为35.616，最大的是襄樊市辖区132.06，最小的是松滋市为8.11；最大峰度为6.98，最小为-1.40；最大偏度为 2.29，最小为-2.64，大部分县市的偏度小于0，具有左偏性。样本数据的偏度和峰度分布情况见图2。

2 各种产量分布假设

选择参数分布一般会考虑到样本数据统计量(例如峰度、偏度)、作物产量的固有特征(例如下界为0)、前人的研究等。图2给出样本数据的峰度-偏度图，可以发现大部分县市的水稻产量是不对称的。根据前人的研究，本文选择Normal、LogN ormal、Logistic、Beta、Weibull分布来拟合各县市的水稻单产。

3 最大似然估计(MLE)及结果

使用极大似然法来估计以上五个分布的参数值。正态分布、对数正态分布、Beta分布④从上述介绍的Beta分布密度函数可知，0＜x＜1。为了使单产数据落入这个区间，参照Zanini etc.(2001)的做法，将各年的水稻单产除以最高产量的1.1倍。、Weibull分布参数的极大似然估计值使用Matlab计算得到，Logistic分布参数的估计值使用R软件得到⑤http://www.wessa.net/rwasp_fitdistrlogistic.wasp提供了使用R软件计算Logistic分布参数的极大似然估计值的对话框和程序。。文中涉及的每个分布都有两个待估计的参数，因此，在用极大似然法估计每个地区的五个分布的参数时，具有相同的自由度。表2给出了部分县市的不同分布的参数估计值，参数本身有很多的含义。

图2是去除趋势产量的偏度与峰度及拟合各分布的偏度与峰度⑥偏度β1=E(X-EX)3/(E(X-EX)2)3/2，峰度β2=E(X-EX)4/(E(X-EX)2)2-3实际计算E(X-EX)3和E(X-EX)4时，采用数值积分的方法实现，Beta分布积分区间为(0,1)，步长为0.000001，其他为[0,1200]，步长为0.001。计算分位数和期望损失也是用这样方法。。偏度小于0的县市有67个，即标准化后的分布比标准正态分布更平坦，且具有左偏性，而峰度大于0的县市有46个，小于0的有36个。正态分布的峰度和偏度都等于0，因为其标准化后的分布就是标准正态分布；Logistic分布具有对称性，因此其偏度为0，但其标准化分布比标准正态分布更陡峭，峰度为1.2；绝大部分县市在对数正态分布下，峰度和偏度都大于0，概率密度函数具有右偏性，即在右边有长“尾巴”，其标准化分布比标准正态分布更陡峭；绝大部分县市在Weibull分布下，偏度小于0，峰度大于0，概率密度函数具有左偏性，其标准化分布比标准正态分布更陡峭；在Beta分布下，偏度大于0，峰度接近于0，概率密度函数具有左偏性，其标准化分布接近标准正态分布。

拟合优度检验，其根本思想是通过比较样本分布曲线和该分布理论分布曲线之间的差距大小，进而判断该分布是否能够对样本观测值进行很好的拟和，常用的拟合优度检验方法有卡方拟合优度检验、Kolmogorov-Smirnov（K-S）检验和Anderson-Darling（AD）检验。 Sherrick etc(2004)总结认为 AD检验更适合测度各分布的拟合优度。

Law and Kelton(2000)给出了AD统计量的定义

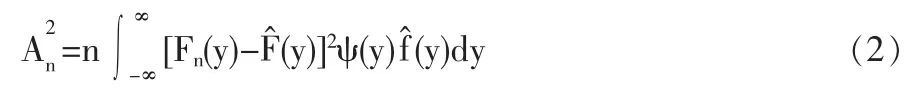
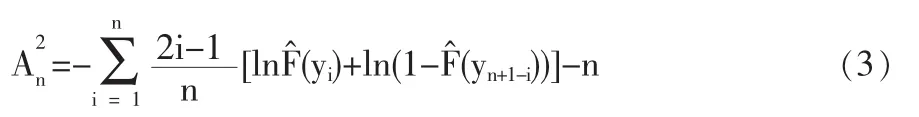
其中yi表示样本数据从小到大排序后处于第i位的样本。

AD统计量实际上测度各样本点在经验分布与拟合分布之间的距离，相比于K-S检验，AD检验赋予样本分布尾部数据更大的权重。我们计算了每个地区的每个分布下的AD统计量，受篇幅的限制，只给出表1作简单描述。在Anderson-Darling检验下，38个县市在Logistic分布假设下拟合得最好，有30个县市在Weibull分布假设下拟合得最好，说明大部分县市在有较高峰度的Logistic和有偏的Weibull分布下拟合得比较好。64个县市在Beta分布下，AD统计量排在第2、3位。60个县市在LogNormal分布下拟合得最差。从总体来看，Logistic分布拟合效果最好。

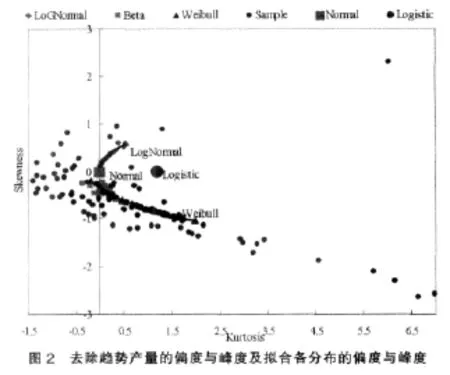
表2给出了沙洋县不同分布在 5%、10%、25%、50%、75%、90%的分位数。沙洋县的水稻单产在Logistic分布下10%分位点是611.39千克/亩，也就是说在该分布假设下，沙洋县的水稻单产小于等于611.39千克/亩的概率为0.1，50%分位数为 648.56千克/亩，1991～2007年该县的平均值为635.00千克/亩。我们对各地区五种分布的六个分位数进行单因素方差分析，发现它们并无显著差异。

4 不同分布下的纯费率比较

农作物区域产量保险中，保险公司给出关键产量 (即100%保障水平下的产量)，农户可以选择不同的保障水平。设关键产量为yk，保障水平为h，则保障产量为Yg=h×yk。又设购买保险合同约定农作物的单位产量价格为Pg，该区域的实际产量为y。如果y≥Yg，则保险公司不对任何投保人赔付，即使投保人的农作物单产低于Yg；如果y＜Yg，则保险公司对所有投保人赔付，单位面积的赔付金额都为(Yg-y)Pg。实际生产历史法(Actual History Production,APH)设置关键产量为历年观测产量的平均值，参照Sherrick etc(2004)的做法，我们选取2001～2007年水稻单产的平均值作为关键产量。设损失变量为L，则L=Pgmax{0,Yg-y}，期望损失为：

前文计算得到了各县市各分布的极大似然估计值，即得到了各县市各分布的概率密度函数f(y)。费率公式：

表3是湖北省县级水稻产量保险在各分布假设的纯费率的总体描述，表4给出各县市最优分布下的纯费率。64个县市在Weibull分布假设下的费率最高，该分布下各县市的平均纯费率4.0767%；15个县市对数正态分布假设下最高，该假设下的平均纯费率3.8855%；Beta分布假设下的平均纯费率3.7000%，处于第3位。这两个分布都属于有偏分布。正态分布下的纯费率处于最低的县市有64个，平均费率最低；比标准正态分布更陡峭且对称的Logistic分布下的平均纯费率约比正态分布假设下高0.4%，处于第4位。由此可以发现，非对称分布下的纯费率要高于对称分布。最优分布下的纯费率与标准差的Pearson相关系数为0.7873，而标准差反映整个经验期的水稻产量波动。这说明纯费率能够在较大程度上反映该地区种植水稻的产量风险。由表3和表4，荆门市辖区的费率明显高于沙洋县、钟祥市和京山县12，荆门市辖区水稻单产的标准差为79.126，而其他3个县分别为32.966、30.68、31.744。

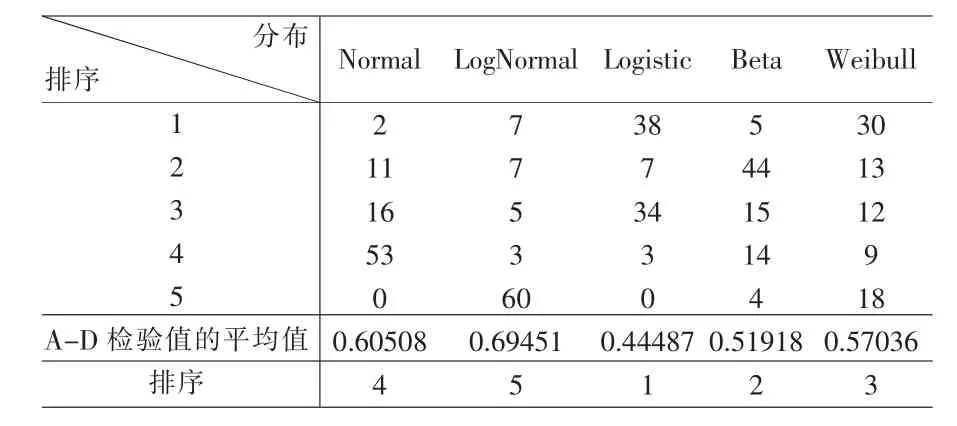
表1 AD检验结果

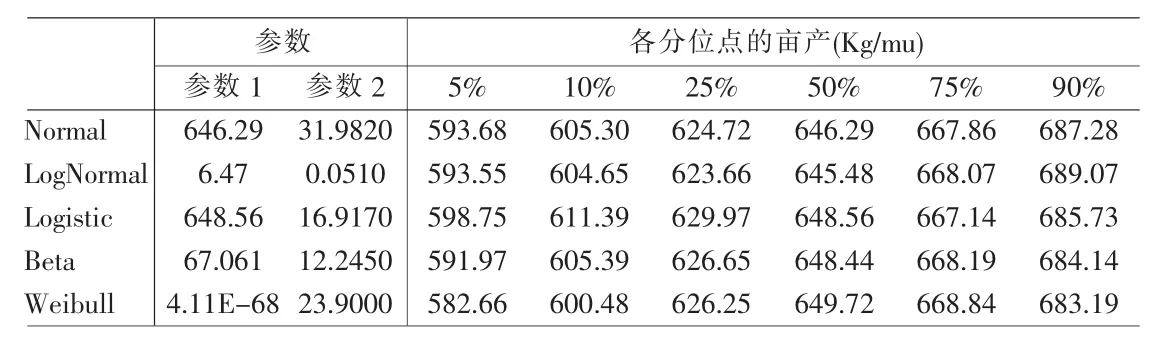
表2 沙洋县各分布的参数估计值和分位数

不同分布假设下所厘定费率的相关系数都大于0.88，说明不同分布假设下所厘定的费率具有很高正相关性，也就是水稻种植风险高的地区在不同分布假设下都有较高的纯费率。但是方差分析表明五种分布假设下的纯费率在1%显著性水平下都有显著的差异，也就是说精确纯费率的厘定依赖于单产分布的正确选择。

5 结论与讨论

本文使用二次确定性趋势模型去除产量的时间趋势，使用极大似然法估计了五种分布的参数。以2001～2007年的平均产量作为关键产量，以拟合的分布作为产量分布，厘定了湖北省县级水稻产量保险100%保障水平下的纯费率。通过分析，得到以下结论：

（1）大部分县市在Logistic、Weibull分布下拟合得比较好，有68个县市在这两个分布下的A-D检验值最小。从总体来看，Logistic分布拟合效果最好。

（2）非对称分布下的纯费率一般要高于对称分布，这是因为非对称分布更关注产量数据的尾部信息。

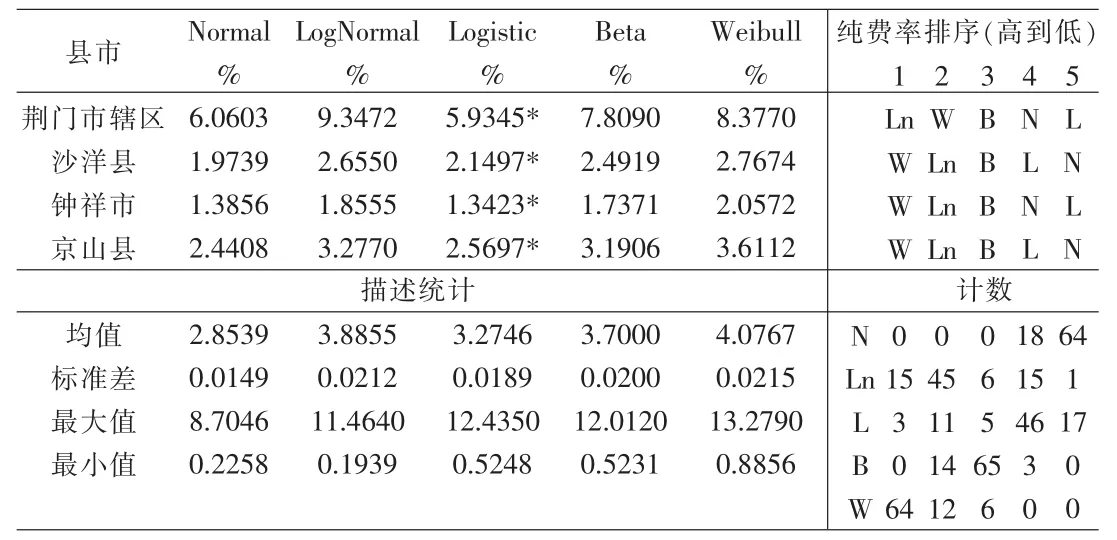
表3 湖北省县级水稻产量保险在各分布假设的纯费率的总体描述

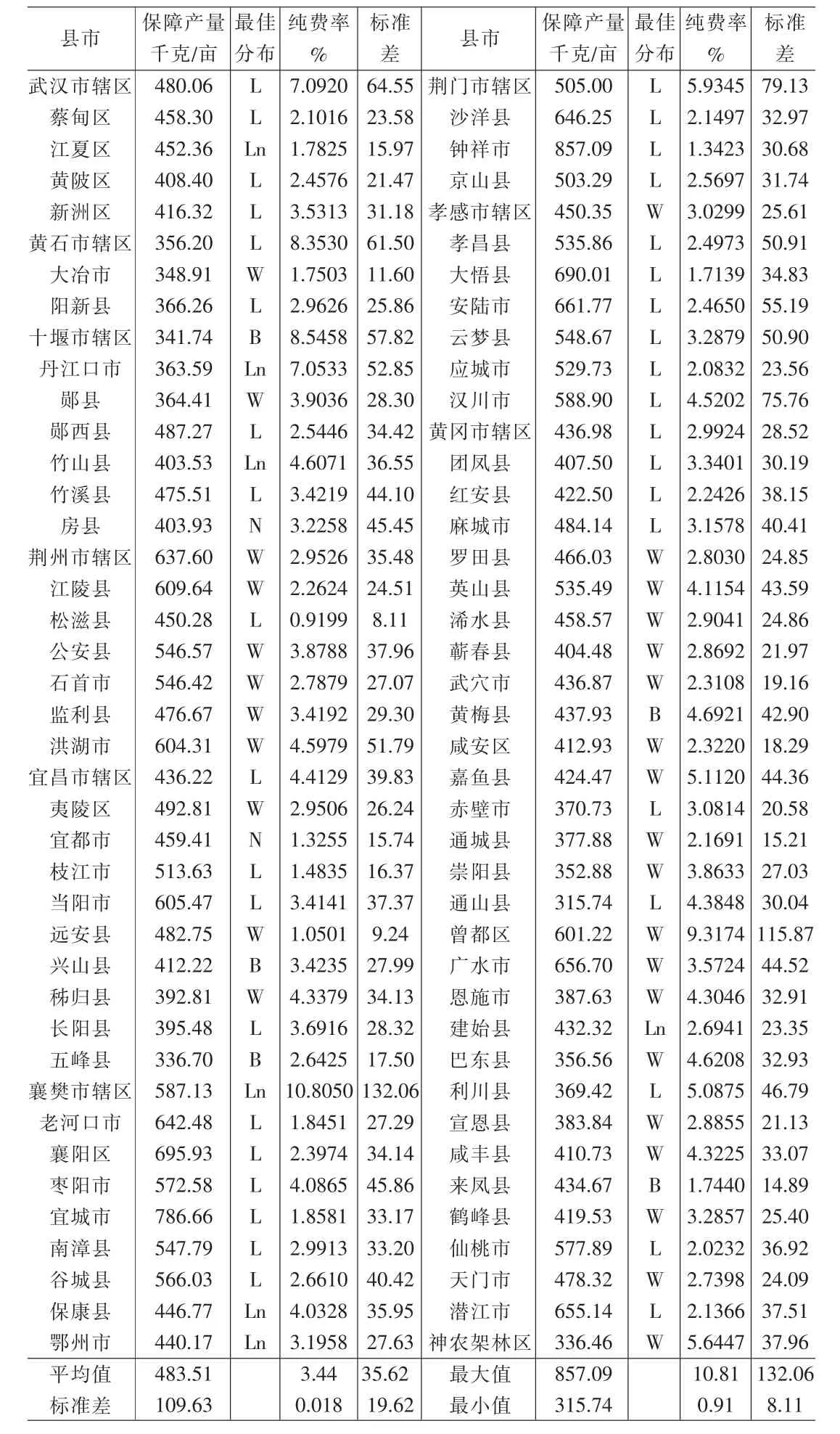
表4 湖北省县级水稻产量保险在最佳分布下的纯费率

（3）不同分布假设下的纯费率之间都有显著的差异，湖北省县级水稻产量保险纯费率的精确厘定依赖于产量分布的正确选择。

（4）最佳分布下的纯费率与样本数据标准差的Pearson相关系数为0.7873，说明纯费率可以较好地反映水稻的单产波动。

本文只选择了五种分布，并只使用Anderson-Darling（AD）检验值说明拟合情况，如何更好地评价所厘定的费率尚需进一步研究。湖北属于华中单双季稻稻作区，早、中、晚稻生产面临不同的风险，本文没有进行区分。另外，保险公司在提供农业保险时，一般不能保全部风险，但本文没有区分何种风险，针对一种或几种风险厘定费率值得进一步研究，但往往会受困于数据的缺乏。

[1]Day,R.H.Probability Distributions of Field Crop Yields[J].Journal of Farm Economics，1965，47.

[2]Gallagher,P.U.S.Soybean Yields:Estimation and Forecasting with Nonsymmetric Disturbances[J].American Journal of Agricultural Economics,1987,69.

[3]Goodwin,B.K.,A.P.Ker.Nonparametric Estimation of Crop Yield Distributions:Implications for Rating Group-Risk Crop Insurance Contracts[J].American Journal of Agricultural Economics,1998,80.

[4]Just,R.E.,Q.Weninger.Are Crop Yields Normally Distributed?[J].American Journal of Agricultural Economics,1999,81.

[5]Ker,A.P.,B.K.Goodwin.Nonparametric Estimation of Crop Insurance Rates Revisited[J].American Journal of Agricultural Economics,2000,83.

[6]Law,A.,W.D.Kelton.Simulation Modeling and Analysis.(3rdEdition)[M].New York:McGraw-Hill Higher Education,2000.

[7]Moss,C.B.,J.S.Shonkwiler.Estimating Yield Distributions with a Stochastic Trend and Nonnormal Errors[J].American Journal of Agricultural Economics,1993,75.

[8]Nelson,C.H.,P.V.Preckel.The Conditional Beta Distribution as a Stochastic Production Function[J].American Journal of A-gricultural Economics,1989,71.

[9]Ramírez,O.A.Estimation and Use of a Multivariate Parametric Model for Simulating Heteroskedastic,Correlated,Nonnormal Random Variables:The Case of Corn Belt Corn,Soybean and Wheat Yields[J].American Journal of Agricultural Economics,1997,79.

[10]Ramírez,O.A.S.Misra,J.Field.Crop Yield Distributions Revisited[J].American Journal of Agricultural Economics,2003,85.

[11]Roberts,R.A.J.Insurance of Crops in Developing Countries[M].FAO Agricultural Services Bulletin,2005.

[12]Sherrick,B.J.,F.C.Zanini,G.D.Schnitkey,S.H.Irwin.Crop Insurance Valuation under Alternative Yield Distributions[J].American Journal of Agricultural Economics,2004,86.

[13]Skees J.R.,Black J.R.,Barnett B.J.Designing and Rating an Area Yield Crop Insurance Contract[J].American Journal of Agricultural Economics,1997,79.

[14]Skees,J.R.,M.R.Reed.Rate-Making for Farm-Level Crop Insurance:Implications for Adverse Selection[J].American Journal of Agricultural Economics,1986,68.

[15]Skees,J R.,P.Hazell,M.Miranda.A New Approaches to Crop Yield Insurance in Developing Countries[C].International Food Policy Research Institute,EPTD Discussion Paper No.55,1999.

[16]Taylor C.R.Two Practical Procedures for Estimating Multivariate non Normal Probability Density Functions[J].American Journal of Agricultural Economics,1990,72.

[17]Turvey,C.,C.Zhao.Parametric and Nonparametric Crop Yield Distributions and their Effects on All-risk Crop Insurance Premiums[C].Working Paper,1999