一种简便的含裂纹梁的有限元模型

吴国荣，戎瑞亚，刘俊梅

(浙江海洋学院船舶与建筑工程学院，舟山 316004)

裂纹问题广泛存在于实际工程结构中，特别是岩体工程中的软弱结构面、结构工程及大型水工建筑物中的施工缝或开裂面、机械工程中的接触面和航天航空工程中复合材料的层面等均可能出现位移不连续现象，其中有些裂纹危及结构的安全，甚至导致突发的灾难性后果，因此，如何有效地识别和检测裂纹就具有十分重要的工程意义[1]。常见的裂纹识别方法有很多，如超声检测法、荧光剂检测、电涡流与声发射检测等,这些方法在裂纹检测上已取得了很好的效果，然而，这些传统的裂纹检测方法都存在着工艺复杂，难以定量分析等缺陷,很容易出现漏检和误判。基于振动特性的裂纹检测法作为一种在线的无损检测方法近年来越来越受到重视[2-7]。如何建立裂纹的力学模型准确计算裂纹对结构特性的影响是这种无损检测方法获得好的效果的前提条件。许多学者对此进行了大量的研究，从解析解、半解析解到数值计算方面提出一系列解决策略[8-10]。

本文研究了含常开裂纹梁的弯曲变形问题，建立起含裂纹的梁单元模型，基于断裂力学中的含裂纹梁的能量表达式，利用卡氏定理导出了含裂纹梁单元的柔度矩阵；基于力的平衡方程，利用柔度矩阵和刚度矩阵的物理含义导出了含裂纹梁单元的刚度矩阵。基于Matlab软件进行了数值模拟运算，给出了裂纹对梁挠度的影响。

1 柔度矩阵

对于含有裂纹的梁单元，由于裂纹处截面的转角不连续，要构造一个恰当的形函数是非常困难的。断裂力学对由于裂纹尖端的应力集中而引起的应变能的增加作了深入的研究，给出了其计算表达式。从而可以方便地导出含裂纹梁单元的柔度系数。

考虑一含裂纹梁单元，将右边的单元作为对含裂纹梁单元产生主动载荷，左边的单元则对其起固定约束作用，建立图1所示的悬臂梁模型。不考虑裂纹时，该梁单元的变形能为：

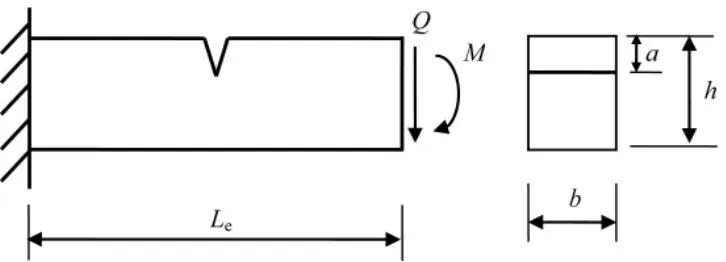
图1 含裂纹梁单元模型Fig.1 The model of the cracked beam element

其中，EI为梁的抗弯刚度，Q和M分别为右端截面上的剪力和弯矩，Le为单元的长度。对于矩形截面梁，由于裂纹而额外增加的变形能为：

式中，a和b分别为裂纹的深度和截面的宽度，ГⅠ和ГⅡ分别为与张开型和滑移型裂纹相对应的应力集中因子，其表达式分别为：

这里，a 为裂纹深度，b 和 h 分别为截面的宽和高，系数 ξ=a/h。函数 FⅠ(ξ)和 FⅡ(ξ)分别为[11]：

记C*为该梁单元的柔度矩阵，由卡氏定理，可得：

式中，

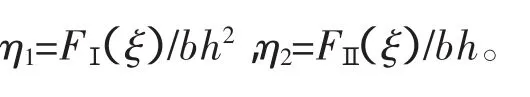
2 刚度矩阵

图 2 为一含裂纹梁单元，记 F=[Q(1)M(1)Q(2)M(2)]T和X=[v(1)θ(1)v(2)θ(2)]T分别为其节点载荷列阵和位移列阵。由力的平衡方程，可得：

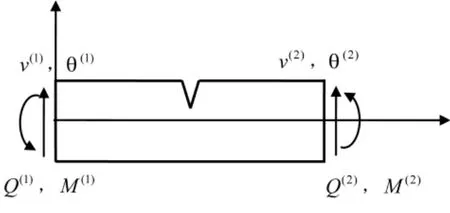
图2 含裂纹梁单元Fig.2 The cracked beam element

式中，

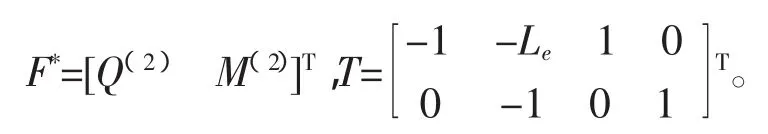
这里上标“T”表示矩阵的转置。注意到图1模型中对节点1处位移的约束，则有：

式中，

由柔度系数的物理含义，有：

由(9)式、(10)式和(11)式，可得：

其中

为含裂纹梁单元的刚度矩阵。当a=0时，则退化为：

这正是采用三次插值形函数的无裂纹梁单元刚度矩阵。

3 数值算例

分别就含常开裂纹的简支梁和悬臂梁进行了数值模拟运算。梁的几何尺寸及材料常数为：长L＝1.0 m、高h＝0.04 m及宽b＝0.02 m，弹性模量E=200 GPa。梁受一均布外载q=1.0 kN/m荷作用。表1给出的是无量纲最大挠度(最大挠度与无裂纹梁的比值)随裂纹深度的变化。表2和表3分别给出的是ξ=0.2时简支梁和悬臂梁的无量纲最大挠度随裂纹位置的变化。图3给出是ξ=0.2和无裂纹梁的挠曲线。图3和表1 ～3中的xc分别表示裂纹所在的位置对于简支梁为到支座的距离和对于悬臂梁为到固定端的距离。

表1 无量纲最大挠度随裂纹深度的变化Tab.1 The variation of the dimensionless deflection with the crack depth

表2 简支梁的无量纲最大挠度随裂纹位置的变化Tab.2 The variation of the dimensionless deflection with the crack position of the simple supported beam

表3 悬臂梁的无量纲最大挠度随裂纹位置的变化Tab.3 The variation of the dimensionless deflection with the crack position of the cantilever beam

图3 梁的挠曲线：实线为含裂纹梁，虚线为无裂纹梁Fig.3 The beam deflections:solid line for the cracked beam,dashed line for the uncracked beam

4 结论

本文提出了一种简便的含裂纹梁的有限元模型，基于断裂力学理论和力的平衡方程，利用柔度矩阵和刚度矩阵的物理含义，导出了含裂纹梁单元的刚度矩阵。分别就简支梁和悬臂梁进行了数值计算，从结果可以看出：随着裂纹深度的增加，挠度也随之增加；对于简支梁，裂纹在中间位置对挠度的影响最明显，对于悬臂梁，裂纹在根部位置影响最明显。

[1]范天佑.断裂理论基础[M].北京：科学出版社,2003.

[2]张敬芬,赵德有.工程结构裂纹损伤振动诊断的发展和展望[J].振动与冲击,2002,21(4):22-26.

[3]GEORGE D,GOUNARIS A,CHRIS A.Papadopoulos,Crack identi.cation in rotating shafts by coupled response measurements[J].Engineering Fracture Mechanics,2002(69):339-352.

[4]RIZOS P,ASPRAGATHOS N,DIMAROGONAS A.Identi.cation of crack location and magnitude in a cantilever beam from the vibration modes[J].Journal of Sound and Vibration,1990,138:381-388.

[5]李 兵,陈雪峰,胡 桥,等.基于小波有限元的悬臂梁裂纹识别[J].振动工程学报,2004,17(2):159-164.

[6]ZHENG D Y,FAN S C.Natural frequencies of a non-uniform beam with multiple cracks via modified Fourier series[J].Journal of Sound and Vibration,2001,242(4):701-717.

[7]ZHENG D Y,FAN S C,Natural frequency changes of a cracked Timoshenko beam by modified Fourier series[J].Journal of Sound and Vibration,2001,246(2):297–317.

[8]陈梦成,余荷根,汤任基.三维裂纹问题的高精度数值解法[J].固体力学学报,2002,23(2):207-211.

[9]尹 峰.关于表面裂纹理论的研究与进展(上)[J].沈阳航空工业学院学报,2003,20(3):88-91.

[10]BAMNIOS Y,DOUKA E,TROCHIDIS A,Crack identification in beam structures using mechanical impedance[J].Journal of Sound and Vibration,2002,256(2):287-297.

[11]NAHVI H,JABBARI M,Crack detection in beams using experimental modal data and finite element model[J].International Journal of Mechanical Sciences,2005,47(2):1 477-1 497.