改进Tent混沌序列的数字电路BIST技术
2010-07-18王石记杨春玲
朱 敏,王石记,杨春玲
(1.哈尔滨工业大学电气工程及自动化学院,哈尔滨 150001,zhuminhit@163.com;2北京航天测控技术开发公司,北京 100041)
改进Tent混沌序列的数字电路BIST技术
朱 敏1,王石记2,杨春玲1
(1.哈尔滨工业大学电气工程及自动化学院,哈尔滨 150001,zhuminhit@163.com;2北京航天测控技术开发公司,北京 100041)
针对目前数字电路规模变大,测试困难的特点,提出了一种基于改进Tent混沌序列的数字电路BIST技术.采用改进混沌Tent映射模型构建硬件电路并产生具有白噪声特性的“0-1”随机序列作为数字电路的自动测试生成图形,利用CRC特征电路分析输出响应,并得到混沌序列的测试响应特征码,通过特征码的不同来检测故障.研究表明,本文方法易于BIST技术实现,相比于普通M序列性能优越,能够得到更高的故障检测率和故障隔离率,适合于FPGA等大规模可编程逻辑电路的自动测试.
时序电路;Tent混沌0-1序列;内建自测试;循环冗余码
随着超大规模集成电路(VLSI)和可编程逻辑器件(PLD)的发展,一般的数字电子系统可以在单独的一片可编程芯片中实现.单片芯片所能实现复杂设计的提高和不断增长的设计复杂性,使得数字电路的测试变得越来越困难.其主要原因一是一般的数字电路都包括存储单元,即各种触发器、寄存器电路,这些记忆单元不易设定和检测,其可控性和可观测性差[1-4].二是系统复杂度增长的同时,芯片的输入输出接口相对较少,即可访问管脚的比重在下降.因此,在数字电子系统设计之初需要考虑测试问题,即可测性设计[5-6].
内建自测试(BIST)技术为数字电路测试提供了一种实用的可测性设计方案.内建自测试将测试激励产生(TPG)电路、测试控制电路和响应分析(ORA)电路都嵌入在原电路中[7-9].
本文提出的基于改进Tent混沌序列的数字电路BIST技术,即在数字电路系统中增加Tent混沌序列发生硬件电路作为自动测试图形生成电路,并采用CRC响应分析电路作为输出响应特征分析.文中给出了针对ISCAS’85标准测试组合逻辑电路c17和ISCAS’89标准测试时序电路s27的测试结果.研究表明,本文提出的方法易于BIST技术的实现,可应用于一般的数字逻辑电路,包括FPGA等VLSI的内核功能的自动测试.
1 改进Tent混沌序列数字电路BIST技术
1.1 改进的Tent映射混沌特性分析
Tent映射模型[10-12]:

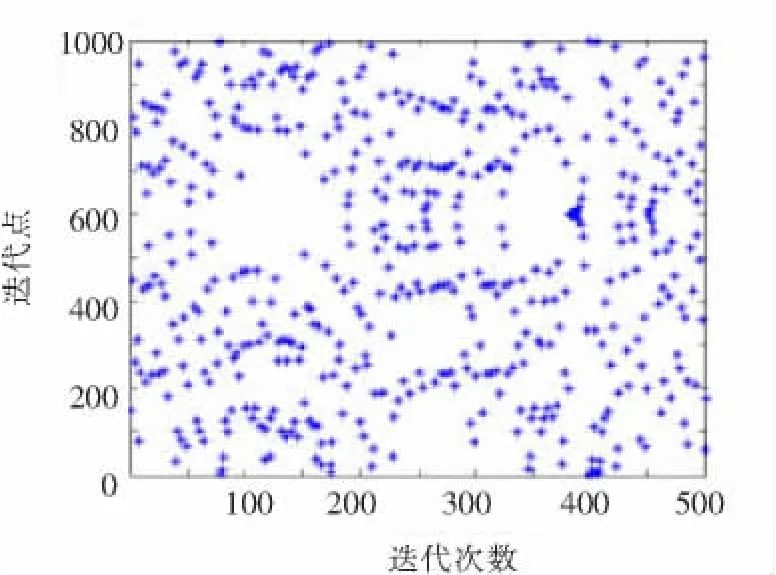
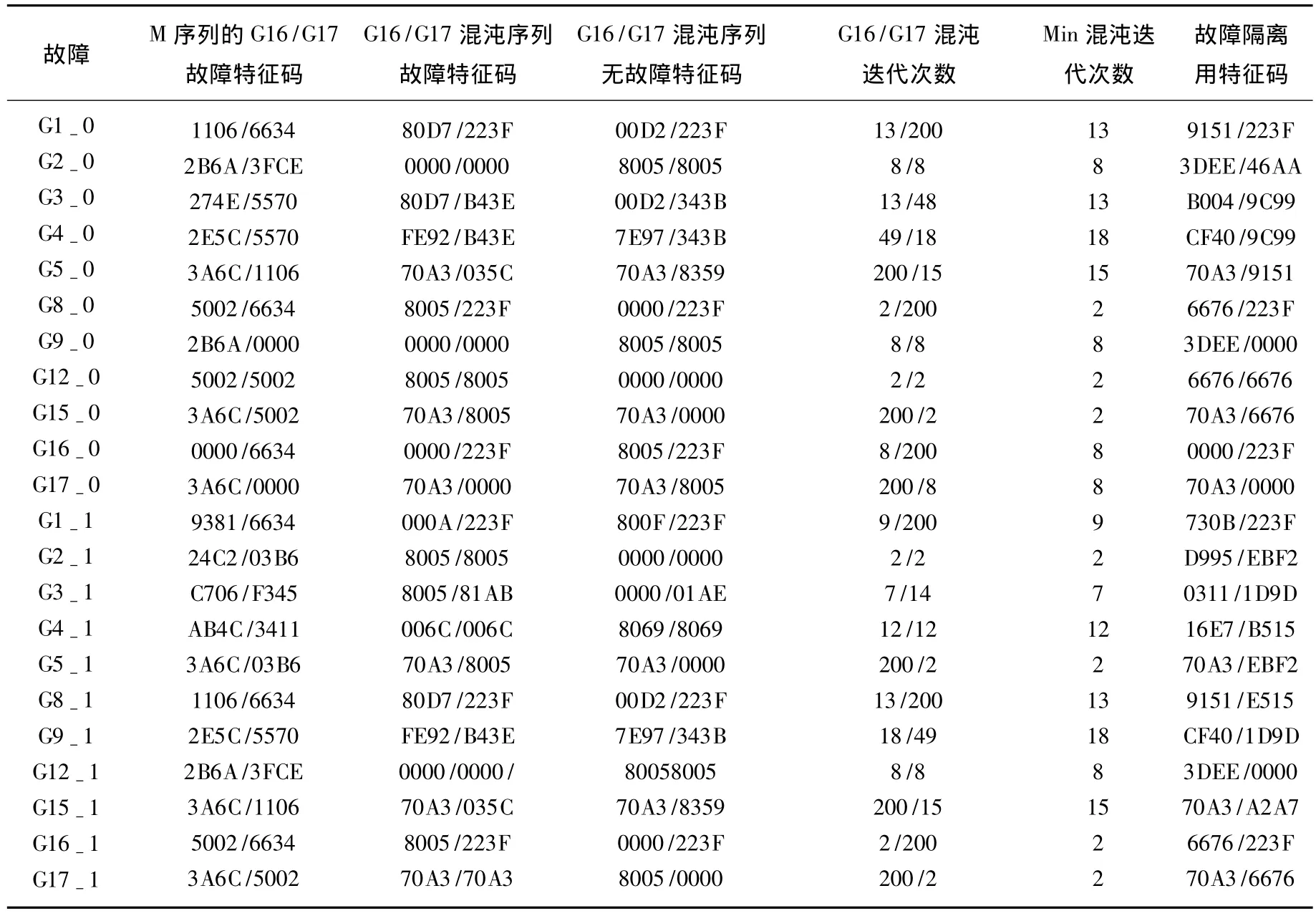
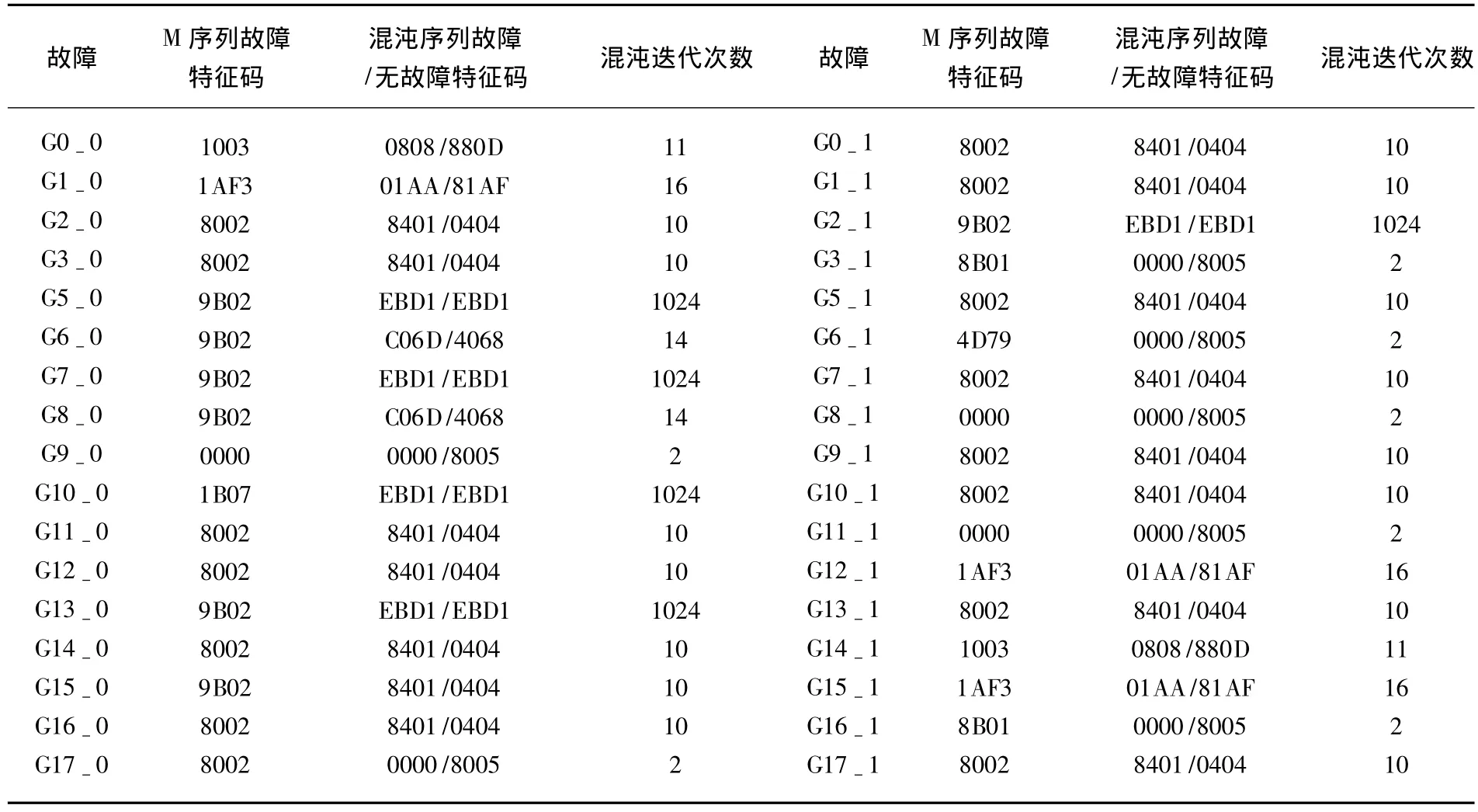
其中0 为便于硬件电路的实现,本文将Tent映射混沌序列进行改进,其迭代公式为 上述改进型Tent混沌迭代的初始值x0= 150,迭代500次的映射过程如图1所示. 图1 初始值为150的改进Tent混沌映射过程 图2 改进Tent映射的随机特性 图2为初值x0= 150,迭代次数为500的Tent混沌模型的随机特性图.可以看出Tent混沌模型迭代值遍历( 0,999)空间,说明其具有很好的随机特性.图3为初值相差10-11时,在迭代大约50次后,两个混沌序列X1,X2将完全不同.因此可以看出,只要初值稍加修改,就可得到完全不同的序列.因此,本文提出的改进的Tent混沌序列能产生比M序列更多更为广泛应用的随机序列. 图3 改进Tent映射初值相差10-11时迭代图 考虑到FPGA内核电路是纯数字电路,并结合Tent混沌序列的上述特性,所加的测试激励需要为“0 -1”序列[13-15],本文改进 Tent映射,得到改进的混沌Tent映射模型的“0-1”随机序列. 由于改进Tent映射迭代值在( 0,999)空间是遍历的且均匀分布,因此改进的“0-1”混沌序列中“0”和“1”分布也是均匀的,满足Golomb提出的随机序列公设条件中0和1均衡分布的条件.序列的自相关函数为 式(4)中si与si+k是由同一初值所产生的相差K个间隔点数的序列.式(5)中si与s′i+K是不同初值所产生的相差K个间隔点数的序列.图4(a)为改进Tent混沌二进制序列的自相关特性图,序列的初始值为x0= 150,图中间隔K从0到2 000,序列长度为5 000.图4(b)为改进Tent混沌互相关特性图,序列分别是由初始值x0=150和x0=151所产生的不同序列之间互相关性仿真. 本文提出的基于改进的Tent混沌序列的“0-1”随机序列具有非常好的自相关和互相关特性,其自相关特性类似于δ函数,具有白噪声的特性,且互相关值非常小,特性也接近于白噪声.结合混沌序列的初值敏感性,只需要改变初值就可以产生特性很好的任意长度的随机序列,这种特性适合作为数字电路的自动测试图形生成电路. 图4 “0-1”随机序列的自相关性与互相关性 本文利用改进的Tent混沌映射在FPGA中实现BIST测试,其结构框图如图5所示. 图5 数字系统实现BIST结构框图 图中混沌算法测试图形生成电路采用改进的Tent混沌映射迭代算法.利用硬件描述语言实现式(2)中的迭代运算.为节省硬件资源,式中的乘法运算可以通过移位运算和加减运算来实现.算法描述如下: Step1:初始化,x(i)取初始值x0; Step2:if(x(i)≥333),则x(i+1)=1499-x(i)-(x(i)≫1),进入Step 4,否则进入Step3;(其中“≫”表示右移操作.) Step3:x(i+1)=(x(i)≪1)+x(i);(其中“≪”表示左移操作.) Step4:将当前的x(i+1)赋值给下一次迭代运算的x(i); Step5:判断是否到指定的迭代次数N,如果是就结束运行,并输出x(i),其中i=1, 2,…N,否则返回Step2继续执行. 将混沌算法产生的序列加载在被测电路CUT(Circuits Under Test)的输入端,在CUT的输出端得到响应序列.利用数据通信中CRC校验数据传输的原理,将CRC作为响应特征分析电路,其硬件通过线性反馈移位寄存器(LFSR)来实现. 以标准组合测试电路ISCAS’85中的c17作为被测电路,Tent混沌迭代算法作为测试图形生成电路,CRC电路用于响应分析.被测电路有5个输入端 G 1,G 2,G 3,G 4,G 5,2 个输出端 G16 和G 17,中间节点G 8,G 9,G 12,G 15,其混沌迭代电路BIST的结构如图6所示. 图6 混沌测试电路BIST结构框图 混沌测试图形生成电路是由混沌算法所构建的硬件电路.在测试使能信号test-en和系统时钟clk的作用下,测试控制状态机产生激励时钟信号clk-out,将产生的混沌序列通过移位寄存器串行移入被测数字电路的输入端.同时通过控制信号sel控制MUX选择测试激励,切断正常数据通道data-in.此时混沌序列激励信号加载在被测电路c17的输入端,并在输出端读出响应,暂存在寄存器中.在测试控制控制状态机的控制下输入到CRC电路中进行分析并输出结果. 被测电路的每个节点分别可以设置固定为“0”和“1”的故障,其中 G5-0 和 G5-1分别表示节点G5发生固定为“0”和“1”的故障,依此类推.采用CRC多项式x16+x2+1作为响应分析电路,得到相应的特征码.经过若干次的迭代,特征码输出将不同,测试结果见表1. 表1中给出了分别以LFSR产生的M序列和混沌序列作为测试激励矢量,在输出端G16和G17采用CRC响应分析电路得到的特征码.M序列的无故障特征码为“3A6C/6634”,混沌序列的迭代次数不同故障特征码也不同,分别将其列于表中.可以看出,利用LFSR所产生的M序列和混沌序列都能达到100%检测故障的目的,混沌序列检测所有故障的迭代次数为18次,比M序列长度要短.经过足够的迭代次数其故障隔离率能达到90.9%,远大于M序列45.5%的隔离率. 表1 c17测试结果 标准时序测试电路ISCAS’89中的s27包含一个时钟控制端CK和4个信号输入端G 0,G 1,G 2,G3和一个可观测输出端G17等17个节点,因此共有34个故障.与组合电路不同的是时序电路的输入激励需要保持被测时序电路时钟的20个周期,以确保时序电路有足够的时钟周期进行状态转换. 表2给出了s27的测试结果.其中响应输出采用CRC多项式x16+x2+1作为响应分析.表中M序列的无故障特征码为“9B02”,因此可计算出M序列作为测试激励的故障检测率为27/34=79.41%,而 Tent混沌迭代序列最大可达85.29%.表3给出了针对s27不同迭代次数故障检测率的关系.通过实验验证,s27的G2-1,G5-0,G7-0,G10-0 和 G13-0 等 5 个故障为冗余故障,无法检测.又由于混沌序列具有初值敏感性,即改变初值能够产生完全不同的随机序列,因此,在某些情况下可以通过施加不同的混沌序列作为测试激励来提高故障的检测率. 表2 s27测试结果 表3 s27混沌迭代次数与检测率关系 提出了一种基于改进的Tent混沌序列的数字电路BIST技术.该方法通过混沌Tent模型映射生成随机序列,并构建硬件电路作为BIST的测试图形生成电路,通过CRC响应特征分析电路给出故障相应的特征码.实验研究表明本文提出的改进Tent混沌序列具有良好的随机特性,在经过很少的迭代次数就能产生很高的故障检测率和故障隔离率.所提出的方法适合于一般的数字逻辑电路以及FPGA等VLSI的内核功能的自动测试. [1] FUJIWARA H.A new class of sequential circuits with combinational test generation complexity[J].IEEE Transactions on Computers, 2000,49(9):895-904. [2] YEEOOI C,FUJIWARA H.A new class of sequential circuits with acyclic test generation complexity[C]//International Conference on Computer Design.San Jose:San Jose′State University,2007:425 -431. [3] HIKEUNG T,SRINIVAS D,NEWTON R A,el al.Test generation for sequential circuits[J].IEEE,Transaction on Ransation on Computer-Aided Design, 1988,7(10):1081-1092. [4] FU M.Minimal memory inverses of linear sequential circuits[J].IEEE Transactions on Computers, 1974,C-23(11):1155-1163. [5] 顾德均.航空电子装备修理理论与技术[M].北京:国防工业出版社,2001:19-20. [6] 丁瑾.可靠性与可测性分析设计[M].北京:北京邮电出版社,1996:106-118. [7] SCHOTTEN C,MYER H.Test-point insertion for an area-efficient BIST[C]//Proceedings of International Test Conference.Washington,DC:Aachen Univ of Technol,1995:515 -523. [8] CHEN C,GUPTA S K.A methodology to design efficient BIST test pattern generations[C]//Proceedings of International Test Conference.Washington,DC:IEEE Computer Society,1995:814-823. [9] AHMAD A A,MITR S,MCCLUSKEY E J.BIST reseeding with very few seeds[C]//VLSI Test Symposium.California:Center for Reliable Comput,Stanford Univ,2003:69-74. [10]JESSA M.The period of sequences generated by tentlike maps[J].IEEE Transactions on Circuits and Systems——I:FundamentalTheoryandApplications, 2002,49(1):84 -89. [11]STOJANOVSKI T,KOCAREV L.Chaos-based random number generators-part I:analysis[J].Analysis.IEEE Transaction on circuits and systems——I:Fundamental theory and applications, 2001,48(3):281-288. [12]STOJANOVSKI T,PIHL J,KOCAREV L.Chaosbased random number generators-part II:practical realization[J].IEEE Transaction on circuits and systems——I:Fundamental theory and applications, 2001,48(3):382-385. [13]KATZ O,RAMON D A,WAGNER I A.A robust random number generator based on a differential currentmode chaos[J].IEEE Transactions on very large scale integration(VLSI)systems, 2008,16(12):1677 -1686. [14]BULS J.Construction of pseudo-random sequences from chaos[C]//COC,St.Petersburg:Univ of Latvia,2000:558-560. [15]JESSA M.Combined pseudochaotic psudorandom generator[C]//ICSES 2008 International conference on signals and electronic systems.Krakow:Poznan Univ of Technol,2008:257 -260. BIST technique of digital circuits based on improved tent chaotic sequence ZHU Min1,WANG Shi-ji2,YANG Chun-ling1 (1.School of Electrical Engineering and Automation,Harbin Institute of Technology,Harbin 150001,China,zhuminhit@163.com;2.Aerospace Measurement& Contro,Beijing 100041,China) This paper proposed a realization method of BIST technique of digital circuits based on improved Tent chaotic sequence to address the problem of testing digital circuits.Random sequence of“0 -1”with white noise characteristics which generated by improved tent chaotic logistic map model hardware implementation is used as automatic test pattern generation(ATPG)of digital circuits.Test response signatures of chaotic sequence are obtained from CRC analysis of output response.It is shown that the method presented in this paper is easy for realization of BIST and has superior performance of higher rate of fault detection and fault isolation than that of M sequence.It is suitable for large-scale FPGA and automatic testing of other programmable logic circuits. sequential circuits;tent chaotic 0-1 sequence;BIST;CRC TP702 A 0367-6234(2010)04-0607-05 2009-12-07. 国家自然科学基金资助项目(60877065);哈尔滨市科 技创新人才研究专项资金(RC2008XK009004). 朱 敏(1981—),男,博士研究生; 杨春玲(1965—),女,教授,博士生导师. (编辑 赵丽莹)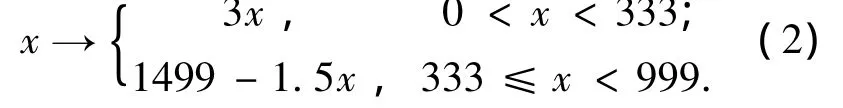



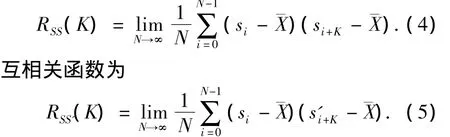

1.2 改进Tent混沌映射的硬件电路BIST技术实现

2 实验及分析
2.1 组合电路测试分析

2.2 时序电路测试分析

3 结语
