螺栓球节点试验及在单层网壳结构中的应用性

曹正罡，范 峰，马会环，王 伟

(哈尔滨工业大学土木工程学院，哈尔滨 150090，caohit@hit.edu.cn)

螺栓球节点试验及在单层网壳结构中的应用性

曹正罡，范 峰，马会环，王 伟

(哈尔滨工业大学土木工程学院，哈尔滨 150090，caohit@hit.edu.cn)

为充分利用螺栓球节点的抗弯刚度，实现其在单层网壳结构中的应用，针对螺栓球节点开展力学试验研究，配合以精细化的有限元分析，获得节点的抗弯性能，并采用弯矩－转角关系来描述.利用ANSYS程序，采用弹簧单元模拟节点弯曲与扭转性能并将试验获得的弯矩－转角关系引入节点属性中，构建了螺栓球节点单层网壳的有限元模型.在此基础上系统开展了网壳结构的稳定性能研究.结果显示:采用螺栓球节点的网壳对于荷载不对称分布较为敏感，而且失稳过程中总伴随有节点的弯折效应;单层球面网壳的极限承载力最低可达到对应刚性节点网壳的32%，最高则超过98%，而单层柱面网壳则仅为10%，这表明此类节点可以应用在单层球面网壳中，但不宜在单层柱面网壳中采用.

单层网壳;螺栓球;承载力;试验

螺栓球节点外型美观，安装便捷，非常适合应用在网架、网壳结构中.但从安全性角度考虑，空间网格技术规程(JGJ61－2003)［1］中规定将螺栓球节点假设成铰接节点，忽略其抗弯刚度，并建议仅在双层网壳中使用.因此，我国也仅在一些小跨度或作为维护结构的单层网壳中应用有螺栓球节点［2］，从构造和受力特点分析，螺栓球节点实际具有一定的抗弯能力，应属于半刚性节点.如果能够充分利用螺栓球节点的抗弯刚度，将其应用在中等跨度以上的单层网壳结构中，将极大地提高单层网壳结构安装精度并提高施工效率.

国外对于新型螺栓连接节点的应用要比我国广泛，开展的研究也较为深入.英国研究人员对于各种新型螺栓连接节点的构造进行了总结和分类［3］，日本 Kato 等［4－6］以及西班牙 López［7］则对螺栓球节点网壳的分析方法以及倒塌机理开展了较为系统的研究.我国在实际工程中尚未利用螺栓球的抗弯能力，基于这一研究现状，必须对螺栓球节点的抗弯承载力、节点破坏机理以及在单层网壳结构中的应用性等关键性问题开展深入研究.

1 节点试验与有限元模拟

1.1 节点试验研究

试验目的在于螺栓球节点的抗弯性能，具体规格见表1［8］.试验中分级加载直至试件出现较大的塑性变形.

表1 螺栓球节点各部分的尺寸及材料特性

试验中应变片布置如图1所示.用电阻应变法来测量千斤顶施加在球面顶端的力，采用TS3860电阻应变仪，电阻应变片的型号为BX120－3AA，灵敏度系数为2.05±0.1%.为了消除试验过程中偏心受力和温度引起的误差，在所有测点的正反两面各布置一片应变片，将两片应变片串联后与温度补偿片接成半桥电路进行测试;节点位移采用百分表进行测试.试验构件及加载设备布置如图2(a)－(b)所示.

图1 加载试件图

在加载的过程中，所有试件的变形过程相似.以M24螺栓球节点为例，当锥头与套筒接触面处弯矩达到1.03 kN·m时，套筒与锥头之间、套筒与球体间的接触面的下端开始出现缝隙，加载过程中，接触面下端的缝隙逐渐增大，见图2(c)，当弯矩增大到2.10 kN·m时，缝隙不再增大，弯矩增长也变的缓慢.显然套筒边缘由于挤压作用、螺栓由于弯曲作用均已开始进入塑性;图2(d)可以清晰地显示出螺栓最终的弯曲变形.套筒表面则始终处于受压状态，而且压力持续增大，当弯矩值接近1.0 kN·m时，套筒表面就已经进入塑性.

图2 试验加载图与配件变形图

通过对试验过程的跟踪测量，可以获得节点外部弯矩与杆件转角关系曲线，共计9组试验.由于其中一组加载失败，未获得完整曲线，其中M27螺栓3组试验曲线与节点转角计算简图如图3所示.曲线变化规律基本一致.初始阶段，由于试件处于弹性阶段，曲线几乎呈直线型，达到某一具体值后，转角急剧增大，而弯矩增加趋势减缓，试件进入塑性状态的特征较为明显，这也可通过套筒表面压应力数值变化得出，本文限于篇幅未列出对应的应力曲线.

1.2 节点有限元分析与试验结果对比

通过试验完全可以准确获得节点抗弯性能，但实际工程中节点域内的球径、螺栓直径、杆件直径以及套筒、锥头等配件的组合变化较多，少量试验结果无法满足工程需要，必须建立有效的有限元分析方法，以开展更多系列的螺栓球节点抗弯性能研究.利用ANSYS软件中的SOLID45实体单元来模拟螺栓球的各部分构件(图4(a)－(b))，材料本构采用理想弹塑性模型，屈服应力均按表1中数值假设.选用表面接触单元和目标单元来模拟部件之间接触(接触模拟法).接触单元覆盖于三维实体的表面，当单元表面渗透到目标面上时，接触就发生.接触面布置位置与接触面上变形分布情况如图4(c)－(d)所示.

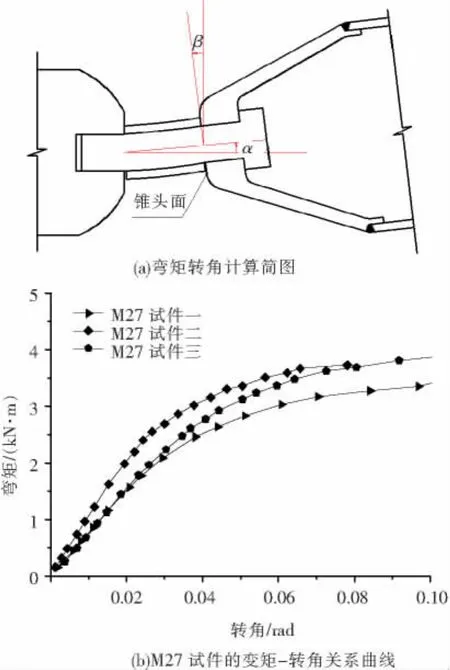
图3 节点转角定义与试验获得的弯矩－转角关系

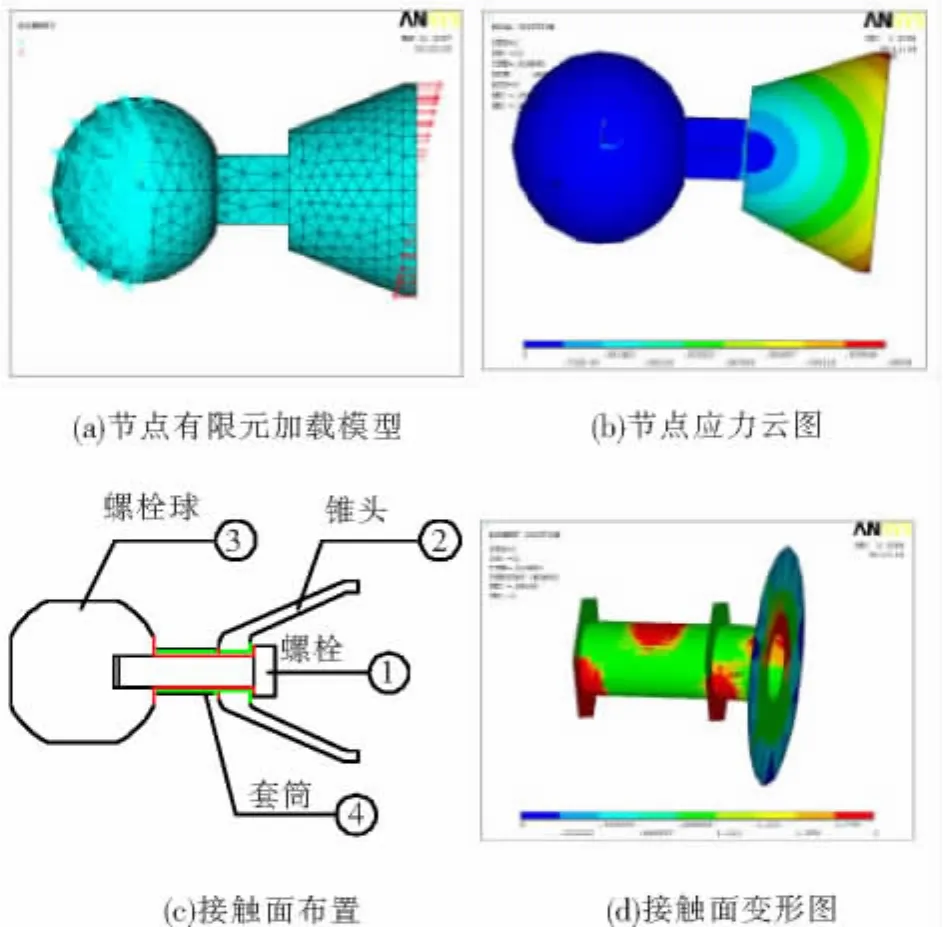
图4 螺栓球节点有限元模型与响应云图

同试验分组一致，分别模拟装配有 M20、M24、M27三种螺栓直径球节点的抗弯试验，各部分尺寸严格保证与试验数据一致，同样选取锥头处绘制其弯矩－转角曲线.

图5中列出了具有代表性的M24螺栓球节点试验与数值模拟获得的弯矩－转角曲线.可以看出，试验与数值模拟获得的屈服弯矩大体相同，曲线在弹性阶段数据吻合较好;而在弹塑性阶段曲线发生一些偏离，分析主要原因:1)试验本身制作和安装误差;2)材料本构与实际属性存在偏差;3)测量误差.其中第2方面应是导致两者曲线偏差较大的主要原因.

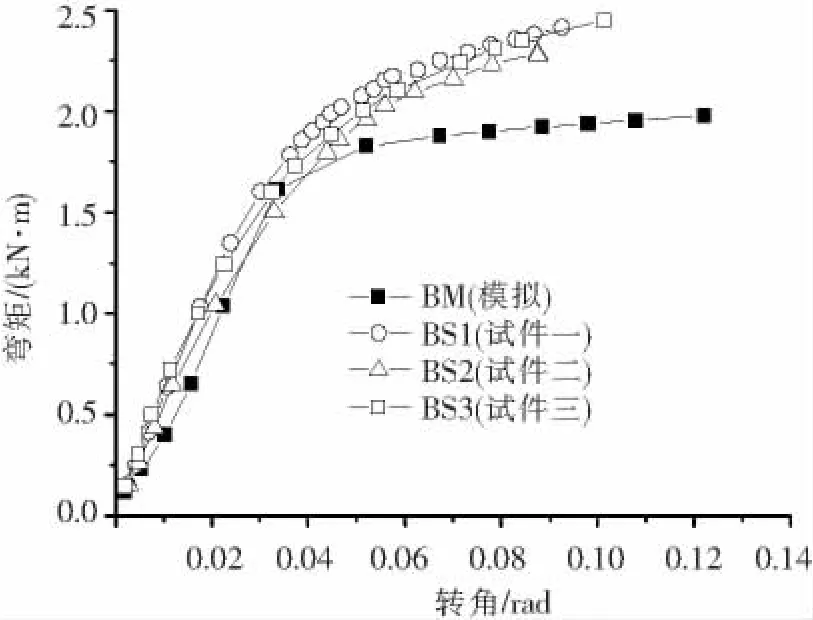
图5 节点试验与有限元模拟结果对比

1.3 螺栓球节点网壳的有限元建模

将节点抗弯性能转化到网壳整体模型中可以应用的方法有变刚度法、分段等效刚度法［9］等.本文通过引入combin39弹簧单元，其特点是可以利用实常数将试验获得的弯曲－转角关系直接引入到单元属性中;而每个螺栓用3个弹簧单元代替，通过变换局部坐标系，使其分别代表扭转刚度和两向抗弯刚度(图6(a))，同时将节点域与杆件端部的三向线位移耦合一致，既可以模拟螺栓球节点的受力特征［10］.这一方法的特点:1)杆件端部的扭转与抗弯刚度相互独立;2)可以直接引入节点试验或数值模拟的结果;3)不同直径螺栓可以对应不同的弯矩－转角关系.

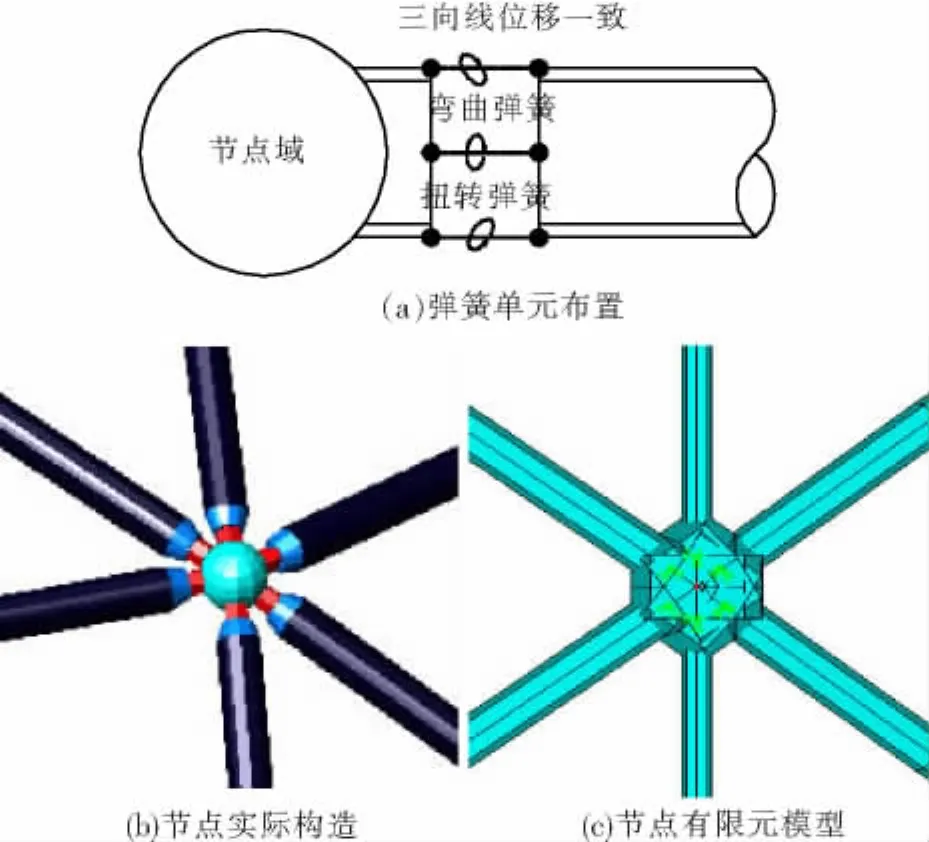
图6 螺栓球网壳中节点模拟图

对于球体的模拟，采用在节点域内将杆件截面适当放大，从而保证节点域的刚度远大于杆件刚度(图6(b)－(c)).网壳杆件采用beam189梁元模拟，并均假设为理想弹塑性材料.

2 螺栓球节点球面网壳的稳定性分析

基于以上建模技术与试验结果，重点针对应用范围较广的K6型单层球面网壳开展稳定性研究，网壳全部杆件均采用114×4.0 mm圆管.

2.1 屈曲模态

以往研究表明，传统刚性节点单层球面网壳的屈曲模态往往表现为局部节点的凹陷;而当节点刚度接近铰接状态时，网壳的屈曲模态表现为壳面节点的扭转(图7(a));当杆件－节点之间采用M20－M27螺栓连接时，网壳屈曲模态也均表现为节点的凹陷，宏观上与刚接网壳基本一致，但通过局部区域的放大显示可知，在螺栓球节点域连接处发生了弯折现象(图7(b)).

2.2 扭转刚度的影响

传统设计中一致认为螺栓球节点扭转刚度很小，而在单层网壳结构中，节点的扭转刚度对整体极限承载力会产生什么样的影响尚无定论.为此采用M24型球节点网壳，重点研究节点具有不同扭转刚度对网壳极限承载力的影响.扭转刚度取初始扭转刚度的 1/ 100，1/ 10， 1， 10，100 倍(初始扭转刚度取节点实际弯曲刚度的1/100)，极限荷载随扭转刚度系数的变化曲线如图8所示.显然，各种矢跨比情况下，极限荷载随网壳扭转刚度的变化不大，节点的扭转刚度对极限荷载影响很小.按计算结果统计，此差别的平均值为0.4%.因此可以认为节点扭转刚度对球面网壳极限荷载的影响可忽略不计.

对于蚁群算法的特征而言，比较方便和适用的是信息传递模型 Message Passing Interface（MPI），该软件平台无关于编程语言，进行并行计算只需调用MPI的可移植性编程接口即可实现，也可进行异步通信，能应用于目前流行的各大操作系统，易于操作和实现。设定有r只蚂蚁，划分q为个子蚁群，在各处理器中各子任务分别执行串行蚁群算法。

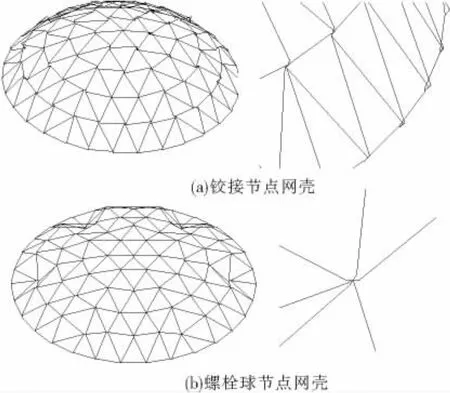
图7 不同节点刚度球面网壳的屈曲模态

图8 极限荷载随节点扭转刚度的变化曲线

表2 具有不同节点弯曲刚度球面网壳的极限荷载比值ζ

2.3 弯曲刚度的影响

同样，开展节点不同弯曲刚度对球面网壳极限承载力的影响研究.螺栓选取试验中用到的M20、M24、M 27，节点的扭转刚度实际弯曲刚度的1/ 100，网壳的跨度分别取30 m和40 m.同时为对比，还分析了铰接和刚接节点两种极端情况.

经过对分析结果的统计，将获得的不同跨度、矢跨比下，不同节点弯曲刚度时的极限荷载与刚接单层网壳承载力的比值ζ列于表2中.从表格中可以清晰的看到，K6型螺栓球节点网壳的极限承载力多数情况下是铰接网壳的3倍多，更接近于刚接网壳.而且矢跨比越大，螺栓球节点网壳的极限荷载越接近于刚接网壳.显然随着矢跨比的增大，网壳薄膜受力状态越明显，杆件主要以承受轴向力为主，节点弯曲刚度的影响也就逐渐减小.对于表中个别数值大于1.0的现象应是计算误差导致的，不具有代表意义.宏观统计的结果表明，螺栓球节点球面网壳应属于一种典型的半刚性节点的网壳，具有较高的极限承载能力.

2.4 不对称荷载作用的影响

对于荷载不均匀分布的影响，主要考虑了活载与恒载的比例分别为p/g= 0，1/ 4，1/2的情况(p为活荷载;g为恒荷载)，荷载分布形式如图9所示.网壳结构的极限荷载均以总荷载(p+g)作为衡量指标.

图9 网壳不对称荷载分布图

由图10看出，球面网壳的极限荷载基本上随着活载比例的增大而降低.当p/g=0.5时，极限荷载值平均降低到均布荷载作用情况下的75%，显然荷载的不对称分布导致了壳面内薄膜受力状态的改变，局部网壳由于受力不均就会稍许倾斜，薄膜受力状态很快地转向弯曲受力状态，导致节点承受的弯矩增大，且这种效应随着不对称荷载的比例增大而越加明显.

图10 极限荷载随不同比例不对称荷载作用的变化曲线

同样，荷载的不对称分布也将导致球面网壳失稳模态的改变，图11给出了螺栓直径为M24的螺栓球节点网壳在不对称荷载作用下的屈曲模态.在活载分布的一侧，壳面发生较大面积的凹陷，而仅有恒荷载作用的一侧，壳面则基本保持完整.这种屈曲模态与刚接球面网壳差异较大，刚接球面网壳往往是在活荷载作用一侧发生局部的节点凹陷.由极限荷载与屈曲模态的分析表明，螺栓球节点球面网壳对于不对称荷载分布的敏感性要远高于刚接网壳.

图11 不对称荷载作用下的网壳屈曲模态

3 螺栓球节点柱面网壳的稳定性分析

上述分析表明，螺栓球节点完全可以应用在单层球面网壳工程中，但这一结论是否能在其它类型网壳中同样适用，需要开展更多形式螺栓球节点网壳结构的稳定性能研究.限于篇幅，这里仅对采用三角形网格，约束条件为两纵边支承和四边支承，跨度均为15 m的单层柱面网壳结构开展研究，获得此类节点柱面网壳的基本力学性能.

3.1 屈曲模态

图12 螺栓球节点域变形图

3.2 极限承载力分析

针对两种约束条件下的柱面网壳进行极限承载力分析，如图13所示.结果与球面网壳结论大不相同，刚接节点柱面网壳的极限承载力远远大于三种螺栓球节点情况，平均相差5倍以上，而且这种差别在两种约束条件下也基本保持不变，显然螺栓球节点并不适用于单层柱面网壳结构中.分析其原因，主要是柱面网壳结构的受力机理与球面网壳差异较大，球面网壳结构的受力基本上是以薄膜力为主，杆件主要承受轴向力，弯矩作用较小，因此对节点的抗弯刚度要求较低.而单层柱面网壳在跨度方向呈圆拱受力特点，以薄膜力为主;而在长度方向构件布置基本与外荷载垂直，以弯曲受力为主，这样将对节点的弯曲刚度要求较高，因此会导致螺栓球节点柱面网壳的极限承载力明显偏低.尝试将3种螺栓球节点的抗弯刚度提高100倍，获得极限荷载则明显得到提升，甚至与刚性节点情况比较接近.

由此可见装配有螺栓球节点的单层柱面网壳不宜在实际工程中采用，但这也不完全否定螺栓球柱面网壳的承载能力，因为它仍具有一定的承载能力而非机构，这样对于承受荷载较小的装饰性结构中尚可考虑使用，但应充分核算其实际承载能力.

图13 柱面网壳极限荷载随节点弯曲刚度变化曲线

4 结论

1)采用接触模拟法建立的螺栓球节点数值模拟方法，可以在一定条件下替代试验研究，获得与试验结果较为接近的螺栓球节点的抗弯性能.

2)利用弹簧单元，引入螺栓球节点的弯矩－转角关系，可以模拟网壳结构中螺栓节点抗弯性能，实现螺栓球节点网壳结构的有限元建模.

3)节点抗弯试验表明，螺栓球结点具有一定的抗弯刚度，属于半刚性节点，网壳结构设计中将其假设成铰接节点，偏于保守.

4)螺栓球节点网壳屈曲模态中节点连接处弯折现象严重，表明螺栓球节点弯曲刚度对网壳结构极限承载力起到控制作用，而扭转刚度的影响可以忽略不计.

5)螺栓球节点球面网壳对于荷载的不对称分布较为敏感，以球面网壳为例，当p/g为1/2时，网壳的极限承载力平均降低到均布荷载情况的75%.

6)螺栓球节点球面网壳极限荷载最低可达刚接节点网壳的36%，最高可超过98%，因此螺栓球节点可以在一定范围内应用在单层球面网壳中.而柱面网壳中杆件弯矩较大，螺栓球节点柱面网壳的极限承载力偏低，平均值仅为刚接节点网壳的10%，表明螺栓球节点不适用于柱面网壳结构.

［1］ JGJ61－2003网壳结构技术规程［S］.北京:中国建筑工业出版社，2003:17－20.

［2］ 赵宪忠，沈祖炎，陈以一，等.上海东方明珠国际会议中心单层球网壳整体模型试验研究［J］.建筑结构学报， 2000，21(3):16－22.

［3］ CHENAGHLOU M R.Semi－ Rigidity of Connection in Space Structure［D］.Guildford:University of Surrey，1997.

［4］ KATO S，MUTOH I，SHOMURA M.Collapse of semi－rigidly jointed reticulated domes with initial geometric imperfections［J］.Journal of Constructional Steel Research， 1998，48:145－168.

［5］ UEKI T，KUBODERA I，KATO S.Single－layer lattice domes using systematized semi－ rigid joints［C］//Proceedings of the 40th anniversary congress of IASS.Madrid:［s.n.］，1999:69－76.

［6］ SHIBBATA R，KATO S，YAMADA S.Experimental Study on the Ultimate Strength of Single Layer Reticular Domes［C］//Proceeding of the Fourth International Conference of Space Structure.Guildford:University of Surrey，1993:389－396.

［7］ LÓPEZ A，PUENTE I，SERNA M A.Numerical model and experimental tests on single-layer latticed domes with semi-rigid joints ［J］.Computers and Structures， 2007，85:360 －374.

［8］ 马会环.半刚性节点单层球面网壳稳定性分析［D］.哈尔滨:哈尔滨工业大学，2007.

［9］ 郭小农，沈祖炎.半刚性节点单层球面网壳整体稳定性分析［J］.四川建筑科学研究， 2004，30(3):10－12.

［10］ 范峰，曹正罡，崔美艳.半刚性节点单层球面网壳弹塑性稳定性分析［J］.哈尔滨工业大学学报， 2009，41(3):10 －15.

Experiment of bolt-ball joint and its application in single-layer reticulated shells

CAO Zheng-gang，FAN Feng，MA Hui-huan，WANG Wei

(School of Civil Engineering，Harbin Institute of Technology，Harbin 150090，China，caohit@hit.edu.cn)

The bolt-ball joint system with actual bend-bearing capacity can be used in single-layer reticulated domes.Both experimental study and sophisticated finite element analysis were carried out to obtain the bending capacity of the joint which was described by bending-rotation curves.The finite element model of a single-layer reticulated dome with bolt-ball joints was established by ANSYS，in which spring elements were used to simulate bending stiffness of the joint obtained experimentally.The stability of single-layer domes was analyzed.Results indicate that the single-layer dome with bolt-ball joints is sensible to asymmetry load distribution and its buckling is process always accompanied with bending of the joint.The critical load of a single-reticulated dome with bolt-ball joints is 32%as that of much as the rigid dome at least，and the percentage will be over 98%at most.But for a single-layer cylindrical reticulated dome，the percentage is only 10%，indicating that the bolt-ball joint system can be used in single-layer reticulated domes，but should not be used in a single-layer cylindrical reticulated dome.

single-layer reticulated dome;bolt-ball joint;bearing capacity;experiment

TU393.3

A

0367－6234(2010)04－0525－06

2009－03－13.

中国博士后科学基金资助项目(20070420876);

国家自然科学基金资助项目(50778054).

曹正罡(1975—)，男，博士，讲师;

范 峰(1971—)，男，教授，博士生导师;

王 伟(1957—)，男，教授，博士生导师.

(编辑 赵丽莹)