畸变图像的有效配准算法

王 华，丛建亭，侯相深，孙金玮

(1.哈尔滨工业大学交通科学与工程学院，哈尔滨 150090，hitwh@hit.edu.cn;2.哈尔滨工业大学电气工程及自动化学院，哈尔滨 150001)

畸变图像的有效配准算法

王 华1，丛建亭2，侯相深1，孙金玮2

(1.哈尔滨工业大学交通科学与工程学院，哈尔滨 150090，hitwh@hit.edu.cn;2.哈尔滨工业大学电气工程及自动化学院，哈尔滨 150001)

镜头畸变是导致图像质量降低的主要因素之一.通常在图像存在畸变情况时，要先通过图像畸变校正方法来减小畸变对图像的影响，但校正过程较为复杂.本文提出了一种新的畸变图像的有效配准算法，算法分为初始匹配和松弛优化匹配两步，初始匹配算法采用圆投影匹配算法，松弛匹配算法则以向量旋转角的旋转和缩放不变性特征作为初始匹配对的优化准则，首先计算向量旋转角度差值，然后通过构造支持度函数和剔除策略选出最优匹配对.实验证明，该算法在图像非线性畸变误差较大的情况下也能够实现正确匹配.

图像畸变;圆投影匹配;向量旋转角;松弛匹配

图像配准是医学、航空、模式识别和图像拼接等领域的一项极其重要的技术［1］，因此一直以来都是图像处理领域中的热点问题之一，几十年来关于图像配准的各种算法也层出不穷［2－5］，但是很多算法在图像质量降低的时候会失效.

目前图像拼接面临的难题主要集中在图像配准这一关键环节，虽然国内外许多学者对该环节进行了广泛和深入的研究，并且针对不同类型的图像也提出了很多有效的方法，但是仍然存在以下几个方面的问题［2］:(1)目前的研究成果仍然无法实现全自动的图像配准;(2)由于图像噪声的影响、获取景物区域和边缘的困难以及缺乏必需的控制特征点等因素的限制，高精度的图像配准难度很大;(3)如何提高配准处理速度，达到快速和实时的要求也是图像配准的一大难题;(4)在参考图像与待配准图像之间有较大的尺寸比例差别、较大的旋转角及较大的平移时的情况时，常常会出现配准失效的现象;(5)目前的图像拼接的评价主要依托于图像配准与图像融合的评价体系，而它们的评价方法至今也没有一种公认的统一的评价方法，进而导致了图像拼接方法的各个性能的不一致性.

由于镜头畸变是导致图像质量降低的主要因素之一［3］，通常在图像存在畸变情况时，要先通过图像畸变校正方法来减小畸变对图像的影响，校正过程较为复杂，因此本文提出了一种新的畸变图像配准算法并对算法的抗畸变性能通过标准图像作了详细的研究.

1 图像的非线性畸变理论

相机成像过程中产生的非线性变形主要取决于镜头镜片组合间距误差，其次是镜片本身的曲线误差和CCD的制造误差.上述的各项因素产生的非线性变形综合效果可以用数学模型［4］来表示

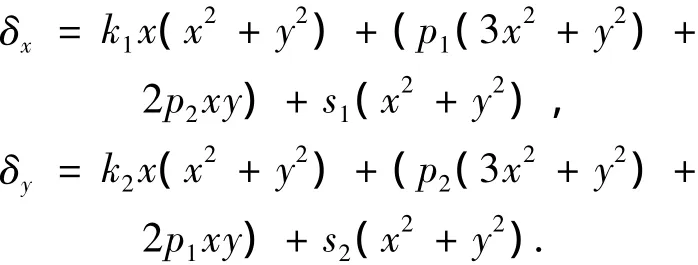
式中:δx、δy分别为图像像素点在图像坐标系中x、y方向的变形量;x、y分别是图像坐标系中的像素点的坐标;k1、k2、p1、p2、s1、s2分别为变形系数.上式中的变形量可分为三部分，第一部分称为径向畸变，第二部分称为离心畸变，第三部分称为薄棱镜畸变.一般在应用中仅取第一部分的畸变，这部分的变形已经足够描述非线性畸变［4］.由此可得

式中r2=x2+y2，x′和y′分别是与实际图像中的坐标为x和y相对应的变形校正后的坐标.

2 图像匹配算法的相关理论

2.1 Moravec兴趣点

Moravec兴趣点［5］是指一幅图像内在水平、垂直及两个对角线方向灰度变化最小的一类特征点，具有计算简单和速度快的优点.其实现步骤［6］:

(1)计算各个像素的兴趣值IV，以像素点g(x，y)为中心取w×w(如5×5的窗口)，按式(1)计算其沿水平、垂直及两个对角线方向的灰度变化(如图1所示).

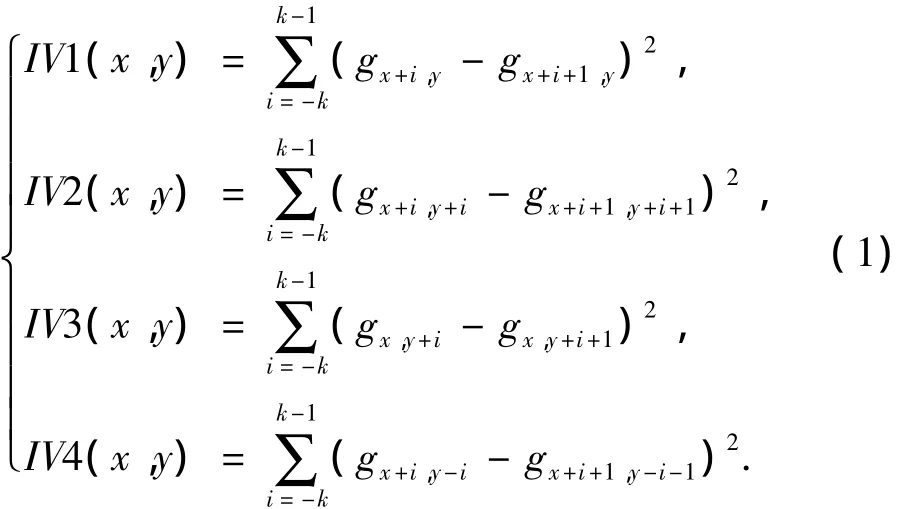
式中，k=INT(w/2).取4个方向的最小者作为像素点g(x，y)的兴趣值IV(x，y):

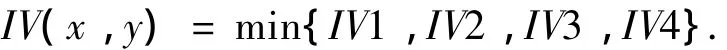
(2)给定一个经验阈值T，将兴趣值大于T的点作为候选点.

(3)在一定大小的窗口内(可不同于兴趣值计算窗口)，候选点中兴趣值最大的像素点即作为兴趣点.

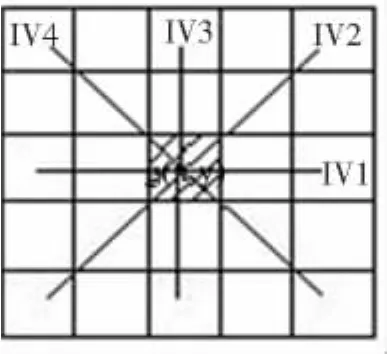
图1 Moravec算子5×5窗口

2.2 圆投影初始匹配算法

本文采用了圆投影匹配算法对Moravec兴趣点做初始匹配.采用极坐标表示参考图像T，以图像T中提取出的M点为坐标原点O，建立极坐标系，如图2所示.设O在原坐标系中的坐标为(Φ，Ψ)，图像中的像素在原坐标系中的坐标为(m，n)，则定义圆投影向量P(r)为

图2 计算圆投影向量

当图像旋转时，任一半径圆上的像素也跟着作同心同半径旋转，所以P(r)是保持不变的，因此P(r)是一个旋转不变量.圆投影匹配算法就是以圆投影向量为基础实现匹配的，因而能实现任意角度旋转的正确匹配［7］.

以PT(r)表示参考图像的圆投影向量，PSi，j(r)表示待配准图像子图Si，j的圆投影向量.定义相似性度量函数为

由于图像在计算机中是以矩阵形式存储的，(R，θ)与(r，θ)所对应的点通常会落在图像像素之间，采用就近原则选取像点往往会造成一些像素的重复选择和漏取，而且计算也非常麻烦，若将圆拉成正方形环如图3所示，每个环都是以坐标原点O为中心，则投影图既包含了图像的所有信息，计算也很简单［8］.

图3 环投影

2.3 基于向量旋转角的四元松弛匹配优化算法

假设参考图像1、待配准图像2的初始匹配后的点特征集P={p1，p2，…，pm}和Q={q1，q2，…，qm}，其中，P可以看作Q经过平移后迭加一定的畸变误差而得到的对应点集，点集中存在一定比例的错误匹配对(注:一般情况下，错误比例不超过 60%)，(pi，qi)、(pj，qj)和(pu，qu)为集合中任意3个初始匹配对.

提出一种新的抗畸变的松弛优化匹配算法，其主要思想及实现过程如下:对每一特征点四元组(pi，qi，ph，qh)，首先要计算出参考图像 1 和待配准图像 2 中点对(pu，qu)与(pi，qi，ph，qh)构成的向量旋转角度差θ.

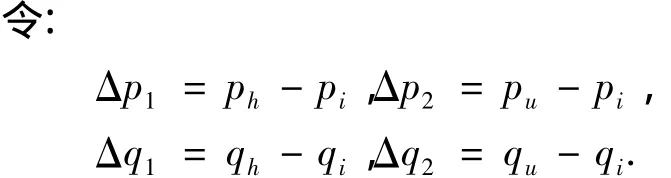
则由四元组 (pi，qi，ph，qh)可求得在pi与qi配对且ph与qh配对的情况下(如图4所示)，向量Δp2与向量Δp1的夹角θ1，向量Δq2与向量Δq1的夹角θ2的标量值分别为

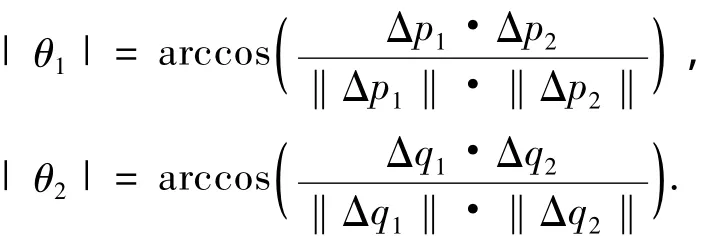
则待配准图像2中向量角θ2与参考图像1中向量角θ1的角度差θ为

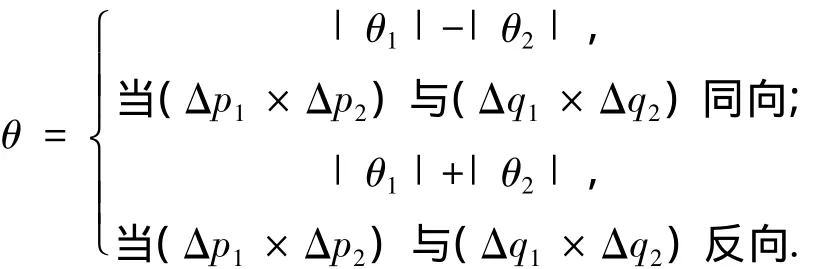
这里，(Δp1×Δp2)与(Δq1×Δq2)均表示两向量的向量外积的方向向量.

令 φiihh(u，u)为(pu，qu)对四元组(pi，qi，ph，qh)的支持度函数.

角度差θ的变化范围为(－π，π)，类似基本点松弛匹配算法的支持度函数形式，构造一个基于θ的支持度函数

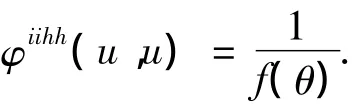
其中f(θ)是与畸变误差相关的支持基函数，基函数的形式可根据图像畸变误差的大小选择不同的函数形式.

当畸变误差较小时可选基于tan(k·θ)的函数来提高支持度函数对θ变化的敏感度.

在畸变误差范围确定的条件下，可以通过选取某个函数来调整算法对畸变的容忍度.

式中:a表示畸变误差容忍指数函数ax的底数;θr表示点集的畸变误差在期望情况下的θ容忍余量;θm表示点集的畸变误差在最坏情况下的θ容忍余量，即θ值得信赖的上限.实验证明，a取值在1＜a＜1.3时效果较好，∞可取非常大的值.

假如f(θ)=1，表明向量旋转角θ1与θ2相等，则表示qu相对于qi和qh相似于pu相对于pi与ph，因此点对(pu，qu)应当给予四元组(pi，qi，ph，qh)以最大的支持，随着f(θ)的增加，其支持度应减小.

四元组(pi，qi，ph，qh)周围的点对对它的最大支持度可以表示为

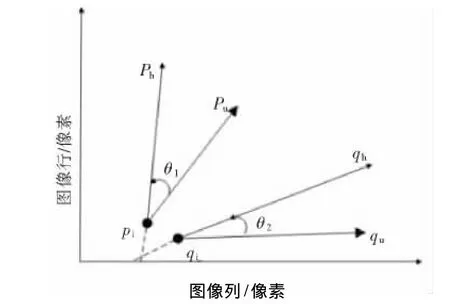
图4 基于向量角的旋转与比例不变示意图

如果(pu，qu)与图像中其他匹配对组成的任意四元组的最大支持度都不大，则可以认为(pu，qu)是错误匹配对，应该剔除掉.因此在优化过程中可设置平均支持度阈值，当(pu，qu)与图像中其他匹配对组成的任意四元组的最大支持度的平均值(即(pu，qu)的平均支持度)大于该阈值，则认为匹配对(pu，qu)为正确匹配对.

3 实验结果

从USC－SIPI图像数据库网站下载512×512的Lena图像作为配准实验的参考图像(图5(a))，并对参考图像作桶形畸变与枕形畸变变换，如图5(b)和图5(c)所示.

图5 Lena参考图像及其两种畸变图像

经多次反复实验，本算法对在不同畸变系数下的桶形畸变图像配准和枕形畸变图像配准的正确匹配率平均统计图如图6所示.当畸变系数k取0

图6 桶形畸变和枕形畸变图像配准统计

本文实验只取畸变系数k=k1=k2=±2×10－6两种情况时，当系数绝对值超过此值时图像畸变将明显影响人的主观视觉感受.从参考图像与待配准图像中均匀提取150个左右的Moravec兴趣点，反复实验证明，Lena图的圆投影初始匹配阈值和平均支持度阈值设置在0.99以上较为合理，因此将初始匹配阈值设置为0.995可筛选出若干错误比例小于60%的初始匹配对集.平均支持度阈值主要用来控制优化后匹配对的数目，反复实验证明，Lena图的平均支持度阈值在0.99以上比较合理.经过四元松弛匹配优化算法后，大于阈值0.99的所有匹配对均保留下来作为正确匹配对(注:也可以根据需要的匹配对个数优化).实验中支持基函数f(θ)选用第2节公式(2)，本文实验中a=1. 1，∞取10 000，θr取经验值0. 45，θm取经验值0.6.

4 结果分析

图7(a)是参考图像与桶形畸变图像的圆投影初始匹配结果，由于受畸变误差影响，结果中存在大约40%的错误匹配对，从图7(b)可以看出，经过四元松弛匹配优化算法错误匹配对被全部剔除.同样从图8也可以看出，本算法对枕形畸变图像也有效.

当图像存在畸变误差时，本算法通过选用支持度基函数式(2)，可以正确优化匹配对.由于该算法支持度函数的衰减速度是随着畸变误差的不同而相应改变，因此在已知畸变误差范围的情况下，可以通过调整参数θr和θm来合理改变不同畸变误差情况下的支持度衰减速度从而使算法对畸变误差有较强的容忍能力，也就可以区分正确匹配对与错误匹配对.值得一提的是，平均支持度的阈值要根据实际需要合理选取，通过图8(c)可看出，当平均支持度阈值选取为0.95时出现了两个错误匹配对1和 2，这说明为了避免正确匹配对大量丢失的同时也容忍了少量的错误匹配对，但是错误匹配对的衰减速度相对正确匹配对来说仍然快得多，因此只要根据实际需要的匹配对数目合理优化，这些错误匹配对一般都会被剔除掉.

图7 参考图像与桶形畸变图像的初始和优化匹配对

图8 参考图像与枕形畸变图像的初始匹配对和平均支持度阈值分别为0.99与0.95的优化匹配对

5 结语

提出了一种新的畸变图像配准算法，首先均匀提取Moravec兴趣点，然后通过圆投影匹配算法对兴趣点初始匹配，最后根据基于向量旋转角的四元松弛匹配优化算法对初始匹配进行筛选优化得到正确匹配对.反复实验证明，本算法在畸变图像之间存在旋转、缩放和畸变误差情况下，通过调整支持基函数f(θ)的形式，可使算法对存在较大畸变误差的图像配准具有一定的容忍能力.

［1］王蕾，刘贵喜.图像配准技术及应用研究［D］.西安:西安电子科技大学，2007.

［2］倪国强，刘琼.多源图像配准技术分析与展望［J］.光电工程， 2004，31(9):1 －6.

［3］朱铮涛，黎绍发.镜头畸变及其校正技术［J］.光学技术， 2005，31(1):136－141.

［4］姜大志，郁倩，王冰洋，等.计算机视觉成象的非线性畸变研究与综述［J］.计算机工程， 2001，27(12):108－110.

［5］MORAVEC H P.Towards automatic visual obstacle avoidance［C］//Proceedings of the 5th International Joint Conference on Artificial Intelligence.Cambridege，Massachusetts:The International Joint Conferences on Artificial Intelligence，1977:584.

［6］李晓娟，郭宝龙.图像拼接技术研究［D］.西安:西安电子科技大学，2007.

［7］徐亦斌，王敬东，李鹏.基于圆投影向量的景象匹配方法研究［J］.系统工程与电子技术， 2005，27(10):1725－1728.

［8］黄玲玲，吴庆宪，姜长生，等.巡航导弹航迹控制中景象匹配快速算法研究［J］.航空兵器，2006(5):43－48.

Effective matching algorithm of distorted images

WANG Hua1，CONG Jian-ting2，HOU Xiang-shen1，SUN Jin-wei2

(1.School of Transportation Science and Engineering，Harbin Institute of Technology，Harbin 150090，China，hitwh@hit.edu.cn;2.Department of Automatic Measurement and Control，Harbin Institute of Technology，Harbin 150001，China)

The image distortion caused by lens reduces the quality of images and the processing of image correction is complex.A new effective matching algorithm of distorted images is proposed in this paper，which has two steps of the initial matching and the relaxation optimization matching.The circular projection method is applied in the initial matching step and the algorithm with characteristics of anti-rotation and anti-scale of rotating angle of vectors is applied as the optimization criterion of matching pairs.The value difference of the rotating angle of vectors should be calculated at first，and then the optimal matching pairs can be selected by using of the support function and the rules of rejection.Experimental results with a large number of images prove that the algorithm is still effective in the condition of large nonlinear distortion error of images.

image distortion;circular projection matching;rotating angle of vectors;relaxation matching

TP391.41

A

0367－6234(2010)04－0597－05

2009－06－10.

王 华(1975—)男，博士，副教授.

(编辑 赵丽莹)