塑料包装材料化学物向食品迁移的模拟
2010-07-17李友爱
李友爱
(北京工商大学 计算机与信息工程学院, 北京 100048)
1 问题的提出
由于具有抗腐蚀能力强、不与酸碱反应、制造成本低、防水、质轻、容易被塑制成不同形状等众多优点,塑料已经被广泛地应用于食品和药品包装. 但是这些塑料包装材料中所含有的化学物可能迁移到被包装的食品和药品中,因而会危害人体健康. 如何检测和分析塑料包装材料化学物的迁移并形成相关的理论,已经成为食品和药品包装领域一个重要的研究课题. 目前,主要检测和分析手段是实验的方法. 然而,化学物迁移实验对实验仪器要求非常高,且实验复杂、费用昂贵,很难在普通的实验室完成. 因此,很多国内外的研究者将研究的重点向理论研究转移,其中的一个研究热点就是将化学物的迁移转化为一个微分方程,然后通过求解这一微分方程模拟化学物的迁移.
大量科学实验表明(Figge[1],Chang[2], Till等[3]), 当化学物在塑料内的扩散系数D以及它在塑料薄膜—食品间的分配系数K已知时,可基于Fick第二定律对迁移过程进行预测. 通常认为迁移仅发生在包装材料厚度方向上,可用一维二阶偏微分方程式
(1)
描述. 若扩散系数D与浓度无关,则上式简化为
(2)
对于上述迁移模型,只有在如下特殊的情况下才有可能求得解析解[4]:1)初始时刻,化学物均匀分布在包装薄膜中;2)化学物从包装薄膜一侧进入食品,交界面处没有传质阻力(传质系数 很大);3)任一时刻食品中的化学物均匀分布;4)在整个迁移过程中,扩散系数D和分配系数KP/F=CP,e/CF,e为常数;5)迁移过程任何时刻,在包装薄膜和食品的界面上都是平衡的; 6)忽略包装材料边界效应及其与食品的相互作用. 一般情况下,我们无法获得解析方法而只能借助于数 值方法.
对于模型(2),常用的空间离散方法有有限差分[5]、有限元[6]和有限体积方法. 对空间离散后,在时间方向的离散常用的有显式格式和隐式格式. 用显式格式计算简单,但是为了保证数值稳定性,时间步长必须较小;而用隐式格式计算时,可取较长的时间步长,但计算量要大得多. 并且这些方法有个共同的缺点,即时间步长相对较小,且精度不是很高. 钟万勰等在文献[7]中提出了一种精细时程积分法. 这种方法的一个显著特点就是具有高精度. 本文的目的是将精细时程积分法推广应用到化学物迁移模型(2)并给出误差分.
2 精细时程积分法
一般而言,化学物迁移模型(2)经过空间半离散后将得到如下关于时间的常微分方程组:
(3)
其中,v为浓度态变量,H为常系数矩阵,r为非齐次项,表示系统外部作用量. 方程(3)的解v因非齐次项r(t) 而分为两部分:v1和v2,即
v(t)=v1(t)+v2(t),
(4)
v1(t)=exp(Ht)·v0,
(5)

(6)
其中v0为初始条件.则该系统的解在时刻tk为

(7)
根据方程(7), 解在时刻tk+1(τ=tk+1-tk, 其中τ为时间步长) 为

(8)
通过推导vk和vk+1的关系,可得逐步积分公式

(9)
式(9)为精细积分法的基本公式,是基于解析方法导出的,将初始条件代入上式,即可逐步求出系统在各时刻的解,精细积分法的关键是计算上式中的指数矩阵
(10)
为简单起见,应用二阶Taylor展开计算上式中括号内的部分,得
(11)
其中
在式(11)中,高阶的Taylor展开值得推荐,会提高结果的精度. 注意到 Δt很小,故Tα相对于I也很小. 如果直接将他们累加会导致有效数位的很大损失. 有鉴于此,精确积分算法先将值较小的矩阵Tα累加,然后将之加到矩阵I. 注意到
(I+Tα)2=I+2Tα+Tα×Tα,
(12)
算法设计为
for (iter=0;iter (13) 当循环结束后, T=I+Tα. (14) 方程(13)和(14)是PTI计算指数矩阵(10)的关键步骤. 若r(t)=0,则方程(3)简化为 (15) H为常系数矩阵,其通解可形式地写成 v=exp(H·τ)v0, (16) 其中v0为初始时刻的值. 令T=exp(H·τ)=[exp(H·τ/m)]m,又令Δt=τ/m,m=2N(在文献[7]中,取N=20),则 T=[exp(H·Δt)]m. 令A=exp(H·Δt)≈I+HΔt+(HΔt)2/2!. 下面考察用精细时程积分法来近似精确解的误差. 不妨假定H对称负定,λ1,…,λn为H的特征值,且λi≤0. 又设|λ1|≤|λ2|≤…≤|λn|, 则 H=Qdiag(λ1,…,λn)QT, (17) 且QQT=I. 令vh=Amv0,于是误差为 v-vh=(exp(H·τ)-Am)v0= (18) exp(λ1Δt)=1+λ1Δt+(λ1Δt)2/2!+ (19) 即 1+λ1Δt+(λ1Δt)2/2! =exp(λ1Δt)- (20) 由方程(20)及(18)可知 Δ1=exp(λ1τ)-(1+λ1Δt+(λ1Δt)2/2!)m= (21) 其中x=-exp(λ1(Δξ1-Δt))(λ1Δt)3/3!. 利用一阶Taylor展开可得 (1+x)m=1+m(1+y1)m-1x, 0 (22) 从式(22)可知和(21)式, 可得 Δ1=-exp(λ1τ)m(1+y1)m-1x= (23) 下面依次考察式(23)中各项. 由于 0 exp(λ1τ)(1+y1)m-1= (24) 因为Δt=τ/m,λ1<0, 假设|λ1|≤|λ2|≤…≤|λn| 由上知,(24)式为 (25) 将(25)式代入(23)式得 Δ1≤exp(λ1Δξ1)|(λ1Δt)3/3!|. (26) 定理1 设v为方程(15)精确解,vh为用精细时程积分法得到的近似解, 则v-vh的l2误差为 ‖v-vh‖l2≤max1≤i≤ncexp(λiΔξi)|λi/m|3τ3‖v0‖l2, (27) 其中λi,i=1,2,…,n为矩阵A的特征值,m=2N,τ为时间步长,v0为初始时刻的值. 证明:在式(18)的两边左乘QT,令u=QT(v-vh),并注意到Q为正交矩阵,则 u=QT(v-vh)=diag(Δ1,Δ2, …,Δn)QTv0. (28) 令 y=QTv0=(y1,…,yn)T, (29) 则 u=diag(Δ1,Δ2, …,Δn)y. (30) 于是u的离散l2范数为 (31) 因Q为正交矩阵,故有 (32) ‖v-vh‖l2=‖u‖l2, (33) 即 ‖v-vh‖l2≤max1≤i≤n(Δi)‖v0‖l2. (34) 于是有 ‖v-vh‖l2≤ (35) 其中i=1,…,n,c表示不同的常数.3 精细时程积分法的误差估计
Qdiag(Δ1,Δ2,…,Δn)QTv0,
exp(λ1Δξ1)(λ1Δt)3/3!,
0 <Δξ1<Δt,
exp(λ1Δξ1)(λ1Δt)3/3!.
exp(λ1τ) -(exp(λ1Δt)-
exp(λ1Δξ1)(λ1Δt)3/3!)m=
exp(λ1τ) -exp(λ1Δtm)(1-
exp(λ1(Δξ1-Δt))(λ1Δt)3/3!)m=
exp(λ1τ)-exp(λ1τ)(1+x)m=
exp(λ1τ)[1-(1+x)m],
-exp(λ1τ)m(1+y1)m-1(-exp(λ1(Δξ1-
Δt))(λ1Δt)3/3!)=
exp(λ1τ)exp(λ1(Δξ1-Δt))m(1+
y1)m-1(λ1Δt)3/3!=
exp(λ1(Δξ1-Δt))mexp(λ1τ)(1+
y1)m-1(λ1Δt)3/3!.
exp(λ1Δt)(exp(λ1Δt)+exp(λ1Δt)y1)m-1≤
exp(λ1Δt)(exp(λ1Δt)-
exp(λ1Δξ1)(λ1Δt)3/3!)m-1=
exp(λ1Δt)(1+λ1Δt+(λ1Δt)2/2!)m-1.

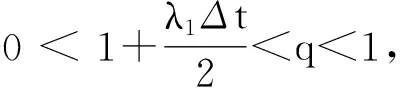


max1≤i≤ncexp(λiΔξi)|λi/m|3τ3‖v0‖l2,
