柱面件无压边多点成形中成形面的修正与回弹控制

陈喜娣



柱面件无压边多点成形中成形面的修正与回弹控制

陈喜娣

（五邑大学 机电工程学院，广东 江门 529020）

利用数值模拟技术，在回弹分析的基础上，研究了不同厚度的柱面件在无压边多点成形中回弹影响的修正方法. 结果表明：目标曲面成形件依据最后一次修正的成形面调整基本体群的形状进行多点成形，可以有效补偿板材的回弹影响，并能实现板材的精确成形.

多点成形；柱面件；数值模拟；回弹控制

多点成形[1]利用一系列高度可调的基本体群自由地构造成形曲面，使板材成形为需要的零件，具有无模、快速和柔性成形的特点. 无压边多点成形主要以面外弯曲变形为主，其板材面内变形力较小，通常用于变形量不大的曲面成形，但回弹对成形件最终形状的影响比有压边成形的大. 由于回弹的存在，板材成形时，若严格按照目标曲面调整基本体群成形面将无法得到所需零件的几何形状，因此必须根据回弹的分布规律，对由基本体冲头群构成的成形面的形状进行适当的调整，以补偿板材在无压边多点成形过程中受到的回弹影响，得到精确的成形件. 目前，减小回弹的方法主要有两种：一是通过减小成形后的回弹量来保证零件的精度，但此法受材料成形性能和工艺条件的限制；二是不改变回弹量，通过对模具型面的补偿，使其在回弹后获得预期的形状. 补偿法适应性广、成本低，但补偿量的精确计算仍是一个难题. 针对回弹补偿的计算问题，国内外学者做了大量的研究工作[2-7]，文献[5]采用静力隐式算法模拟了板材多点成形的回弹；文献[6]用理论模型和有限元分析探讨了影响板料回弹量的主要因素和提高回弹量预测精度的途径；文献[7]采用显-隐式算法对无压边多点成形中典型曲面的回弹做了数值分析. 本文采用显－隐式算法在ANSYS软件中数值模拟柱面件的回弹，并根据回弹分析的结果，提出一种新的回弹补偿方法，采用该方法对多点成形压力机基本体群的成形面进行补偿，研究板材厚度不同的柱面件的回弹控制.

1 基于回弹数值计算的基本体群成形面的修正方法

1.1 基本体群成形面的修正方法

柱面是一种二维曲面，曲面形状可由端面曲线扫描生成，故可以用端面曲线形状表示整个曲面. 本文利用有限元数值分析的基本思想，将连续的物体离散为有限个单元，提出一种通过修正基本体群成形面以补偿柱面件成形过程中回弹影响的新方法. 具体步骤如下：

1）采用ANSYS有限元软件进行柱面件的多点成形及回弹过程的数值模拟.

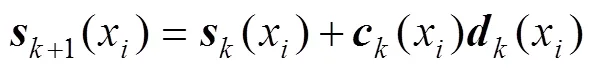
图1 基本体群成形面的修正方法

并检查成形件是否满足成形精度要求，若（为某一给定精度）则满足成形精度要求，得到最终基本体群成形面；否则，基本体群成形面需要进行再次修正，循环以上步骤，直到满足为止，具体修正步骤如图2所示.

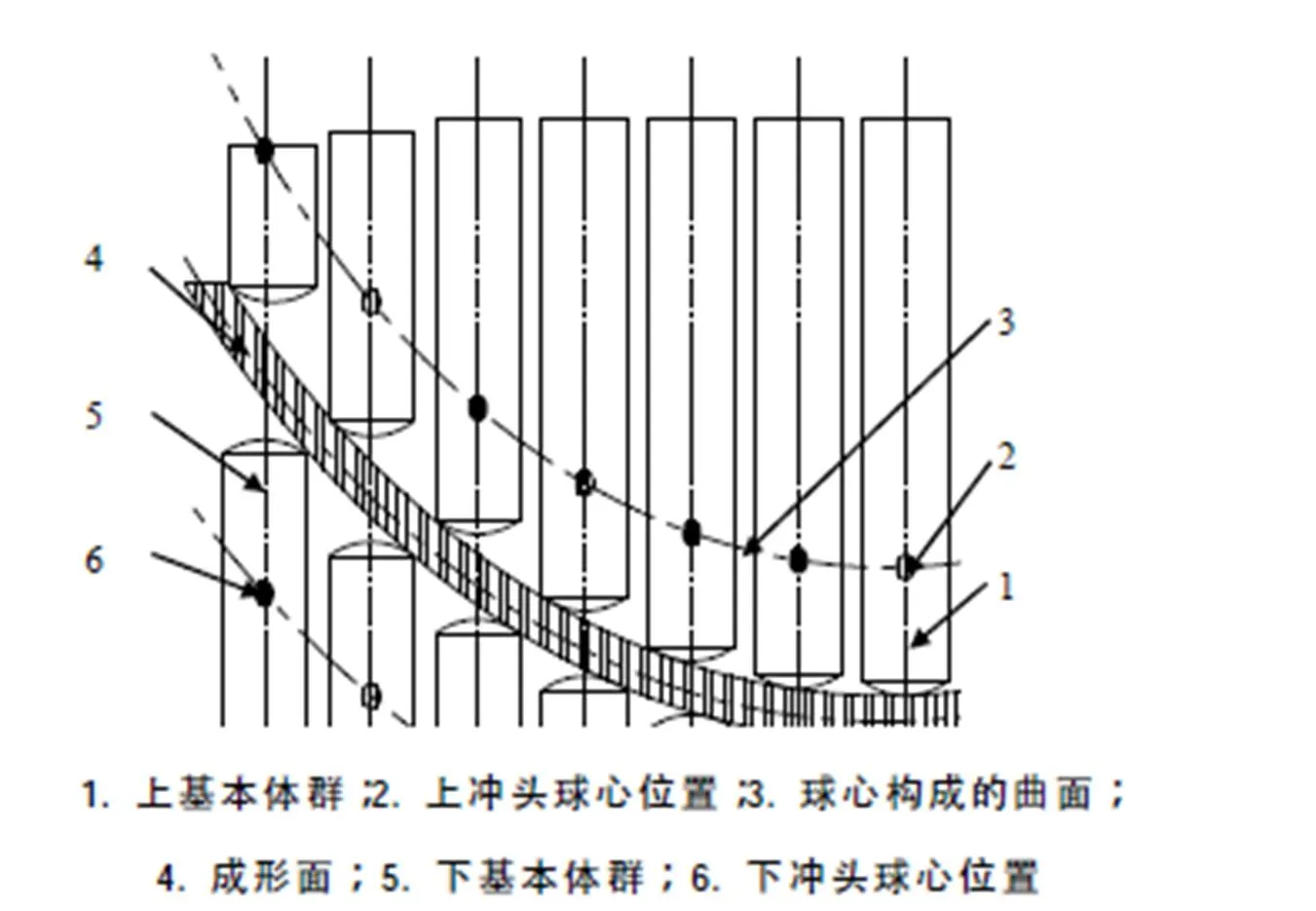
图3 基本体群和成形面的模型图

1.2 基本体群形状的调整

2 应用实例

材料选08Al，弹性模量200 GPa，泊松比0.3，硬化指数0.201，硬化系数537 MPa，屈服应力128 MPa. 板材和基本体单元模型均采用BWC壳单元，由于板材几何形状、约束条件等具有对称性，故只对1/4模型进行分析，其中板材分成4 764个单元，每个基本体分成38个单元，有限元模型如图4所示. 根据目标曲面直接建立基本体群成形面的不同板厚圆柱面成形件回弹后的端面轮廓线如图5所示. ]

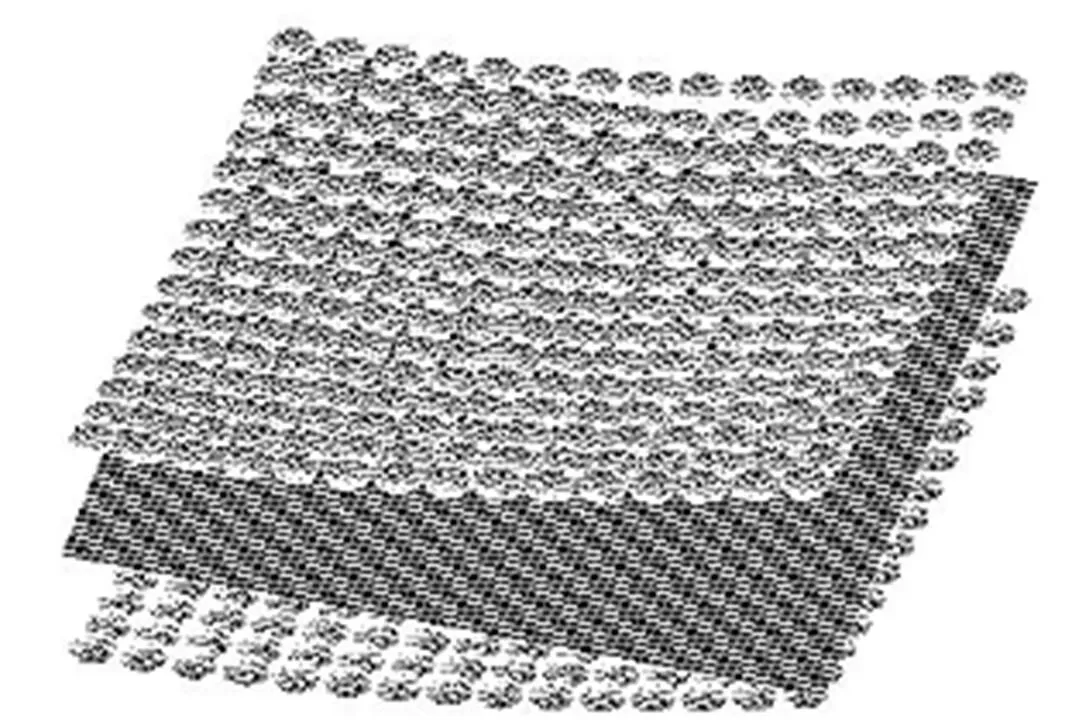
图4 数值模拟的有限元模型（1/4部分）

图5 不同板厚未修正成形面的成形件的端面轮廓线

图6 成形面修正前后圆柱面成形件的端面轮廓线比较

表1 柱面成形件回弹修正过程的总误差 m

3 结束语

本文研究了基于回弹数值计算的典型曲面—柱面件无压边多点成形基本体群成形面的修正方法，并将其应用于实例说明：根据回弹数值分析结果，优化多点成形技术基本体群离散曲面形状可有效补偿板材成形过程中回弹的影响，实现板材的一次精确成形，提高产品的成形精度；回弹补偿量随着板材厚度的增大而减小，当板厚为2.0 mm时，仅需要经过2次修正，形状误差即为0.013 m，因此，在实际生产中如果条件允许，可以选用厚度稍大的板材来控制和减小回弹. 此外，多点成形技术具有整体模具成形不可比拟的优势，对实际工程应用有一定的参考价值和意义.

[1] CAI Zhongyi, LI Mingzhe. Optimum path forming technique for sheet metal and its realization in multi-point forming[J]. J Mater Process Technol, 2001, 110(2): 136-141.

[2] FINN M J, GALBRAITH P C, WU L, et al. Use of a coupled explicit-iImplicit solver for calculating springback in automotive body panels[J]. Journal of material Processing Technology, 1995, 50(1): 395-409.

[3] PAPELEUX L, PONTHOT J P. Finite element simulation of springback in sheet metal forming[J]. Journal of Material Processing Technology, 2002, 125/126: 785-791.

[4] ESAT V, DARENDELILER H, MUSTAFA I G. Finite element analysis of springbak in bending of aluminium sheet[J]. Materials and Desigen, 2002, 23(2): 223-229.

[5] 蔡中义，李明哲，李湘吉. 板材成形回弹数值分析的静力隐式方法[J]. 中国机械工程，2002, 13(17): 458-463.

[6] 张冬娟. 板料冲压成形回弹理论及有限元数值模拟研究[D]. 上海：上海交通大学，2006.

[7] 陈喜娣，蔡中义，李明哲. 板材无压边多点成形中回弹的数值模拟[J]. 塑性工程学报，2003, 10(5): 9-13.

[8] 陈喜娣. 板材多点成形的起皱和回弹数值分析[D]. 长春：吉林大学，2004.

[9] 徐涛. 数值计算方法[M]. 长春：吉林科学技术出版社，1998.

[责任编辑：孙建平]

The Modification and Rebound Control of the Multi-point Forming Cylindrical Surface

CHENXi-di

This paper, based on the results of numerical simulation of rebounds, discusses one new method to modify the elements group’s forming surface in order to compensate for the rebound effect of the cylindrical surface with different thickness in multi-point forming of sheet metal. The results show that, according to the last amendment of the shaped surface, the shape of elements group of the target surface formed in multi-point forming can be adjusted to realize the precise sheet forming while effectively compensating for the rebound effect.

multi-point forming; cylindrical surface; numerical simulation; rebound control

1006-7302（2010）03-0005-37

TG301

A

2010-03-20

陈喜娣（1978—），女，江西新余人，讲师，博士研究生，主要从事金属板材的有限元数值模拟，E-mail: yunqibuzai@yeah.net.