一种基于球坐标的角速率耦合跟踪方法

梁 燊，徐国亮，张 逊

（中国船舶重工集团公司江苏自动化研究所，江苏 连云港 222006）

雷达、光电、陀螺等多种传感器在对机动目标跟踪的过程中，能够获取大量的量测信息，其中包括位置量测信息，也包括速度量测信息。如何对这些信息进行有效地处理和整合，建立合理的目标运动模型，就成为了机动目标跟踪研究的重要课题。利用量测信息对目标状态进行估计，既要做到尽可能地提高状态估计的精度，又要尽量缩短状态估计时间。现有的目标跟踪模型多是针对目标的位置信息进行处理[1-2]，而目标的速度量测信息则没有得到充分的利用。Fitzgerald[3]在滤波过程中加入速度量测信息，分析了速度量测量对滤波的增益和跟踪精度的影响，在同时具备速度量测信息和位置量测信息的条件下，对目标位置的估计精度最高可以提高一个数量级。可见，研究含速度量测信息的目标运动模型具有重要的意义。有学者[4,5]提出加入径向速度信息的模型，跟踪精度有了很大的提高，但模型中均不包括角速度量测信息。Zhu xinguo[6]提出了基于径向距离R的三维、角度q,ε的二维解耦运动模型，能够很好地处理目标的机动性。Pearson和Edwin.B.Stear[7]提出了基于高低误差角和方位误差角的三通道耦合模型，虽然调整了滤波增益以缩短反应时间，但用时仍然较长。本文充分利用径向速度R˙、角速率ω量测值，提出一种新的基于径向距离R，高低角ε、方位角q的三通道球坐标系角速率耦合跟踪模型，提高了状态估计的精度，有效缩短了反应时间。

1 坐标系及问题描述

瞄准线坐标系 O XaYaZa。原点O是跟踪旋转轴与俯仰轴的交点，OXa轴为跟踪器俯仰轴，OYa为跟踪器瞄准线，OZa垂直于 O XaYa的方向，轴OXa、轴OYa和OZa组成右手直角坐标系。如图1，Δq、Δε为方向角和高低角跟踪偏差。设ω为瞄准线坐标系旋转角速度。

图1 瞄准线坐标系与跟踪误差角

东北天坐标系OXYZ。原点位于舰艇中心，OX平行于水平面指向正东，OY轴平行于水平面指向正北，OZ轴垂直平面OXY，铅垂向上为正。

当跟踪偏差 Δ q ＝ Δε ＝ 0，则认为瞄准线坐标系与视线坐标系重合。东北天坐标系与视线坐标系的示意图如图2。

为了使问题简化和研究方便，文中所有模型均在跟踪偏差 Δ q ＝ Δε ＝ 0的假设下建立的。对目标状态的估计，要建立合适的目标运动模型，并选用合理的滤波方法。目标运动模型一般具有如下形式：

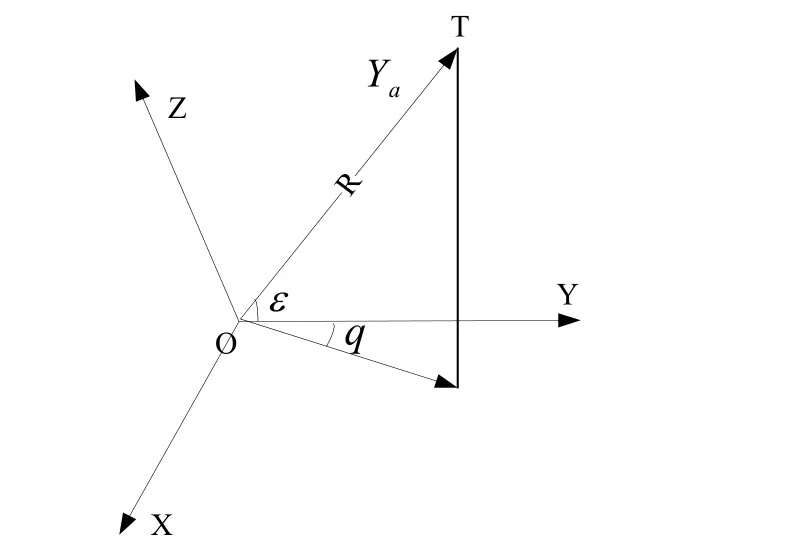
图2 东北天坐标系和视线坐标系

其中X(k)为目标在第k时刻的状态向量，Φ(k)为状态转移矩阵，W(k)为系统的噪声矩阵，

Z ( k)为k时刻的观测向量，H(k)为观测矩阵。V ( k)为 观测噪 声 ，且有 E[V(k )]＝0，E[V(k)V(k)T]＝ R(k)。

对目标运动状态的估计，要在目标运动模型的基础上进行滤波，一般多采用Kalman[8]滤波方法。

实现目标跟踪和预测的关键在于如何从带有噪声的观测量中提出有用的目标状态信息，多数目标跟踪算法是基于目标运动建模技术的。目标运动建模是机动目标跟踪中的核心问题之一。一般所建立的机动目标模型既要符合机动实际，又要便于数学处理。同样对于既具有径向速度R˙，又具有角速度ω量测值的目标运动问题，如何充分利用这些量测信息，建立合适的目标运动模型，就成为问题研究的关键。

2 传统方法

2.1 不含角速度量测的目标运动模型

假设径向距离R在采样时间间隔T内，满足匀加速运动条件，角度q、ε在采样时间间隔T内满足匀速运动条件。可知距离通道R的离散运动模型：

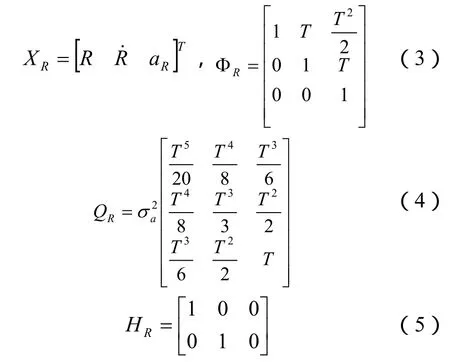
由于方位角q和高低角ε所建立模型相同，这里仅以q为例，给出方程：

系统噪声协方差矩阵为

这里 ωza,ωxa分别为方位角q的角速率在OZa方向上的分量、高低角ε的角速率在OXa方向上的分量。为系统的噪声方差。

2.2 含角速度量测的目标运动模型

这里距离通道R所采用的模型仍然是匀加速模型，它的离散时间模型与不含角速率量测的目标运动模型相同。即状态向量和状态转移矩阵为式（3），系统噪声矩阵为式（4），观测矩阵为式（5）。

对于角度通道q、ε，假设角度的变换在采样时间间隔T内满足匀加速运动模型。这里仅以q为例，给出它的离散时间模型：

观测矩阵：

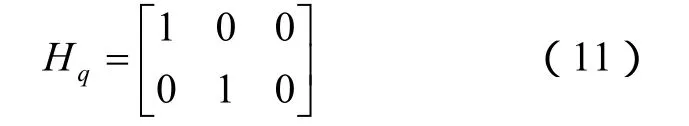
这里ωza为方位角q的角速率在OZa方向上的分量。aza分别为q的角加速度在OZa方向上的分量。为系统的噪声方差。

3 球坐标角速率耦合跟踪方法

在瞄准线坐标系下，目标的坐标为：

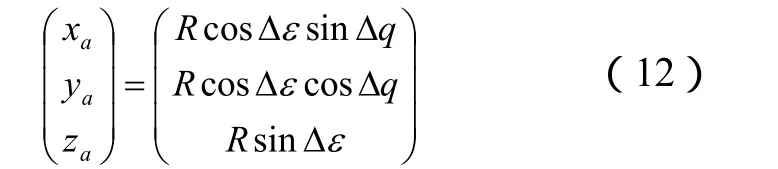
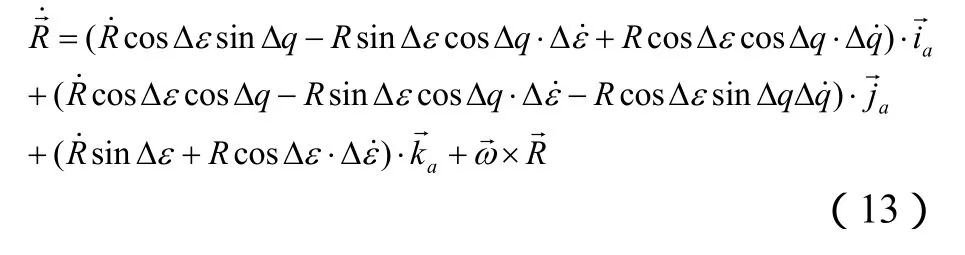
若跟踪偏差 Δ q ＝ Δε ＝ 0，瞄准线坐标系与视线坐标系重合，则可得：

等式（15）可以写为如下形式：

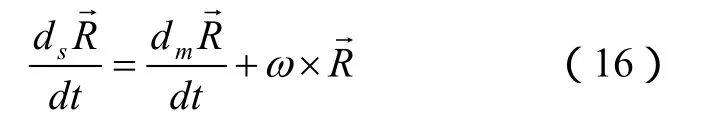
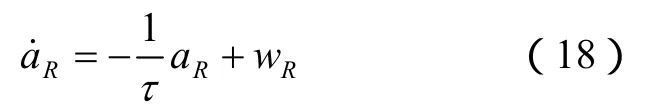
对于R，有运动学方程：

对式（19）离散化，可以得到：

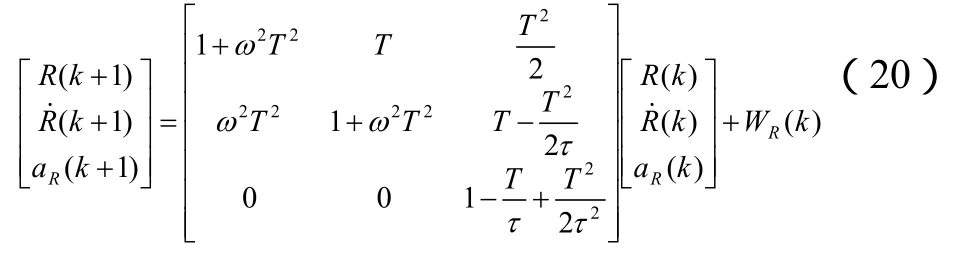
QR为XR的系统噪声矩阵，HR为观测矩阵。τ为OY方向上的机动时间常数。

对于角度q，ε，同样假设在采样时间间隔T内，它们的变化满足匀加速条件，则它们运动模型同样可以写为式（9）、（10）、（11）。

对于含径向速度和角速度的耦合模型，滤波过程首先从角度滤波开始，将得出的最优估计的ωˆza和ωˆxa代入距离通道R的方程中，通过距离通道的自身滤波来求得R的最优估计值，这样就完成了一次滤波过程。滤波过程示意图如下：

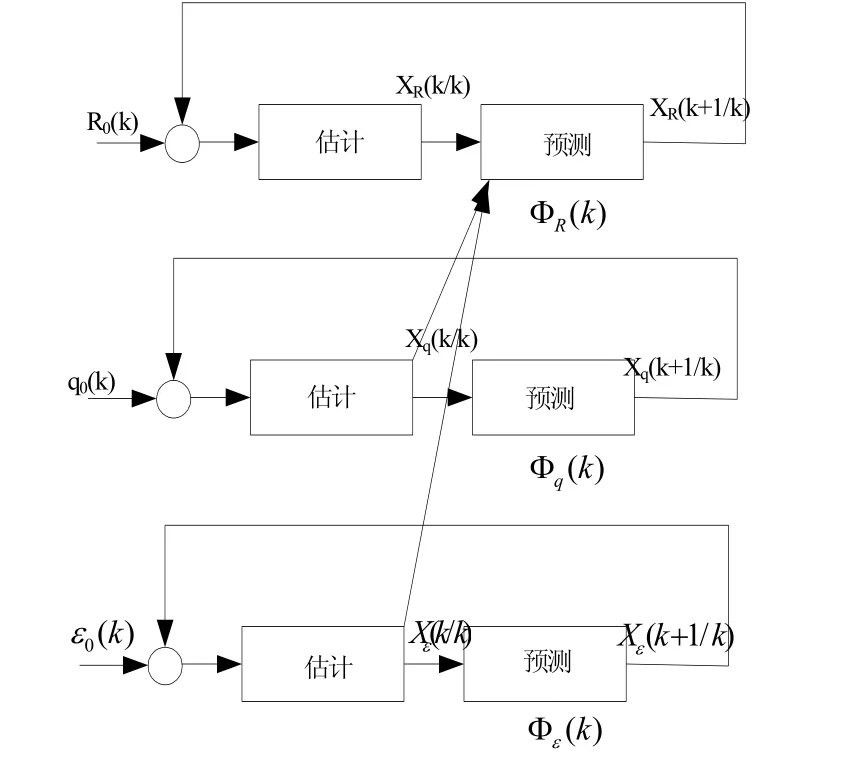
图3 滤波过程

4 仿真计算

图4 目标运动示意图

航路一：假设目标距观测点的初始距离为6000m，目标距地高度为 50m，航路捷径为 300m，采样周期T＝0.02s 。目标运动时间为20s。

观测误差的标准差 σR＝10m ，σq＝σε＝1mrad，径向速度的标准差＝5m /s ，角速度的标准差

仿真均采用kalman滤波方法。进行Monte Carlo仿真300次。为简单起见，仅给出了方位角通道滤波均方根和径向距离的误差均方根曲线图如图5、图6。

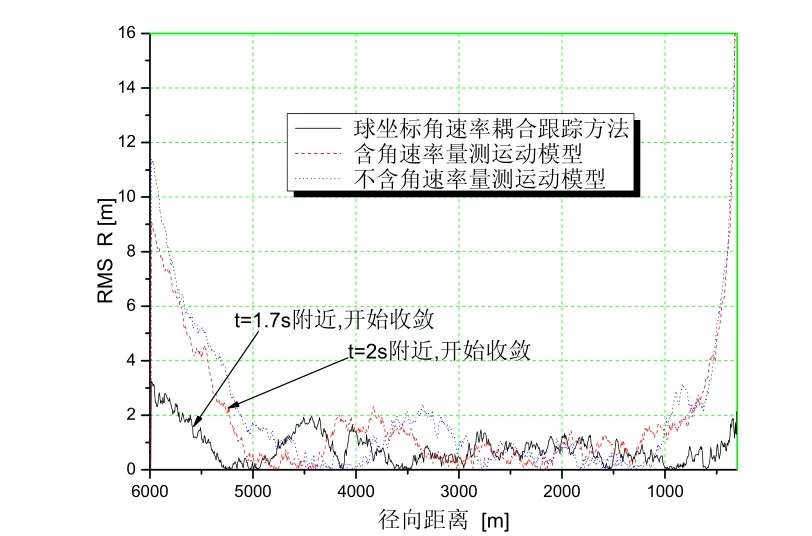
图5 R的误差均方根

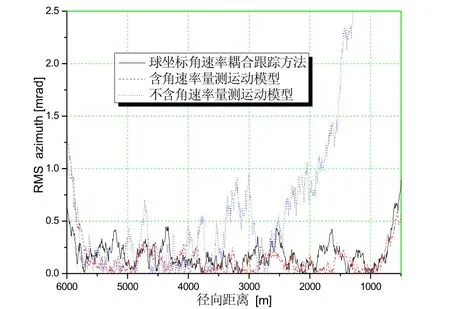
图6 方位角q的误差均方根

通过仿真图形，可以得出：使用了角速率耦合跟踪方法对径向距离R进行滤波，能够较快的收敛，并且误差均方根较小。在目标与观测点最接近点，仍然能够保持较小的误差。对于角度的滤波，我们可以看到使用了角速率量测值的耦合模型，目标最接近观测点时角度估计仍然保持较小的误差均方值。

为了比较在不同航路下球坐标角速率耦合跟踪方法的效果，设计了另外一条航路：航路捷径为100m，其他条件与航路一相同。同样进行Monte Carlo仿真300次，二者的径向距离和角度误差均方根对比如图7、图8：

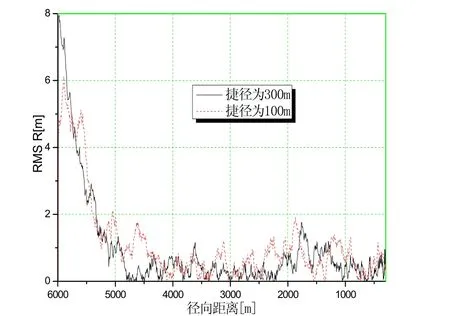
图7 航路一与航路二的径向距离误差均方根对比图

通过仿真图形，可以得出：在所选的两条航路上，使用球坐标角速率耦合跟踪方法对径向距离R进行滤波，从滤波稳定开始至滤波结束，滤波的误差均方根相差不多。在滤波结束点附近，捷径越小的航路的角度滤波收敛性越好。

图8 航路一与航路二的方位角误差均方根对比图

5 结束语

本文分析了球坐标系下的跟踪滤波过程，提出了基于球坐标的角速率耦合跟踪方法。在考虑了瞄准线坐标系绕惯性坐标系旋转所产生的Coriolis加速度的情况下，建立了径向距离R的运动模型。本文将基于球坐标的角速率耦合跟踪方法与不含角速率量测和含角速率量测值的两种运动模型做了对比。仿真结果显示，含角速率量测的运动模型和角速率耦合跟踪方法的跟踪精度明显优于不含角速率量测信息的运动模型；而与含角速率量测的模型相比，应用基于球坐标的角速率耦合跟踪方法，能够使径向距离较快地收敛，并且在整个滤波过程中保持较好的收敛性。

[1]X. Rong. Li, Vesselin . P. Jilkovt. A Survey of Maneuvering Target Tracking: Dynamic Models[J]. IEEE Transactions on aerospace and electronic systems.Oct,2003: 1333-1364.

[2]H.Thou, K. S. P. Kumar. A "Current" Statistical Model and Adaptive Algorithm for Estimating Maneuvering Targets[J].AIAA Journal of Guidance, Sept.-Oct. 1984,7(5):596-602.

[3]Robert. J, Fitzgerald. Simple Tracking Filters: Position and Velocity Measurements[J]. IEEE Transactions on aerospace and electronic systems. Sept.1982,AES-18,NO.5:531-537.

[4]张怀根,张林让,吴顺君.利用径向速度观测值提高目标跟踪性能[J]. 西安电子科技大学学报(自然科学版),2005, 32(5):667-670.

[5]S. Zollo, B. Ristic. on polar versus Cartesian coordinates for target tracking[C]. Fifth International Symposium on Signal Processing and its Applications, ISSPA,1999:499-502.

[6]Zhu xinguo, Hong Jie, Cui wei. Study on Radar Data processing Algorithm with Improved Kalman Filter[C].ICIEA 2009: 3826-3829.

[7]J. B. Pearson, E. B. Stear. Kalman Filter Applications In Airborne Radar Tracking[J]. IEEE Transactions on aerospace and electronic systems.May.1974,AES-10(3):319-329.

[8]R. E. Kalman. A new approach to linear filtering and prediction problems[J]. Trans. ASME, J.Basic. Engrg,1960,82(2):34-45.

[9]王洪兰.陀螺理论及在工程测量中的应用[M].北京：国防工业出版社，1985:47-57.