海上不明空情威胁评估模型研究

陈晓曦，姚景顺，沈振华，侯玉梅

（1.海军大连舰艇学院，辽宁 大连 116018；2.德州学院，山东 德州 253023）

1 概述

海军在执行非战争军事任务时如索马里护航、奥运海上安保等任务时，常遇到突发性的不明空情，其最突出的特点是敌我属性和意图均无法明确；并且空情数据来源于各种传感器或数据链，数据本身具有不确定性；因此如何处理空情信息的不确定是评估不明空情威胁程度的关键所在，也是海上编队完成任务及保障自身安全的一个重要前提。

目前，基于知识表示和推理的方法是当前国内外威胁评估领域的主要建模方法，有专家系统、黑板系统、逻辑模板匹配和贝叶斯网络等算法。贝叶斯网络算法应用于有条件的依赖和多种控制因素的决策；相对于其它算法，它以网络图形的方式描述人类的推理模式，量化推理过程，收敛性和实时性较好，能反映推理过程的连续性和累积性，已广泛运用于火力威胁评估[1]，态势估计[2]、目标识别[3]等领域。本文将运用此算法来处理信息的不确定性，对不明空情的威胁评估展开研究。

2 贝叶斯网络

2.1 贝叶斯网络概述[4]

贝叶斯网络是用一个＜G,P＞二元组表示，G表示一个由节点和指向节点的边组成的有向无环图（图1）。其中节点表示随机变量，是对事件、状态等实体特征的描述；有向边表示变量之间的依赖关系。这种依赖关系通过一组条件概率P表示。每个节点的条件概率可用P=(X|m(X))表示，其含义是节点X相对于父节点的条件概率。

图1 贝叶斯网络示意图

2.2 贝叶斯网络推理

第一步：更新自身的后验概率

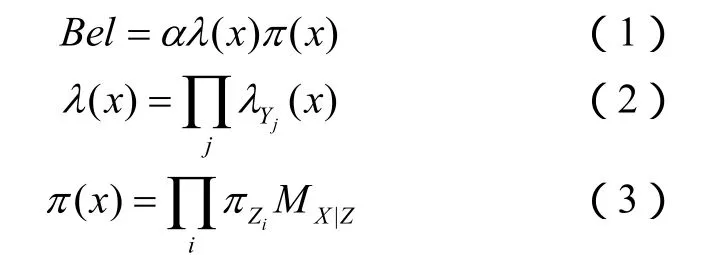
第二步：自底向上更新

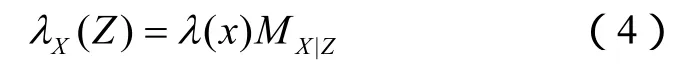
第三步：自顶向下更新

3 模型建立

3.1 确定威胁因子

如何从获取的信息中分析并提取出与不明空情威胁程度相关的威胁因子（Threaten Genes），从而确定网络结构中的节点是建立模型的基础。美国海军专家Liebhaber和Smith在2000年对海上空情威胁因子有过有效的研究[6]。考虑非战争条件下的空情特点，在评估不明空情威胁时，可主要考虑以下因子：

● 飞行航线 (Flight Air-lane)

● IFF信号回应（IFF Response）

● 起飞机场 (Original Airport)

● 武器使用迹象(Weapons Apparent)

● 告警信号回应(Warning Response)

● 空情通报（Intelligence Report）

● 空情数量（Number）

● 速度（Speed）

● 飞行高度（Flight Altitude）

● 航路勾径（CAP）

● 信号辐射类型（Electronic Signal type)

● 距离（Range）

● 雷达回波观察（Echo Observation）

● 高度变化（Altitude Change）

苔藓和地衣下面的冻土层好比是北极的一座天然冰箱，寒冷的气候冷冻了土壤，也顺带冷冻了土壤里的各种有机物。然而，由于人类活动导致的全球气候变暖，使得冻土和周围的海冰逐渐融化。土壤中的微生物被释放出来，参与化学反应，向大气释放二氧化碳、甲烷等气体，而这些气体反过来又加速了全球气候的变暖。也许你会说，天气变暖，驯鹿迁徙的路就不那么难走了，可出人意料的是，天气变暖会让驯鹿饿肚子！

确定各节点后，需分析各节点之间的关系。这些节点在网络中可能位于同一层次，也可能位于不同层次而存在依赖关系。根据节点条件依赖关系，建立图2所示的贝叶斯网络。影响不明空情威胁等级的直接因子共7个，位于网络第二层；次因子5个，位于第三层。

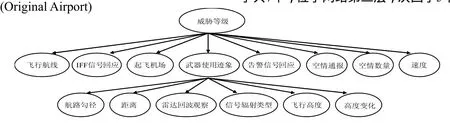
图2 不明空情威胁评估网络

3.2 因子状态确定

威胁等级（TL）：按照惯例，可把威胁程度分成三个等级，即 TL1=“低”，TL2=“中”，TL3=“高”；

飞行航路 (FL)：民用飞机的飞行航线是有一定宽度的空域，该空域以连接各导航设施的直线为中心线，规定有上限和下限高度和宽度。按照国际民用航空公约的规定，航路的基本宽度为航路中心线两侧各 4海里（7.4公里）[7]。当某一空情明显偏离航路中心线 4海里以上，可被视成军用飞机或意图不明的民用飞机。因此，该因子状态可取值为 FL1=“位于民航航线”，FL2=“偏离民航航线4海里以上”；

IFF信号回应(IFF)：民航机与军用机均安装了应答机以利于识别。根据信号发射频率和代码特点，应答机有模式1、模式2、模式3/A、模式4，模式5，模式B、模式C、模式D和S模式。其中民用模式有模式3/A（军民合用），模式C和S模式[8]。因此，该因子状态可取值为IFF1=“民用应答信号”，IFF2=“军用应答信号”，IFF3=“无应答信号”；

起飞机场 (OA)：在近海，根据发现空情最初点、航向及比对民用航线后，可判定起飞机场类型。因此，该因子状态可取值为OA1=“民用机场”，OA2=“军民两用”，OA3=“军用机场”，OA4=“不明机场”；

武器使用迹象（WA）：导弹是主要的空对舰攻击武器；炸弹投掷是飞机对海攻击传统方式；自杀性袭击是执行非战争任务时面临的主要威胁之一。无论不明空情采取何种攻击方式，都会作出一系列相应的空中动作或辐射一定类型电磁信号。根据这些特征，能判断出目标攻击的方式。因此，该因子状态可取值为WA1=“导弹”，WA2=“炸弹”，WA3=“自杀式袭击”，WA4=“无”；

告警信号回应（WR）：不明空情进入对空告警空间后，海上编队会在特定频道对其发出无线电告警信号，迫使其采取一定的措施远离本方以消除威胁。因此，该因子状态可取值为WR1=“明确回复”，WR2=“含糊回复”，WR3=“无回复”；

空情通报 (IR)：除依靠本舰对空探测器材获取空情外，还可通过数据链等其它通信方式获取来自友方的空情信息。因此，该因子状态可取值为IR1=“空情通报无威胁”，IR2=“空情通报不明”，IR3=“空情通报有威胁”；

空情数量（Num）：在同一飞行航路上，同一时刻民用机出现的数量为单架。双机以上组成的空中编队一般为军用飞机。因此，该威胁因子状态可取值为：Num1=“单架”，Num2=“双架以上”；

飞行高度（FA）：飞机在发射空舰导弹时，其飞行高度必需满足导弹发射要求，高度通常在800-3000m之间；飞机实施炸弹投掷及自杀性袭击时，其飞行高度一般在800m以下。因此该因子状态可取值为FA1=“3000m以上”，FA2=“800-3000m”，FA3=“800m 以下”；

高度变化（AC）：飞机采取不同的攻击手段时，其高度变化也不同。如为保障炸弹投掷的精度，飞机的飞行高度会保持不变；飞机实施自杀式袭击时，会高速俯冲；在实施导弹攻击战术时，飞机的高度一般会经过爬升、保持再下降的过程。因此，该因子状态可取值为 AC1=“俯冲”，AC2=“平飞”，AC3=“爬升”；

航路勾径（CAP）：在发射传统直向攻击导弹时，飞机须不断改变航向以减小航路勾径。随着可规划航路导弹的运用，航路勾径对导弹发射的限制越来越小。而飞机在实施炸弹轰炸及自杀性袭击时，其航路勾径几乎为零。因此，该因子状态可取值为CAP1=“3km以内”，CAP2=“3－10km”，CAP3=“10km 以上”；

电子信号辐射（ES）：实施导弹攻击前，飞机一般要经过机载雷达搜索发现目标、锁定跟踪目标过程，期间舰载电子战系统会截获机载雷达辐射信号。因此，该因子状态可取值为 ES1=“截获非军用机载雷达信号”，ES2=“截获军用雷达搜索信号”，ES3=“截获军用雷达锁定信号”， ES4=“未截获任何雷达信号”；

距离（RA）：先进的空舰导弹最大射程可达100Km以上，但拥有此类导弹或制造技术的国家为避免导弹扩散，对其有着严格限制。因此，海上编队面临主要的空舰导弹有效射程一般在 50-100Km，而飞机在实施自杀性袭击及炸弹投掷时，其攻击距离至少在25Km以内。因此，该因子状态取值为RA1=“25Km以内”，RA2=“25－50Km”， RA3=“50－100Km”，RA4=“100Km 以上”；

雷达回波观察（EO）：飞机在发射导弹时，雷达显示器会出现明显的回波分离变化。因此，该因子状态可取值为EO1=“回波无变化”，EO2=“回波分离”。

3.3 条件概率分配

贝叶斯网络模型建立以后，需要确定各节点因子之间的条件概率。条件概率可根据领域专家知识进行确定，也可通过测试大量数据并运用参数学习的方法来确定。本文先根据专家知识初步确定条件概率，并通过利用“Stark”、“Vincennes”案例及海军演练等样本数据反复调试条件参数，尽可能消除专家知识的主观性，以提高评估模型的可信度。条件参数调试的结果见表1-4。

表1 条件矩阵

表2 条件矩阵

表3 条件矩阵

表4 条件矩阵

4 模型仿真

4.1 案例概述[9]

两伊战争进入“油轮战”后，美中东舰队为中立国提供海上石油运输安全保障。护航期间，美军舰“Stark”号在公海巡逻时发现一不明空情，因其作战人员对该不明空情的威胁评估产生错误，被伊拉克战斗机发射的两枚导弹击中，造成37名官兵牺牲。“Stark”事件是国际海军判断不明空情威胁程度的一个典型案例。根据美国军方事件调查报告，对该案例进行仿真，以验证模型的有效性。

4.2 仿真验证

2058，“Stark”号接到上级通报，获取如下先验信息：从伊拉克军用机场起飞的一不明空情，航向155°，航速530km/h，高度900m，距离70.2海里，航路勾径17.7km，正逐渐接近“Stark”号。网络节点Num、FA、CAP、RA、OA、IR、SP、CA、FL获取信息，由2.2节的推理算法，采用 MATLAB语言编制贝叶斯网络算法程序，获取如表5所示的仿真结果。

2102，舰载雷达探测到不明空情距Stark号约48.4海里，航路勾径约4海里；舰载电子战系统截获军用机载雷达搜索信号。网络节点ES、CAP、RA得到新信息，整个网络更新结果如表6所示。

2105，伊机航向小调整后，航路勾径几乎为零；此时对不明空情威胁程度的评估结果如表7所示。

2106，伊机航向157°，高度900m，速度580km/h，距离Stark号约27海里；此时对不明空情威胁程度的评估结果如表8所示

2108，不明空情距Stark号约15.5海里；舰载电子战系统截获军用雷达锁定信号后；Stark号对其发出的无线电告警信号未收到任何回复；此时对不明空情威胁程度的评估结果如表9所示。

表5 2058时威胁仿真结果

表6 2102时威胁仿真结果

表7 2105时威胁仿真结果

表8 2106时威胁仿真结果

4.3 结果分析

由表 5知，2058时，Bel(WA)概率分布为(0.1352,0.0014,0.0,0.8633)，其中目标不使用武器的迹象概率最高；Bel(TL)低、中、高威胁等级概率分布为（0.027,0.7379 ,0.235)，根据最大概率法可评定目标的威胁程度为中。

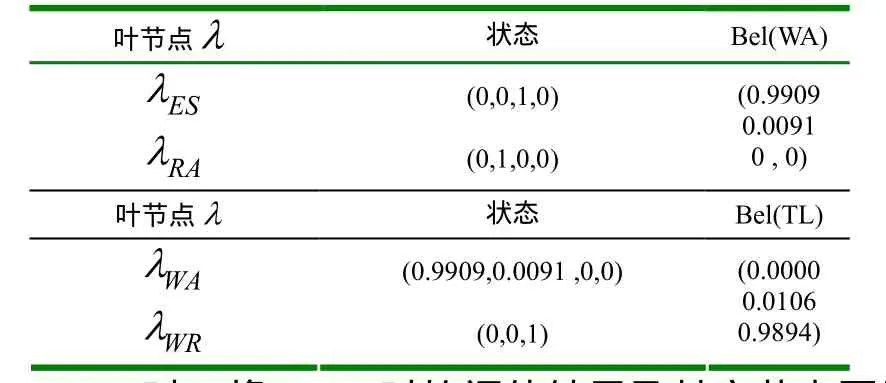
表9 2108时威胁仿真结果

2102时，将2058时的评估结果及其它节点因子的更新信息作为2102时输入参数。结果显示空情使用导弹的迹象概率最高，威胁评估结果更新为(0.0019,0.4171,0.581)。与上一时刻相比，低威胁的概率为零，高威胁的概率明显增大。此时，“Stark”号作战人员应准备采取积极防御措施。

由表7和8知，随着空情航路勾径和距离不断减小，高威胁概率不断增加；2105时，高威胁的概率已明显高于中威胁的概率。

由表9知，2108时，在更新λES和λRA威胁因子信息后，高威胁的概率达到0.99；目标对“Stark”号构成十分严重的安全威胁。从美军解密的事件调查报告知，此刻伊机正向“Stark”号发出第一枚导弹。仿真结果能与美军的调查结果及事件进程相吻合。因此，该评估模型具有很高的可信性。

5 结束语

本文提出了一种基于贝叶斯网络的海上不明空情威肋等级评估模型。该模型具有信息累积及动态实时评估的能力，符合人类专家的评估特点。经过实际案例验证，该模型能够准确地评估海上不明空情的威胁等级；从而能为指挥人员提供辅助决策，对可能发生的攻击提前采取措施以消除空中威胁，从而保障海上编队安全。

[1]税薇,葛艳. 基于贝叶斯网络的火力威胁等级评估算法[J].系统仿真学报,2009,15(8):4625.

[2]张雪梅,高晓光. 贝叶斯网络用于作战态势评估[J].火力与指挥控制,2008,33(10):30.

[3]郭小宾,王壮,胡卫东. 基于贝叶斯网络的目标融合识别方法研究[J].系统仿真学报,2005,17(11):2713

[4]张连文,郭海鹏. 贝叶斯网引论[M].北京:科学出版社,2006.

[5]Neil M,Fenton N,Nielsen L. Building large-scale Bayesian networks[J].The Knowledge Engineering Review (S0269-8889),2000,15(3):257-284.

[6]Liebhaber, M. J., Smith, P. Naval Air Defense Threat Assessment: Cognitive Factors and Model,[D]Command and Control Research and Technology Symposium,Monterey, CA, June 2000.