水平轴风力机叶片翼型流场的数值模拟

闫海津,李 佳,胡丹梅

(上海电力学院能源与环境工程学院,上海200090)

水平轴风力机运行时,如果翼型来流的攻角较大,绕翼型的流动边界层就会严重分离,因此准确获得翼型的气动特性对于风力机叶片设计非常重要,但是这种复杂的分离流动现象采用试验的方法测量非常困难,而且大量的试验将使翼型的设计周期延长和成本增加。采用CFD计算流体力学数值模拟替代试验测定工作确定翼型的气动特性,可以缩短设计周期和降低设计成本,已经在实际工程中得到了广泛的应用。NACA634系列翼型是一种总体性能表现良好的翼型,在各种水平轴风力机上得到了广泛的应用,本文将采用CFD软件FLUENT对该系列翼型中的NACA63425进行数值模拟[2-4],得出翼型在不同攻角下的压力分布、升力系数、阻力系数及升阻比,分析翼型的分离流动情况。

1 风力机叶片的数值模拟

1.1 基本方程

风力机叶片的运转速度不大,翼型的绕流可以看作不可压缩流动。数值计算模型采用二维连续性方程和二维不可压缩N-S方程[3]。

二维连续性方程:

二维不可压缩N-S方程:

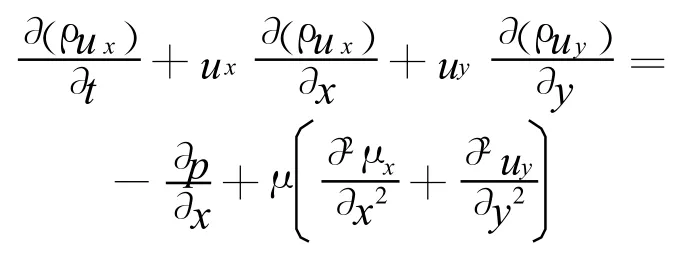
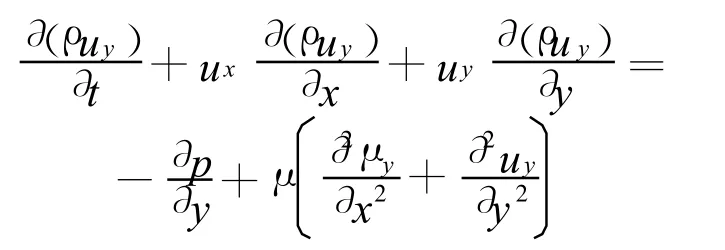
式中:ρ为空气密度;μ为空气的粘性系数。

1.2 网格划分

由于所采用翼型的几何形状并不十分复杂,考虑到数值求解效率等因素,本文采用了C型网格。为了减少计算域外的边界对计算过程的影响,外边界长度分别取翼型弦长和最大厚度10倍左右的距离。为了能够得出更加准确的结果,网格在翼型表面采取了网格局部加密方法[1],网格总数达6万多,其中翼型表面分布节点160个。网格分布见图1。

图1 网格分布图

1.3 定解条件和边界条件

采用分离式求解器进行求解,隐式算法。模拟计算假定流场中只存在空气单相流动,不考虑风沙、水滴等多相流的情况;空气密度和空气动力粘度依据模型提供的常规值并且保持为常数。因为气流密度小计算中可以不考虑重力的影响。在求解过程中可以假定所有过程都是绝热过程,即不考虑热传导与太阳辐射。本文的模拟选用RNG k-ε两方程湍流模型,该湍流模型能够反映各向异性和平均涡量对流动的影响,其中的湍流常数直接由重整化群理论导出并且在模型中通过一个修正项记入了平均应变率对湍流耗散率的影响,具有较高的精度和可信度[2]。方程中压力--速度耦合采用SIMPLE算法即求解压力耦合方程组的半隐式方法,这也是目前工程上应用最为广泛的流场计算方法,主要用于求解不可压缩流场的数值方法,这种方法的核心是采用“猜测-修正”的过程,在交错网格的基础上来计算压力场,从而达到求解动量方程(Navier-Stokes方程)的目的[2]。方程中的动量、湍流动能均采用二阶迎风格式处理。

边界条件包括进出口边界和壁面边界:设定进口边界为速度进口边界条件,速度为无穷远处的来流风速;考虑到计算区域相对弦长较大,流动在出口处已经得到了充分的发展,所以选用自由出流为出口边界条件;翼型表面为无滑移固壁边界。

2 计算结果与分析

2.1 升力系数、阻力系数及升阻比

对NACA63425翼型流场在来流攻角为0°至30°范围下的流动情况进行的数值模拟,取来流的速度为风力机在额定工作状态下的风速,12m/s。利用数值计算得到的翼型升力系数、阻力系数和升阻比随来流攻角的变化结果见图2-图4。

图2 升力系数随来流攻角的变化

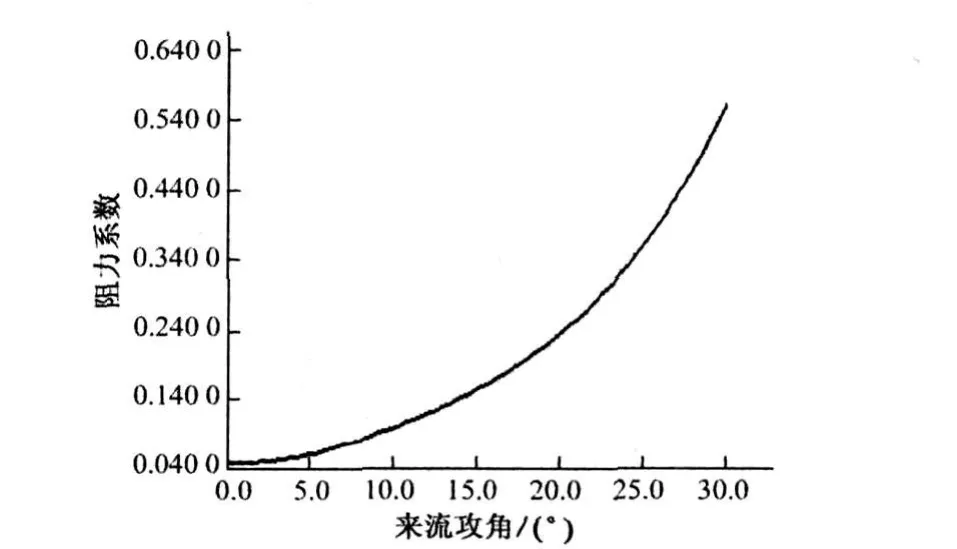
图3 阻力系数随来流攻角的变化

从图中可以看到:当攻角小于12°时,翼型的升力系数和阻力系数都随着攻角的增大而增加;攻角在12°左右时,翼型的升力系数达到最大;当攻角大于12°后,翼型的阻力系数继续增加,但是升力系数开始下降,不过攻角增加到25°后升力系数又开始上升。这是因为随着攻角的增加,气流在翼型表面上的分离加剧,导致尾迹区域形成漩涡,翼型上下面压力差和升力减小,风机进入了失速状态。根据这些模拟计算结果可以看到,翼型NACA63425的失速攻角应该在12°附近。在实际中,风力机叶片一旦出现失速现象,风力机就会产生剧烈振动和运行不稳,为了使风力机在稍大于设计风速时仍能很好的工作,所选取的升力系数应在升力系数最大点的左侧,其值最大不超过0.8～0.9倍的最大值[5]。

图4 升阻比随来流攻角的变化

翼型的升阻比反映了翼型的气动效率,升阻比越高,翼型的气动效率越高。由图4可以看出,在来流攻角为7°左右时翼型的升阻比达到最高,约为l2左右。来流攻角大于7°时升阻比急剧下降,在攻角为30°时翼型的升阻比已经下降到2左右。

2.2 翼型表面的压力分布

不同的攻角翼型表面的压力分布的模拟计算结果见图5-图7。

图5 攻角为 10°时翼型表面的压力分布

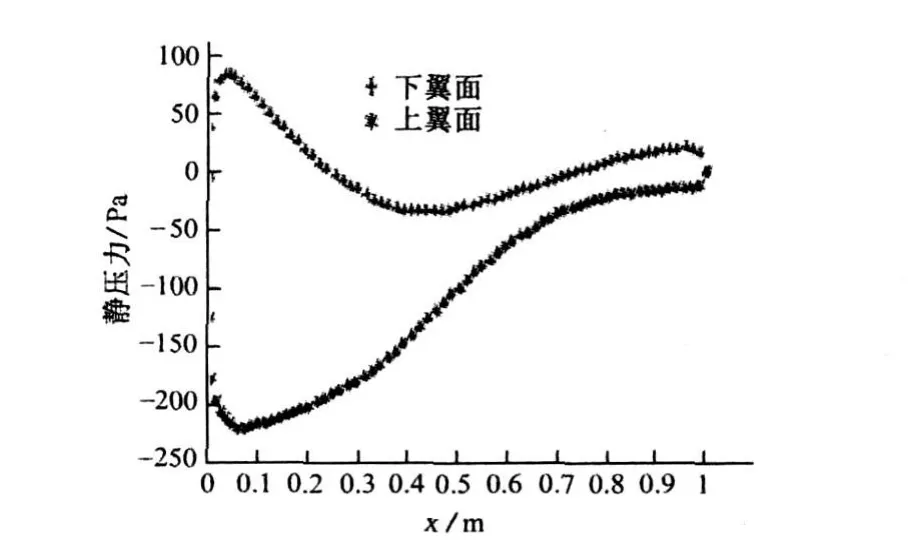
图6 攻角为 14°时翼型表面的压力分布

图7 攻角为18°时翼型表面的压力分布

对比图5,图6和图7可以看出,当来流攻角为10°时翼型上下表面始终具有较大的压差。当来流攻角增大到14°时翼型尾部上下表面的压力差就有所减小了,随着来流攻角的进一步增大,压力差减小的趋势向着翼型的前缘方向发展。对比图6和图7可以看出,当攻角为14°时压差开始减小的位置大概发生在0.6弦长处,当攻角为18°时压差减小的点已经向翼型前缘移动到弦长的0.5处左右了。造成这种现象的主要原因其实也是翼型表面的流动分离随着攻角的增大而加剧,并且有向着翼型前缘方向发展的趋势。

2.3 翼型流场的流线分布

不同攻角时翼型流场的流线分布模拟结果见图8-图10。

图8 攻角为10°时翼型流场的流线分布

图9 攻角为14°时翼型流场的流线分布

图10 攻角为18°时翼型流场的流线分布

由图8可得出,当来流攻角小于10°时,翼型绕流为附着流,未出现漩涡分离的现象;此时的翼型表面压力分布图也呈现出较大的压差,即此时翼型具有较好的气动性能,但当来流攻角增大到14°后,翼型尾部开始出现流动分离形成了漩涡(见图9)。从图10中还可以进一步看出,随着攻角的增大漩涡的范围也进一步的扩大,并向翼型前缘发展[5-7];这也正是翼型升力系数变小,表面压差减小并且减小的趋势向前缘移动的原因。可见,翼型流场的尾迹流动分离是影响翼型气动特性的主要原因。

3 结论

本文利用计算流体软件FLUENT对不同攻角下翼型NACA63425流场进行了数值模拟,得出了翼型在不同攻角下的压力分布、升力系数、阻力系数并计算得出了升阻比。本文还通过模拟结果分析了翼型的分离流动情况,得出了影响翼型气动性能的主要原因,总结了该翼型分离流动随攻角的变化特征,为风力机翼型的气动特性研究提供了参考依据。

[1]Nathan Logsdon.A procedure for numerically analyzing airfoils and wing sections[D].The Faculty of the Department of M echanical&Aerospace Engineering University of Missouri-Columbia,2006.

[2]赵伟国,李仁年,李德顺,等.风力机专用翼型数值模拟中湍流模型的选择[J].西华大学学报,2007(11):61-65.

[3]陈旭,郝辉,田杰,等.水平轴风力机翼型动态失速特性的数值研究[J].太阳能学报,2003(12):735-740.

[4]杨从新,李春辉,巫发明.水平轴风力机专用翼型的数值模拟研究[J].科学技术,2008(9):4994-8994.

[5]M ENG F.CFD investigations with respect to model sensitivity for the non-rotating flow around the NREL Phase VI Blade[R].Delft University Wind Energy Research Institute,2008.

[6]李栋,李孝伟,乔志德.大迎角粘性复杂流场的数值模拟[J].空气动力学学报,2000(6):311-315.

[7]王友进,闫超,周涛.不同厚度翼型动态失速涡运动数值研究[J].北京航空航天大学学报,2006(2):153-157.