列车运行时分力学模型的建立与仿真

颜保凡，郭垂江，廖 勇

(1.湖南铁路科技职业技术学院 运输管理系，湖南 株洲 412000；2.西南交通大学 交通运输学院，四川 成都 610031)

在新否建满铁足路设或计既通有过线能改力造和时列，车需安验全证运线行路的平要纵求断，面但是不具备列车牵引试验的条件，可用列车运行时分计算 (列车牵引计算) 替代，通过仿真获得比较精确的数据。在实践中，列车力学模型对计算结果的影响，不同的专家看法不一。一些专家认为，单质点列车力学模型具有易于建模和良好的数学特性，特别是列车自动计算的算法易于实现，并且对区间运行时分的影响不大。另一些专家认为，单质点列车力学模型不能如实反映列车运行过程中受力的动态变化，计算结果偏差较大，因此提倡多质点列车力学模型。以下对列车运行模拟中的单质点和多质点列车力学模型给出各自的数学模型，通过模拟仿真分析不同模型对列车运行的影响。

1 单质点列车力学模型

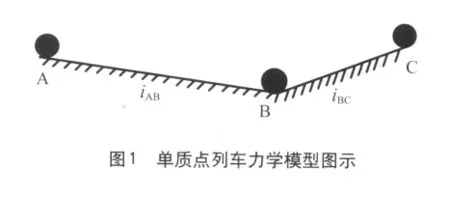
单质点列车力学模型将整列车视为一个刚性的质点，忽略了列车的长度和车辆之间的相互作用力，当列车跨越变坡点 (曲率变化点) 时，列车的附加阻力发生突变。如图1所示，列车进入坡段 AB，自 A 点到坡段末端 B 点列车受到的单位附加阻力均为 iAB。当列车越过变坡点 B 后，列车的单位附加阻力由 iAB突变到 iBC，一直保持到 C 点出坡。简化的单质点列车力学模型偏离了列车真实的纵向力学特性，不能精确地反映列车在运行过程中力学的动态变化。但由于在分析计算过程中其计算量小，易于操作和利于图解等特点，在手工作业和电算初期采用较为广泛。

列车在运行过程中除受到牵引力、基本阻力和制动力外还受到坡段附加阻力、隧道附加阻力和曲线附加阻力。3 种附加阻力可折算成单位加算附加阻力：

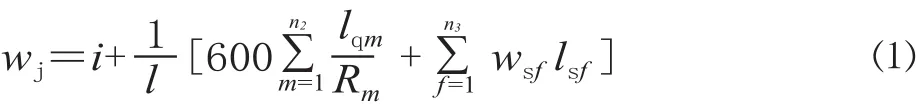
式中：wj为单位加算附加阻力，N/kN；i 为坡段的坡度，‰；l 为坡段的长度，m；Rm为坡段内第 m 个曲线的半径，m；n2为坡段内曲线的数量；lqm为坡段内第 m 个曲线的长度 (未在坡段内的部分长度除外)，m；wsf为坡段内第 f 个隧道的单位附加阻力，N/kN；lsf为坡段内第 f 个隧道的长度 (未在坡段内的部分长度除外)，m；n3为坡段内隧道的数量。

单质点列车力学模型中作用于列车的单位合力为：

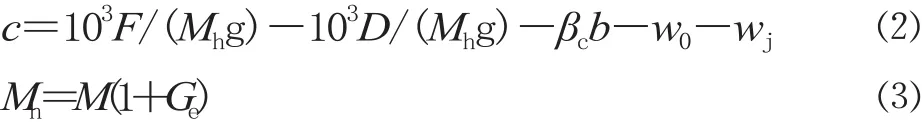
式中：c 为列车的单位合力，N/kN；F 为列车牵引力 (非牵引工况下为 0)，kN；D 为动力制动力 (动力制动不作用时为 0)，kN；b 为紧急制动工况下列车的单位空气制动力 (空气制动不作用时为 0)，N/kN；βc为常用制动系数；w0为列车的单位基本阻力，N/kN；g 为重力加速度，m/s2；Mh为列车的换算质量，t；M 为列车的质量，t；Ge为转动惯量常数。

单质点列车力学模型中的列车运动学方程为[2]：

式中：v1为列车的初速度，km/h；v2为列车的末速度，km/h；Δt 为列车由速度 v1运行到 v2的时间，s；Δs 为列车由速度 v1运行到 v2的距离，m。

2 多质点列车力学模型

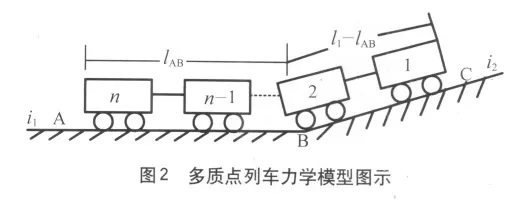
多质点列车力学模型是将每辆车简化成一个质点，构成质点链，能够反映列车编组、长度对受力和运行的影响。多质点列车模型仍以解析法为计算基础，单独计算车辆间的纵向车钩力。如图2 所示，列车的单位加算附加阻力为：

式中：ll为列车的长度，m；lAB为列车在坡段 AB 上的长度，m；i1为坡段 AB 的坡度，‰；i2为坡段 BC的坡度，‰。

公式⑹可视为以lAB为自变量、wj为因变量的函数，该函数为一次初等函数，在整个定义域内连续。wj在过变坡点时是连续变化的。计算列车的运行时分时，车辆间的相互作用是列车的内力，对整个列车加速度的影响可忽略不计。为建模需要将列车简化为质点间无相对运动的质点链。列车所受到的各种附加阻力按长度平均分配，即按列车长度计算平均的加算附加阻力。由于计算机运行速度快，采取的计算步长较小时，每个步长可以随时按列车所覆盖的坡段、曲线和隧道的长度加权平均计算，即按列车所覆盖的地段计算列车所在位置的加算附加阻力[2]。此时，单位加算附加阻力为：

式中：ll为列车长度，m；ik为列车所覆盖的第 k 个坡段的坡度，‰；lk为列车所覆盖的第 k 个坡段的长度，m；Rm为列车所覆盖的第 m 个曲线的半径，m；lqm为列车所覆盖的第 m 个曲线的长度 (未覆盖的部分长度除外)，m；wsf为列车所覆盖的第 f 个隧道的单位附加阻力，N/kN；lsf为列车所覆盖的第 f 个隧道的长度 (未覆盖的部分长度除外)，m；n1为列车覆盖的坡段数量；n2为列车覆盖的曲线数量；n3为列车覆盖的隧道数量。

多质点列车力学模型中第 n 辆车的加速度为：

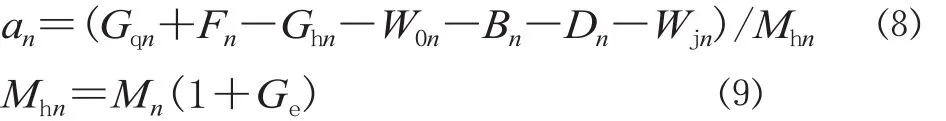
式中：an为第 n 辆车的加速度，m/s2；Gqn为第 n 辆车前车钩拉力，kN；Fn为第 n 辆车的牵引力 (非牵引工况为 0)，kN；Ghn为第 n 辆车后车钩拉力，kN；W0n为第 n 辆车的基本阻力，kN；Bn为第 n 辆车的空气制动力 (空气制动不作用时为 0)，kN；Dn为第 n 辆车的动力制动力 (动力制动不作用时为 0)，kN；Wjn为第 n 辆车的加算附加阻力，kN；Mhn为第 n 辆车的换算质量，t；Mn为第 n 辆车的实际质量，t；Ge为转动惯量常数。

考虑到各辆车的加速度相等：

以每辆车为对象，将公式⑼代入公式⑻中得：

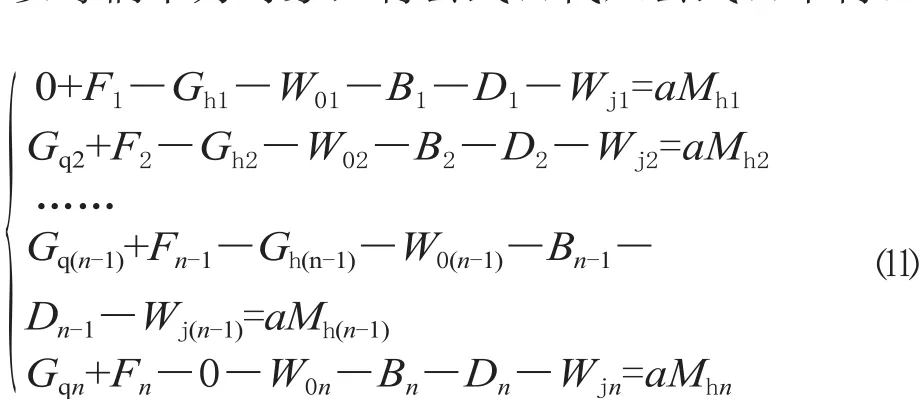
由力的作用是相互的可知：

结合公式 ⑽—公式 ⑿ 得：

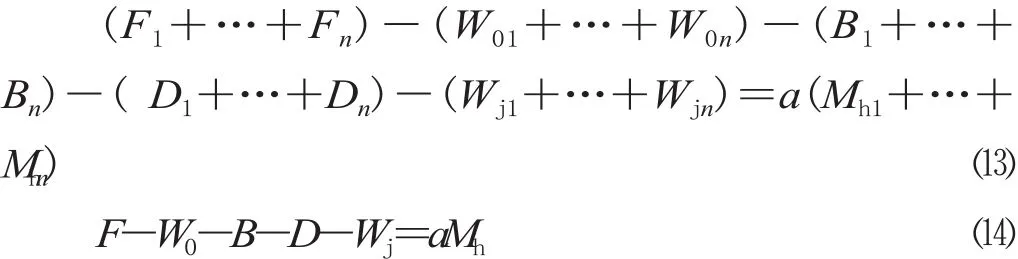
式中：F 为整个列车的牵引力，kN；W0为整个列车的基本阻力，kN；B 为整个列车的空气制动力，kN；D 为整个列车的动力制动力，kN；Wj为列车加算附加阻力，kN。Wj的计算公式为：

由公式 ⒁ 可知，多质点列车力学模型以每一辆车为研究对象，在不考虑列车内部的车辆相对作用时，可将列车视为整体计算列车的合力。由于考虑了列车长度，wj的计算必须采用公式⑺，再结合公式⑵计算单位合力，按照公式⑷、公式⑸计算时间和距离。

3 模型仿真与分析

3.1 仿真条件

列车动力模型仿真选用 SS4型电力机车，牵引滚动轴承重货车 60 辆，牵引质量 4 000 t，高磷铸铁闸瓦，列车的换算制动率为 0.28，列车长 650 m，常用制动列车管减压量 80 kPa，常用制动系数为 0.53，列车管定压为 500 kPa，区间长度为 6.415 km，以时间为迭代变量，迭代步长 0.01 s。线路的纵断面数据和曲线数据如表1 和表2 所示。

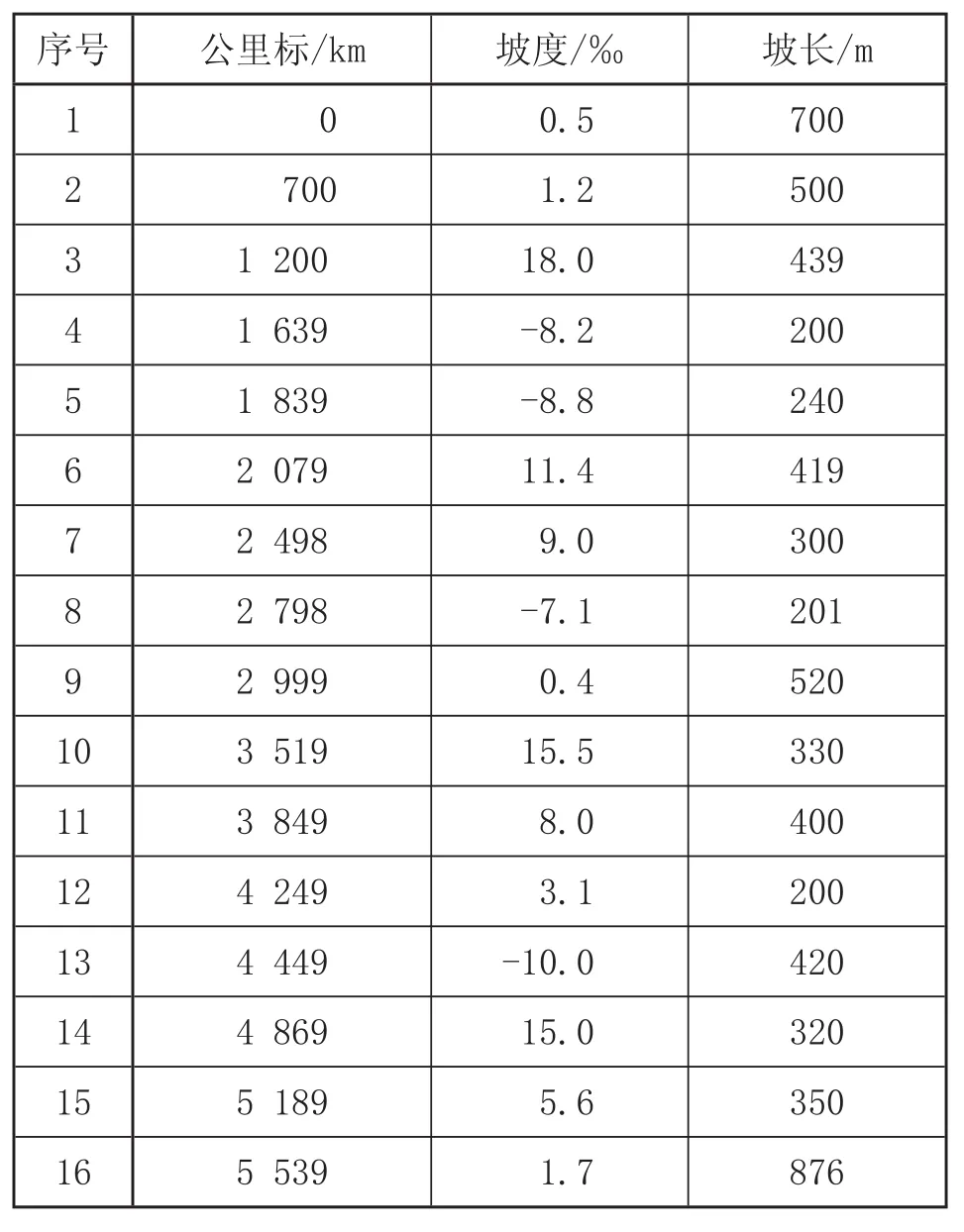
表1 线路的纵断面数据

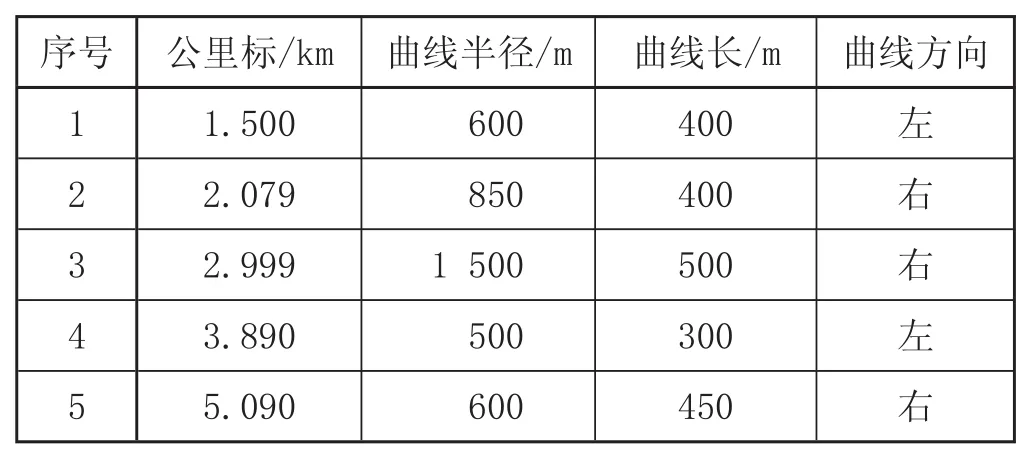
表2 线路曲线数据

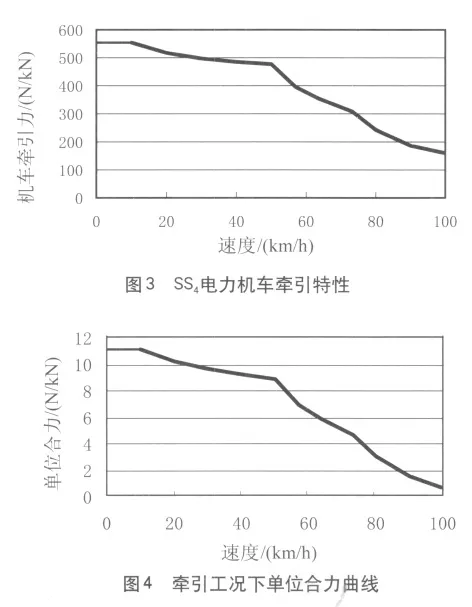
SS4型电力机车的牵引特性如图3 所示，其牵引工况下的单位合力曲线如图4 所示。SS4型电力机车的基本阻力为：

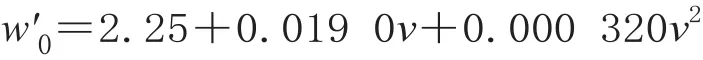
高磷闸瓦的换算摩擦系数为：

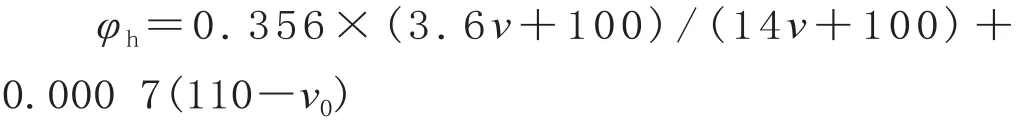
滚动轴承重货车的基本阻力为：

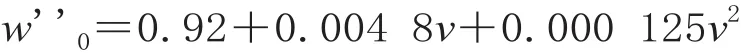
3.2 列车受力分析

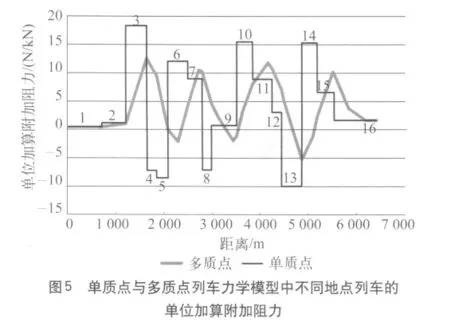
由于隧道附加阻力目前尚无具体的经验公式可循，在仿真中不予考虑。列车在不同地点受到的单位加算附加阻力如图5 所示。在单质点列车力学模型条件下，单位加算附加阻力曲线是间断的，在变坡点发生突变；在多质点列车力学模型条件下，单位加算附加阻力曲线是连续的，随列车的运行距离变化平缓。由上述分析可知，单质点列车力学模型不能如实反映列车单位加算附加阻力的变化趋势。如图5 中，当列车由坡段 10 进入坡段 11 时，单质点列车力学模型中坡度差的绝对值约为 7.5‰，越过变坡点后，单位加算附加阻力以该值发生突变；但是，在多质点列车力学模型中考虑列车长度后，列车由坡段 10 进入坡段 11 时，其单位合力不但没有降低，反而持续上升。当列车由坡段 14 进入坡段15 时亦然。

3.3 仿真结果分析

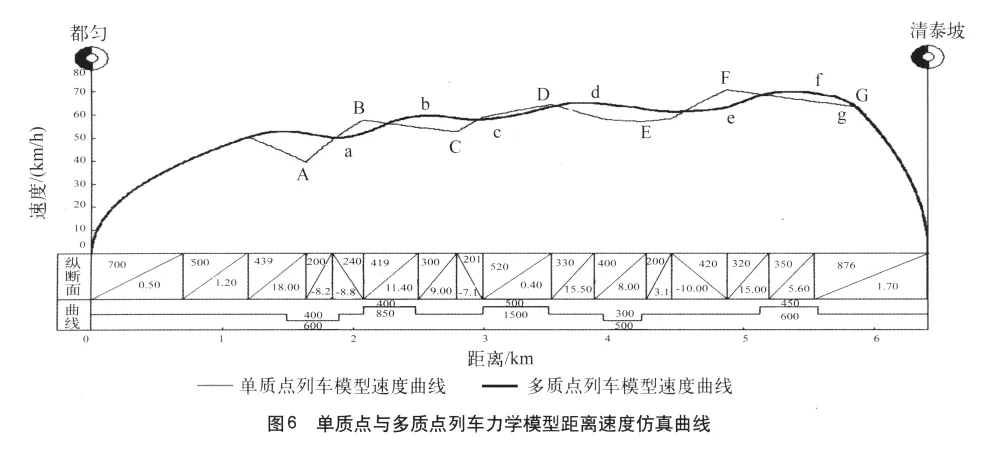
单质点和多质点列车力学模型的距离—速度仿真曲线分别反映了 2 种列车力学模型速度随运行距离的变化，如图6 所示。图6 中的速度曲线显示，多质点列车力学模型条件下，列车的速度变化平缓；单质点列车力学模型条件下，速度在点A,B,C,D,E,F,G处速度波动剧烈，分别由升速转换为减速，或者由减速转换为升速，该类速度趋势的转换点称为速度拐点，在速度拐点处列车的合力为零。图6 中a,b,c,d,e,f,g点为多质点列车力学模型中的速度拐点。单质点列车力学模型中加算附加阻力的突变是导致列车速度剧烈波动的原因；多质点列车力学模型中加算附加阻力的变化是连续的，加速度变化平稳，因此列车速度变化平缓。同时，由于2种不同模型中列车受力的差异，列车速度拐点出现在不同的运行距离上。

在列车起动加速阶段和制动停车阶段，2 种模型的速度曲线拟合程度较高。这是由于车站附近的线路条件较好，同时列车在起动、停车时速度较低，其自身的牵引力或制动力较大，坡段变化对列车速度的影响有限。而在坡度变化较大的区段，列车速度较高，牵引工况下列车的牵引力随速度的升高而降低，惰行工况下基本阻力有所提高；但相对于较大的坡道附加阻力而言，对列车速度产生的影响仍然有限，使2种模型的速度曲线吻合度较低。单质点列车力学模型条件下列车区间运行时分为 514 s，多质点列车力学模型条件下列车区间运行时分为 503 s，绝对误差为 11 s，相对误差约为 3%。

比较 2 种列车力学模型曲线的速度拐点，在进入较大坡度的上坡段时，单质点列车力学模型的列车速度迅速下降，多质点列车力学模型的列车速度变化缓慢。例如，当列车进入 3 号上坡段时，由图6 可知，列车速度约为 50 km/h；由图4 可知，牵引工况下列车单位合力约为 9 N/kN；由图5 可知，单质点列车力学模型的列车加算附加阻力为 18.32 N/kN，并且与列车运行方向相反，因此，列车速度迅速降低。多质点列车力学模型条件下，列车的坡段附加阻力在一段距离内低于 9 N/kN，列车速度上升，但随着列车速度的升高加速度逐渐减小为 0，因此，列车速度变换平缓。同理，可以解释在列车进入坡度较大的下坡段时，单质点列车力学模型中列车速度迅速上升，多质点列车力学模型中列车速度变化缓慢的特点。

4 结论

（1）在计算列车区间运行时分和能耗时，将整个列车视为研究对象，车辆之间的相互作用是列车的内力，对牵引计算的结果影响程度较小，因此，可将列车视为连续的质点链。

（2）建立的数学模型反映了单质点与多质点列车力学模型的本质；两者的外在区别是是否考虑列车长度，本质区别是附加阻力在变坡点的变化是否连续。

（3）多质点列车力学模型较好地考虑了列车长度，附加阻力的变化是连续的；单质点列车力学模型未考虑列车长度，附加阻力在变坡点突变，不符合列车的实际受力过程。

[1]饶 忠. 列车牵引计算[M]. 北京：中国铁道出版社，1999.

[2]张中央，孙中央. 列车附加阻力计算中计入列车长度的辨析[J]. 铁道机车车辆，2000(2)：36-39.

[3]毛保华，何天键，袁振洲，等. 通用列车运行模拟软件系统研究[J]. 铁道学报，2000，22(1)：1-5.