关于二次系统极限环的分布
2010-07-09岳锡亭
岳锡亭, 孙 艳
(长春工业大学基础科学学院,吉林长春 130012)
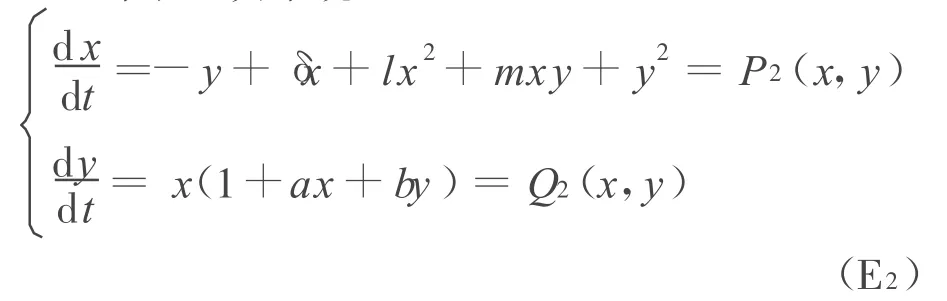
对于二次系统的极限环个数的上界及分布是人们一直关心的问题[1-3],文献[4-5]证明了当系统(E2)的两个奇点D(0,0),N(0,1)分别为粗焦点,且当l≥0,δ(m+δ)>0时,系统(E2)的极限环是集中分布的。对于l<0的情形文中给出以下定理。
定理1 δ(m+δ)+l=0时,(E2)的极限环集中分布。
证明:不妨设δ(m+δ)>0,当δ(m+δ)+l=0时,有
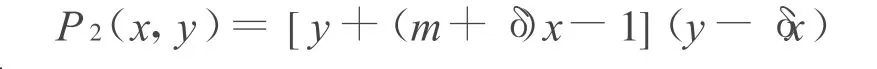
易见,奇点N(0,1)外围的极限环不能与直线y-δ x=0相交。奇点D(0,0)外围的极限环不能与直线y+(m+δ)x-1=0相交。假设奇点N(0,1)外围的极限环为L,沿着N(0,1)外围的极限环L对(E2)的发散量积分有:
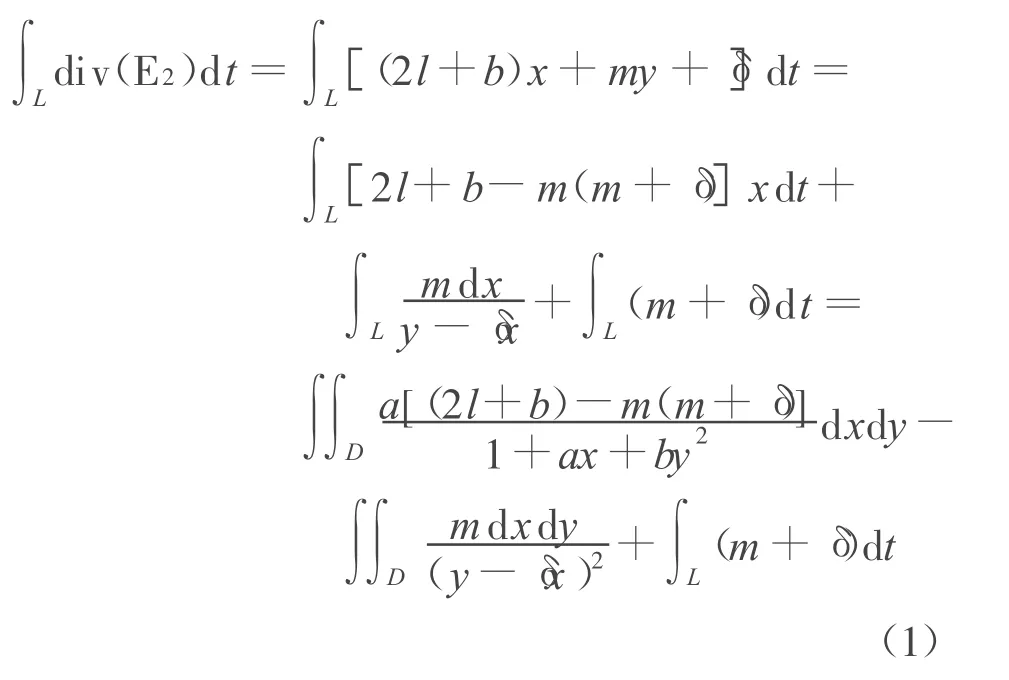
这里D是由L所围成的区域,在应用格林定理时注意到L是顺时针方向的。注意到m+δ=,当l<0时,m+δ与δ的符号相同,且有
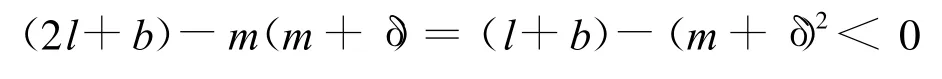
于是,当ma>0,mδ<0时,N(0,1)外围无环。而对于D(0,0)外围的极限环有
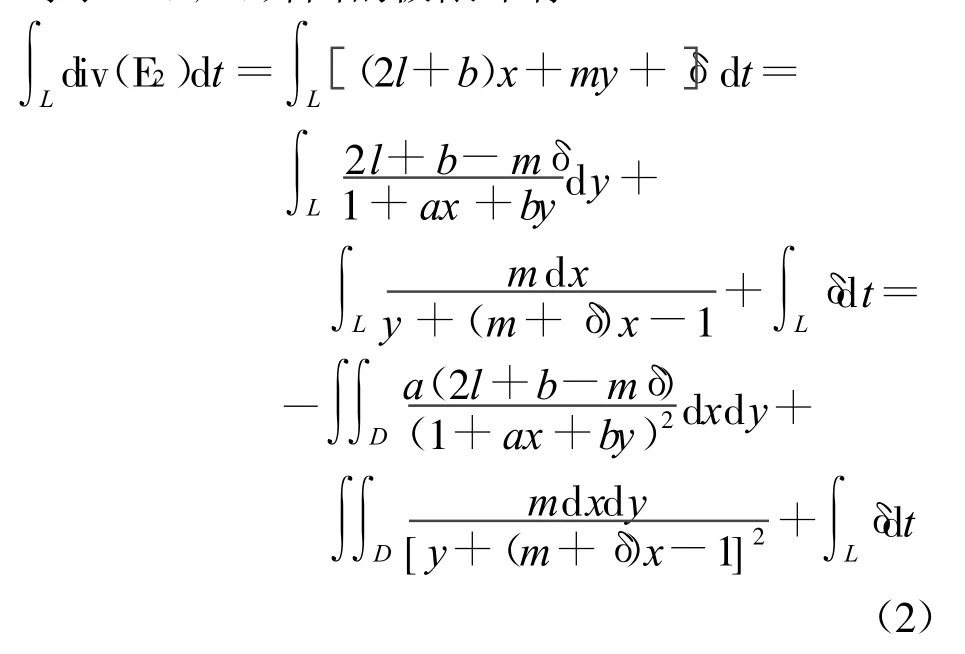
这里L的方向是逆时针方向。于是,当ma>0,mδ≥0时,D(0,0)外围无环。
两者结合,当ma>0,δ(m+δ)+l=0时,(E2)的极限环集中分布。
再由文献[2]的引理2知,ma≤0,δ(m+δ)>0时,(E2)的极限环集中分布知定理1成立。
定理2 当m-bδ=0,δ(m+δ)>0时,系统(E2)的极限环集中分布。
这里依然假设N(0,1)和D(0,0)为粗焦点,且l<0。否则由文献[2]知(E2)的极限环集中分布。
证明:系统(E2)的极限环必然地和发散量为零的直线L:my+(2l+b)x+δ=0相交,并围绕其交点(切触点)于其内部,沿着系统(E2)对发散量为零的直线L求导数,得到方程为:
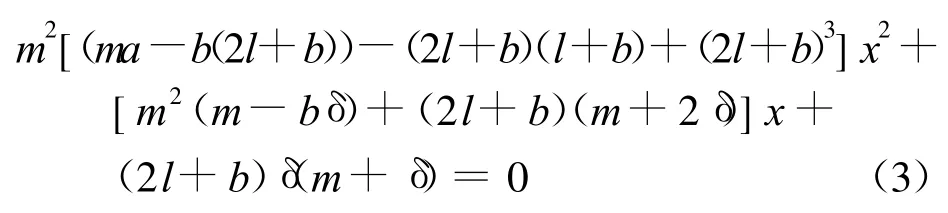
因ma>0,所以假设ma-b(2l+b)<0。否则由文献[2]知其极限环为集中分布,再由m+2δ=(m+δ)+δ的符号与δ的符号相同,于是可知在式(3)中x2项的系数小于零,x项的系数的符号与-δ的符号相同。常数项的符号小于零。所以式(3)若存在根(切触点),则两个根的符号与δ的符号相反,又因直线L:my+(2l+b)x+δ=0与在点处相交,而是无切线。式(3)的两个零点或同时位于直线y=的下方,或同时位于直线的上方,由此知系统(E2)的极限环为集中分布,如图1所示。
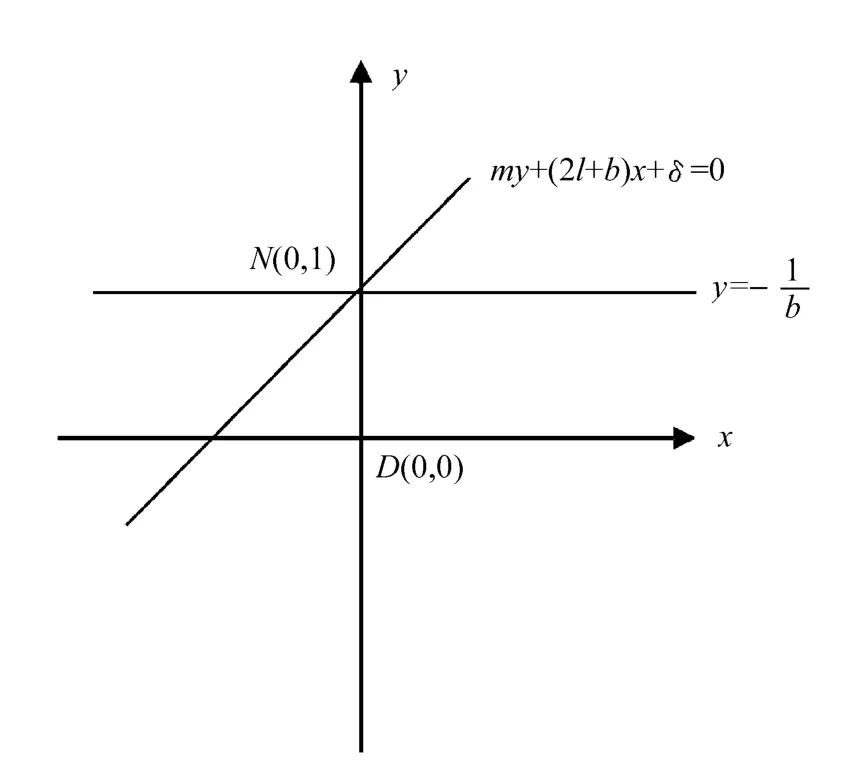
图1 系统(E2)极限环集中分布图
即系统(E2)的极限环只能在一个奇点外围出现。
[1] 叶彦谦.极限环论[M].上海:上海科学技术出版社,1984.
[2] 叶彦谦.多项式微分系统定性理论[M].上海:上海科学技术出版社,1995.
[3] 岳锡亭,闫 丽.关于二次系统极限环的分布[J].东北师大学报:自然科学版,2003,35(1):18-22.
[4] 岳锡亭.一类二次多项式微分系统极限环的分布[J].长春工业大学学报:自然科学版,2002,23(4):55-57.
[5] 岳锡亭.关于二次系统极限环的分布[J].长春工业大学学报:自然科学版,2002,23(1):50-52.
