基于UG装载机构件建模及疲劳寿命分析

张国文，郭维昭

(江西工业工程职业技术学院，萍乡 337055)

0 引言

在可靠性工程中，一个复杂系统往往由大量的分系统或单元组成，而单元是系统的基础，同时系统也可看作是一个单元，因此要研究系统的综合可靠性问题与不同的寿命分布模型。对于机械产品其失效形式主要有结构完整性破坏，包括产品零部件强度降低、断裂破坏、疲劳破坏和磨擦损伤等[1～3]。疲劳破坏是引起产品构件失效的重要原因。疲劳定义为[4]：在某点或某些点承受扰动应力，且在足够多的循环扰动作用之后形成裂纹或完全断裂的材料中所发生的局部的、永久结构变化的发展过程。本文研究了装载机的结构模型及寿命分析模型，对装载机使用可靠性最差的摇臂进行了寿命预算。

1 装载机的结构模型

装载机工作装置主要有以下几部分组成：1铲斗，2连杆，3摇臂，4动臂，5销轴。结构如图1所示。

2 构件疲劳寿命分析模型

图1 装载机工作装置结构

针对构件疲劳失效形式，建立疲劳寿命分析模型。模型结构如图2所示。本文将UG与有限元分析软件结合，进行有限元模型的建立，首先在UG中创建三维实体模型，再将模型以Parasol格式传送给非线性有限元分析软件ABAQUS。进行几何修复后，得到有限元实体模型。

3 使用疲劳寿命预估

图2 疲劳寿命分析模型

疲劳是在循环荷载下，材料局部发生损伤的累积过程。在每一次应力作用下，零件寿命就要受到微量的疲劳损伤，当疲劳损伤积累到一定程度达到疲劳寿命极限时便发生疲劳断裂。利用相似构件在实际载荷谱下的使用理论和损伤的相对Miner理论能进行寿命预测。图3为一零件的规律性非稳定变应力直方图，图中是当循环特性为r时各个循环的最大应力，N1，N2，…Nn为与各应力相对应的积累循环次数。如图4所示为应力—循环次数关系图，N1'， N2',…,Nn'为与各应力对应的材料发生疲劳破坏时的极限循环次数。

图3 规律性非稳定变应力直方图

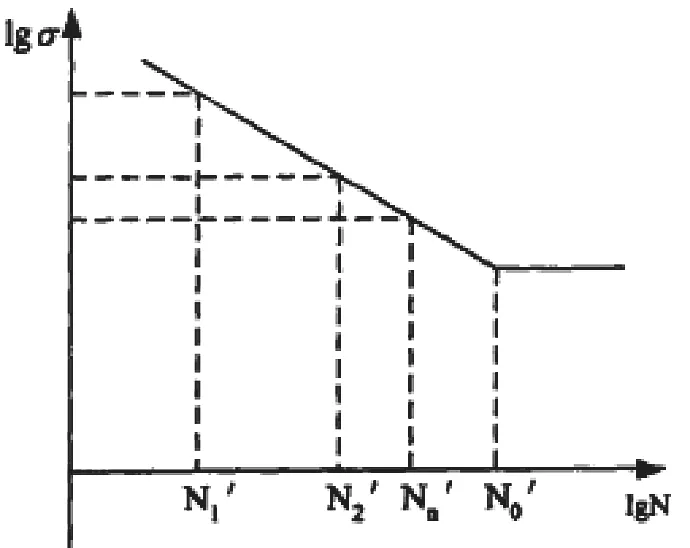
图4 应力—循环次数关系图

Miner线性疲劳损伤积累理论指出:应力每循环一次，造成零件的一次寿命损伤，故其总寿命损伤率：

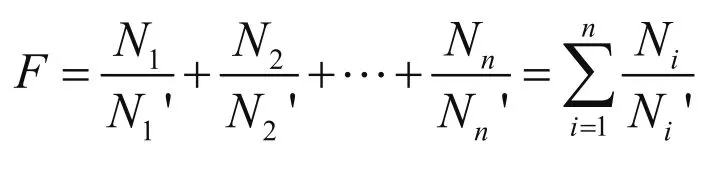
零件达到疲劳极限时，理论上总寿命损伤率为1，即

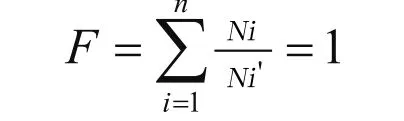
在估算疲劳寿命时，假设认为：应力小于疲劳极限应力 对疲劳寿命无影响。工程机械构件所受应力经试验发现都是随机应力，随机应力的时间历程不能用一个明确的数学关系式来描述和确定在未来某一瞬间的应力准确值，而应用有限元分析软件可以准确得到工作循环随机载荷谱，根据此载荷谱可以进行疲劳寿命预估。首先将载荷转换为当量对称循环应力氏，然后代入疲劳曲线方程式进行求解。根据Goodman疲劳极限图进行计算，计算公式如下[5,6]:

m—指数；

则构件疲劳工作循环次数为：

4 摇臂使用寿命的估算

根据摇臂的实体模型建立有线元模型，材料属性设定：摇臂材料为Q345(16Mn)，弹性模量E=2.07xl011，泊松比µ=0.3。单元类型选择：由于摇臂结构较为复杂，这里采用适应性较好的4节点实体C3D4。边界条件加载：根据装载机工作装置的实际工作状况，约束摇臂销轴内孔平面的X、Y、Z三个方向的自由度。网格划分：设定单元大小并对摇臂模型进行了单元划分。运用ABAQUS进行动态分析，计算得到随时间变化摇臂应力的分布情况，摇臂有限元实体模型如图5所示。

图5 摇臂有限元实体模型

由于载荷方向、大小在不断变化，所以摇臂上不可能有某个点始终处于最大应力状态，但总有一个区域应力处于较高水平。为了数据提取的方便，假设这个区域内有一点A，应力始终处于最大值，如果这一点的强度、寿命等指标达到要求，整个摇臂也就达到要求了。

表1 当量对称循环应力 的计算结果

与当量对称循环应力 和 对应的材料疲劳破坏的极限循环次数分别为：

极限正载工况下摇臂的工作循环次数：

假设装载机每次完成铲掘时间2分钟，每天不间断工作8小时，每年工作300天，这样装载机每年的工作循环次数为72000次，装载机摇臂疲劳失效前的工作时间约为一年零六个月，本实例考虑的是极限正载工况，而在实际工作中，装载机所受外载荷比极限正载时小，但工况较为复杂，包括各种各样的偏载。

5 结论

通过UG与有限元分析软件模型的建立，分析得出：装载机每次完成铲掘时间2分钟，每天不间断工作8小时，每年工作300天，这样装载机每年的工作循环次数为72000次，装载机摇臂疲劳失效前的工作时间约为一年零六个月。

[1] Grant Ireson W,Coombs C.E, Moss R.Y.Handbook of Reliability Engineering and Management[M]. McGraw-Hill.New York,1996.

[2] Doyle R.L.Mechanical-system reliability[J].Tutorial Notes,Annu.Reliability Maintainability Symp,1992.

[3] Chunghun Ha,Way Kuo. Approach for Reliability-Redundancy Allocation Using a Scaling Method[J].Journal of Heuristics,2005,(11):201-217.

[4] 陈传尧.疲劳与断裂[M].武汉:华中科技大学出版社.2002.

[5] 邱宣怀.机械设计[M].北京:高等教育出版社,1997.

[6] 姚卫星.结构疲劳寿命分析[M].北京:国防工业出版社,2004.

[7] 冯秀玲.王永军.杜红英.提高压力机摇摆轴疲劳强度的技术措施[J].锻压装备与制造技术,2006,(5).

[8] 李舜酩.机械疲劳与可靠性设计,2006.

[9] 李哲林.装载机的工作性能分析,2008(3).

[10] 杨先勇.桥式起莺机主梁疲劳寿命研究[D].2005.

[11] 王德俊.疲劳强度设计.中国机械设计大典,2002.

[12] 庄茁,蒋持平.工程断裂与损伤,2004.

[13] 《机械工程材料性能数据手册》编委会.机械工程材料性能数据手册,1994.

[14] 魏良模,朱新榕,孙友松,魏航.变速驱动曲柄压力机运动分析[J].锻压装备与制造技术,2004,(3).